DotDyn
介绍
RotDyn类主要用于处理单个轴的转子动力学问题,通常需要借助Commonshaft类一块使用。
原理
转动动力学方程$^{[1]}$
考虑转动效应的动力方程如下:
$$
[M]{\ddot{u}}+([G]+[C]){\dot{u}}+([K]-[K_{\mathfrak{c}}]){u}={F}
$$
式中:$[M],[C],[K]$一一分别为结构质量、阻尼和刚度矩阵;
$\left[K_{\mathrm{c}}\right]$一结构转动引起的旋转软化矩阵,它使旋转坐标系下的结构刚度降低;$[G]$一结构转动对“阻尼”矩阵的贡献,在旋转坐标系下通常称为科氏矩阵或科氏阻尼矩阵,而在固定坐标系下称为回转矩阵或回转阻尼矩阵;$[F]$一—固定坐标系下的外荷载向量。在旋转坐标系下,为外荷载向量与科氏力向量之和,科氏力向量$\langle F_{\mathrm{c}}\rangle=[G]\langle\dot{u}\rangle_{0},,\langle\dot{u}\rangle_{0}$为命令IC定义的节点速度向量。
从上式中,不难看出影响一个结构的响应主要影响在于质量、阻尼、刚度,如何获得准确的结构的相关信息,是得到准确计算的关键。
在旋转坐标系下,转动效应称为科氏效应,即生成科氏矩阵和科氏力。科氏矩阵通过转速和单元形函数求得各单元的科氏矩阵,然后累加形成结构的科氏矩阵。科氏力则为科氏矩阵与节点速度之积。
在固定坐标系下,转动效应称为回转效应,即生成回转矩阵,它通过单元回转动能和单元形函数求得。在转子动力学中,将回转效应分为两部分,即与转速相关的回转矩阵和与位移相关的回转矩阵,只是动力学方程表达形式不同而已。
在ANSYS中,无论考虑回转效应或是考虑科氏效应均采用命令CORIOLIS定义。
质量参数$^{[2]}$
首先结构的质量参数,应该在网格构建完成后便知晓,下文介绍了如何通过网格来计算结构的质量,转动惯量等参数。
设有一个旋转对称体,Ox 轴为其旋转对称轴。 图1为通过旋转轴 Ox 的半平面截取此物体得到的截面轮廓图。我们在轮廓线上取 N 个点, 使得连接这些点形成的封闭折线,尽可能地逼近轮廓线。从这些点中任选一点为起点,按顺时针方向绕轮廓线顺次把这些点编号为 1、2,直到 N。

折线中的每一线段,以Ox为轴旋转一周,构成一个截头圆锥台。我们先分别计算每一圆锥台的惯性参量;然后,再按一定的规则,把各个圆锥台的惯性参数综合在一起,就得到整个旋转体的惯性参量。
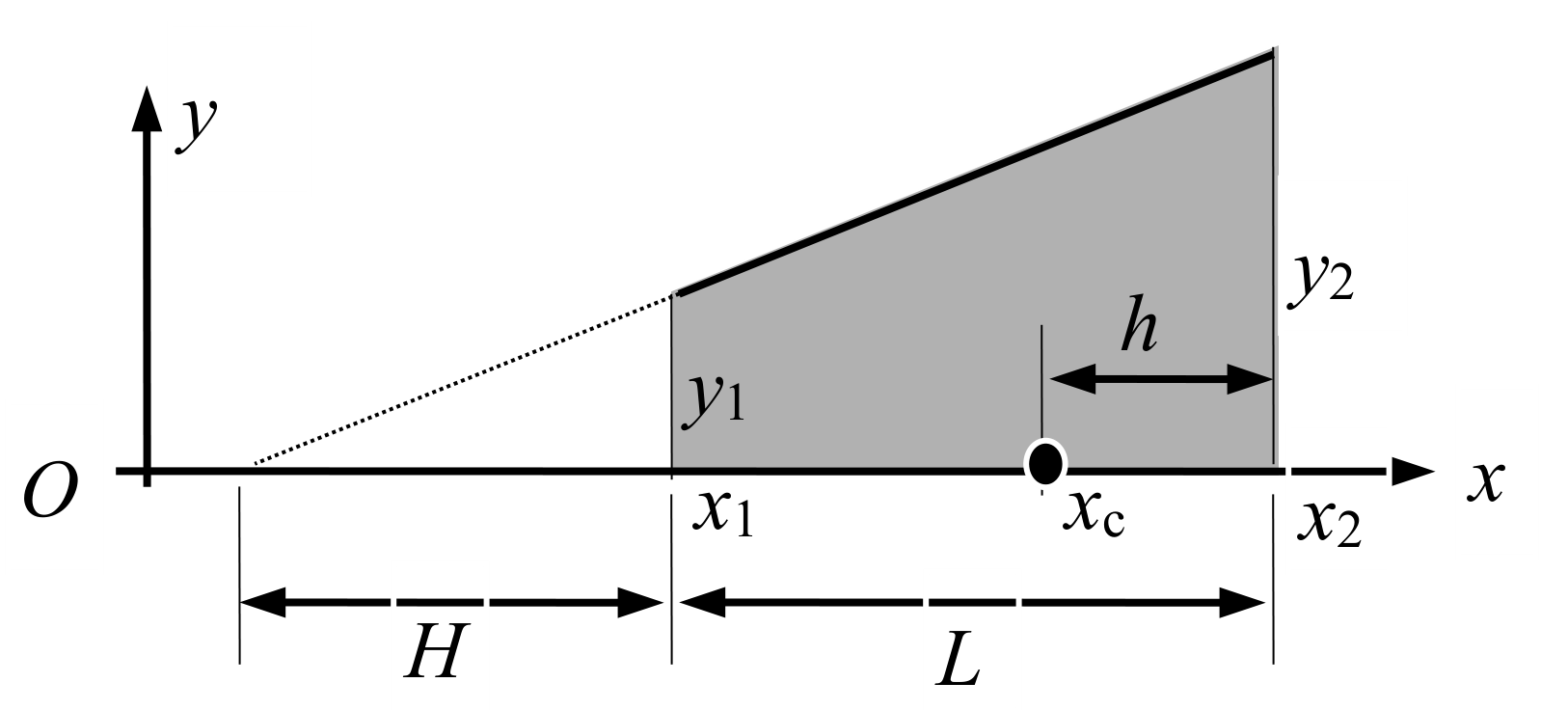
一个圆锥台是计算惯性参数中的基本单元,设其母线两端点的坐标为x1,y1和x2,y2。由理论力学中知识,不难得到,该圆锥台的惯性参量为:
质量:
$$
M=\frac{1}{3}\pi\rho Ly_1^2\frac{\alpha^3-1}{\alpha-1}
$$
质量中心:
$$
x_c=x_2-\frac{L}{4}\frac{\alpha^2+2\alpha+3}{\alpha^2+\alpha+1}
$$
绕x轴的转动惯量:
$$
J_x=\frac{1}{10}\pi\rho Ly_1^4\frac{\alpha^5-1}{\alpha-1}
$$
绕中心直径的转动惯量:
$$
J_{xc}=\pi\rho(L+H)y_2^2[\frac{y_2^2}{20}+\frac{(L+H)^2}{80}+\frac{(\frac{L+H}{4}-h)^2}{3}]-\pi\rho Hy_1^2[\frac{y_1^2}{20}+\frac{H^2}{80}+\frac{(L+\frac{H}{4}-h)^2}{3}]
$$
式中,
$\rho$ — 密度,
$\alpha$ — $y_2/y_1$,
$H$ — $Ly_1/(y_1+y_2)$,
$h$ — $\frac{L}{4}\frac{\alpha^2+2\alpha+3}{\alpha^2+\alpha+1}$,
圆柱是一个特殊的圆锥台,有y1=y2,它相应的惯性参量为
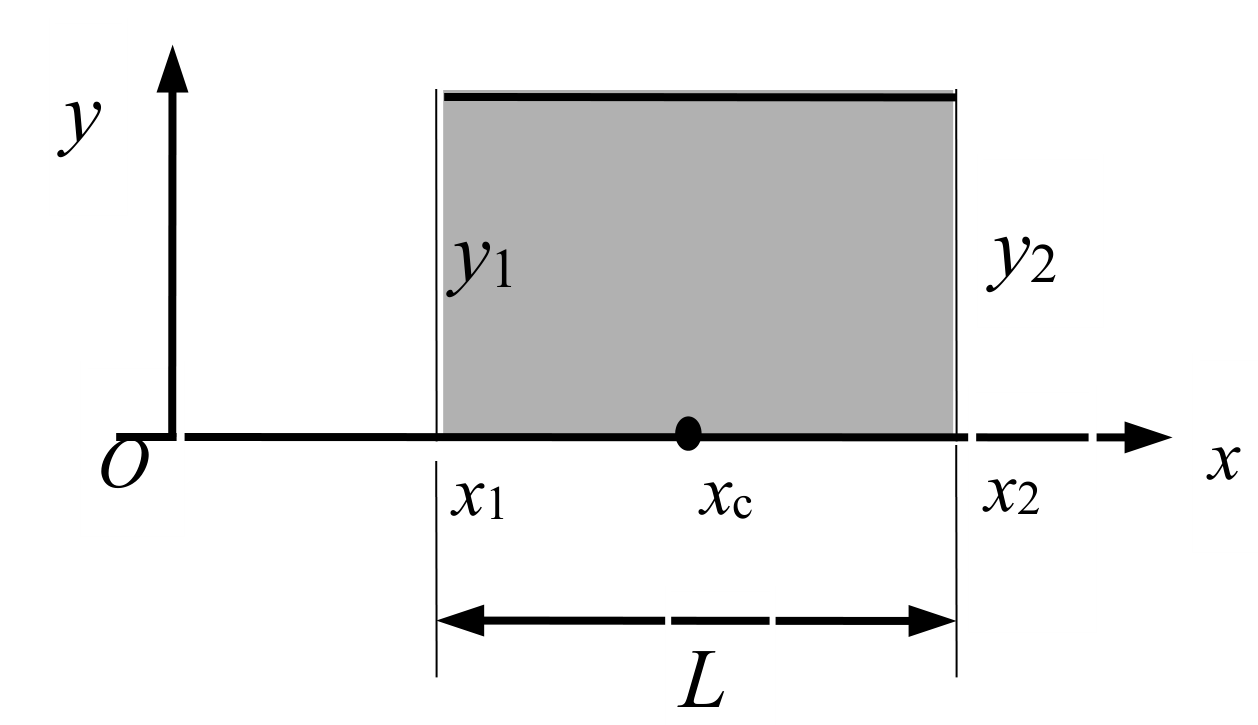
质量:
$$
M=\pi\rho Ly_1^2
$$
质量中心:
$$
x_c=0.5(x_1+x_2)
$$
绕x轴的转动惯量:
$$
J_x=\frac{1}{2}\pi\rho Ly_1^4
$$
绕中心直径的转动惯量:
$$
J_{xc}=0.25\pi\rho Ly_1^2(y_1^2+\frac{L^2}{3})
$$
对于编程,首先,我们可以得到任意形状的截面网格,从而通过上述方法得到结构的转动惯量参数。
- 整体的质量和极转动惯量取各个圆锥台的相应量的代数和;
- 将各圆锥台质心,平行力系合成规则得到整体的质心;
- 用移轴定理求出各个圆锥台对过公共质心的直径转动惯量,然后代数相加得整体的直径转动惯量。
以一个半径50mm的钢球举例($\rho =7850kg/m^3$) , 其理论计算的公式如下 :
质量:
$$
M=\frac{4}{3}\pi\rho R^3=4.11kg
$$
绕x轴的转动惯量:
$$
J_x=\frac{2}{5}MR^2=4.11kg·m^2
$$
绕y轴的转动惯量:
$$
J_y=\frac{2}{5}MR^2=4.11kg·m^2
$$
理论计算和程序计算对比结果如下:
| Items | Theory | Program | Error |
|---|---|---|---|
| Mass | 4.11 | 4.06 | 1.02% |
| $J_x$ | 4.11 | 4.06 | 1.02% |
| $J_y$ | 4.11 | 4.06 | 1.02% |
有一个半径50 mm , 长度200mm的轴体 , 其理论计算公式如下:
质量:
$$
M=\pi\rho R^2L=12.3kg
$$
绕x轴的转动惯量:
$$
J_x=\frac{1}{2}MR^2=15.374t·mm^2
$$
绕y轴的转动惯量:
$$
J_y=\frac{1}{4}MR^2+\frac{1}{12}ML^2=48.685kg·m^2
$$
理论计算和程序计算如下,两者基本一致。
| Items | Theory | Program | Error |
|---|---|---|---|
| Mass | 12.3 | 12.3 | 0% |
| J_x | 15.374 | 15.374 | 0% |
| J_y | 48.685 | 48.685 | 0% |
阻尼参数
在ANSYS中可使用7种阻尼,即Rayleigh阻尼、材料阻尼、常阻尼比、模态阻尼、单元阻尼、材料常阻尼系数、材料结构阻尼系数。在ANSYS结构动力分析中,仅在VT法谐响应分析中可采用滞变阻尼模型,库仑阻尼模型可用于瞬态动力分析,其他均采用黏性阻尼模型。在ANSYS中可同时指定多种阻尼,程序自动形成阻尼矩阵,但不是所有阻尼均可用于各种动力分析。各种分析类型可用阻尼见下表。从表中可知,动力分析类型不同,其所能够定义的阻尼类型也不同,而不同的阻尼类型在ANSYS中的输人命令亦不相同,因此在定义阻尼时应引起足够的重视。
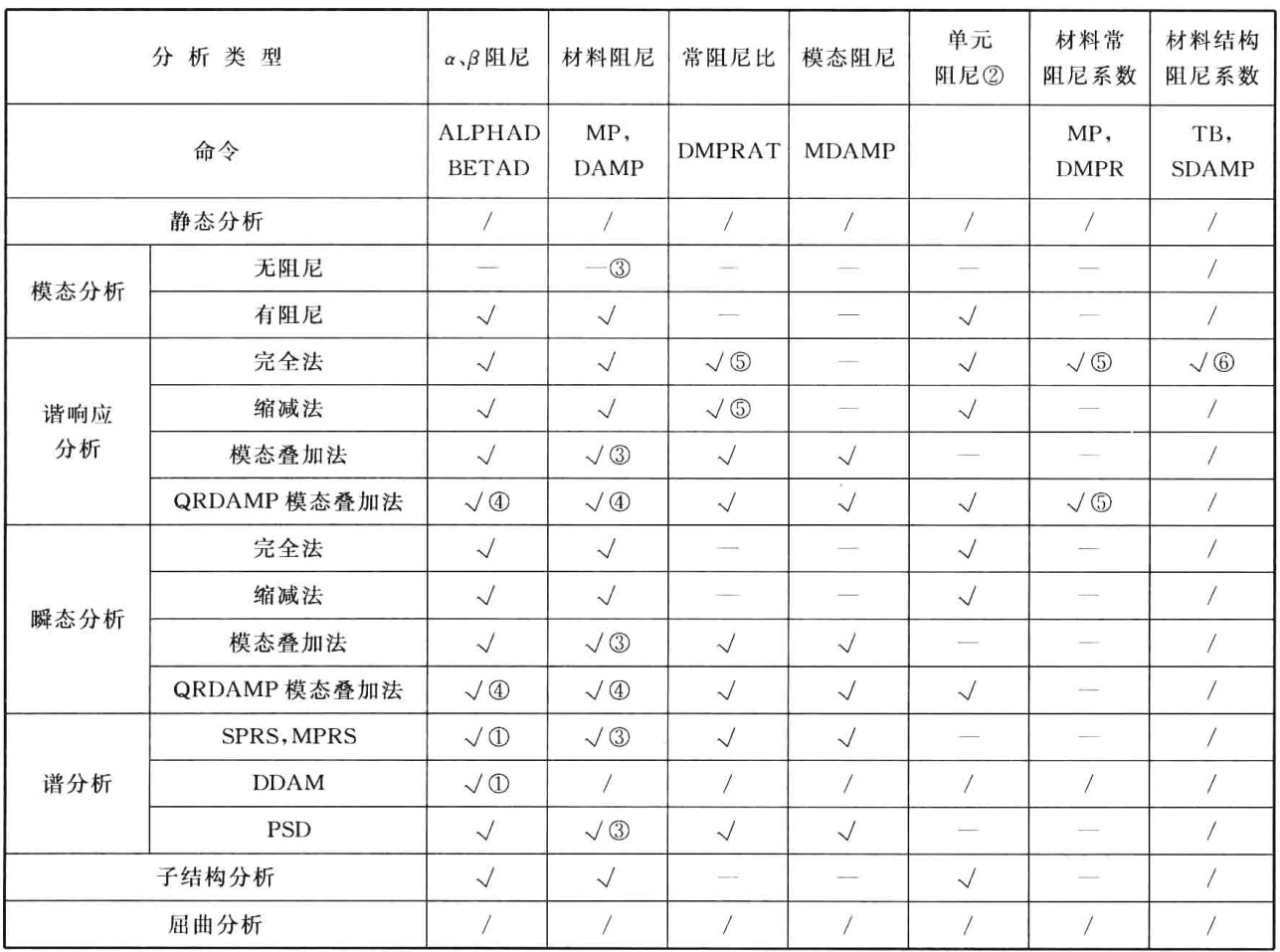
注:1.表中“/”表示不需要,“”不考虑,“$\sqrt{}$”可考虑。2.$①$仅可用$\beta$阻尼,$,\alpha$阻尼不可用;$②$包括超单元阻尼矩阵;$③$“MP,DAMP”定义等效材料阻尼比,用于后续的谱分析或模态叠加法分析;$④$在模态叠加法中,必须采用QRDAMP法提取模态才可考虑$\alpha$阻尼$\mathcal{S}$阻尼和材料阻尼(MP,MADP);$⑤$在谐响应分析中,命令DMPRAT和“MP,DMPR”定义的是结构阻尼比,而非模态阻尼比;$⑥$必须用命令“TB,ELAS”定义材料性质。
在 Baffalo RotDyn中设置params.Damping为常阻尼比。
常阻尼比(ConstantDampingRatio)是定义结构阻尼的最简单方法,也就是通常简称的阻尼比$\xi$一一实际阻尼与临界阻尼之比,采用命令DMPRAT定义。常阻尼比仅适用于谐响应分析、谱分析和模态叠加法瞬态动力分析。
对于材料阻尼DAMP、材料常阻尼系数DMPR和材料结构阻尼系数SDAMP可在对应的材料里设置。
材料常阻尼系数(ConstantMaterialDampingCoefficient)仅适用于谐响应分析的完全法和QRDAMP模态叠加法,采用命令“MP,DMPR”定义。
材料结构阻尼系数是频变阻尼,采用命令“TB,SDAMP”和TBFIELD定义,仅用于变分法谐响应分析,并可选择黏性阻尼模型或滞变阻尼模型。
针对单元阻尼,可以在Support中设置,RotDyn会将其转换为combin14单元和combin214单元来计算。
Support’% Spring connected to ground
% Node number,kx,K11,K22,K12,K21,Cx,C11,C22,C12,C21
刚度参数
部件的刚度比如齿轮、轴承、联轴器均有相关的规范和计算方法,可以参考其他部件Baffalo说明。
频响函数
频响函数 ( Frequency Response Function, FRF) , 它是结构的输出响应和 输入激励力之比,频响函数 FRF 具有以下性质:
频响函数定义为输入位置单位激励力引起的输出位置的响应。
频响函数是系统的固有特性, 与系统本身有关, 与激励、 响应等外界因素没有关系。
频响函数具有互易性, 即 Hij = Hji, 也就是说, j 点单位激励力在 i 点引起的响应等于 i 点单位激励力在 j 点引起的响应, 这也表明频响函数矩阵是对称的。
频响函数是复值函数, 因而其可以用幅值与相位或者实部与虚部表示, 故而频响函数 具有幅频、 相频和实频、 虚频等多种表现形式。”
在RotDyn中设置params.Type=1可设置频响函数分析。
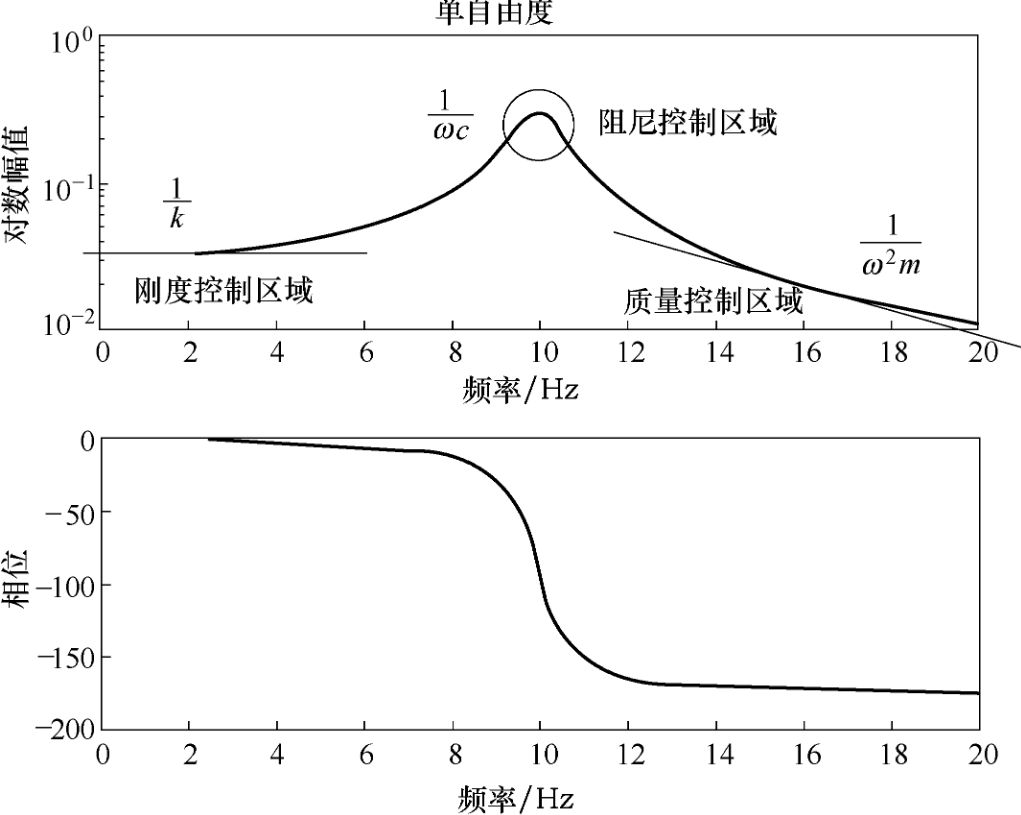
单自由度频响函数
以单自由度的频响函数为例,
“在 低 频 段, FRF 的 幅 值 是 1 / k( k >> ω2 m + jωc) , 相 位 为 0, 表明共振频率以下的频率段主要 用占主导地位的刚度项来描述。
在 高 频 段, FRF 的 幅 值 为 - 1 / ω2 m( ω2 m >> jωc + k) , 相 位 为 - 180°, 表明共振频率以上的 频率段主要用占主导地位的质量 项来描述。
理论上, 无阻尼固有频率处 的 FRF 幅值应是无穷大, 但是由 于阻尼的存在, 导致共振频率处 的幅 值 不 会 无 穷 大, 其 幅 值 为 1 / ωc, 相位突变 180°, 表明在共振频率处主要受阻尼控制。
AMRotor
RotDyn的时序分析和PID控制,主要基于开源转子动力学分析软件AMrotor
类结构
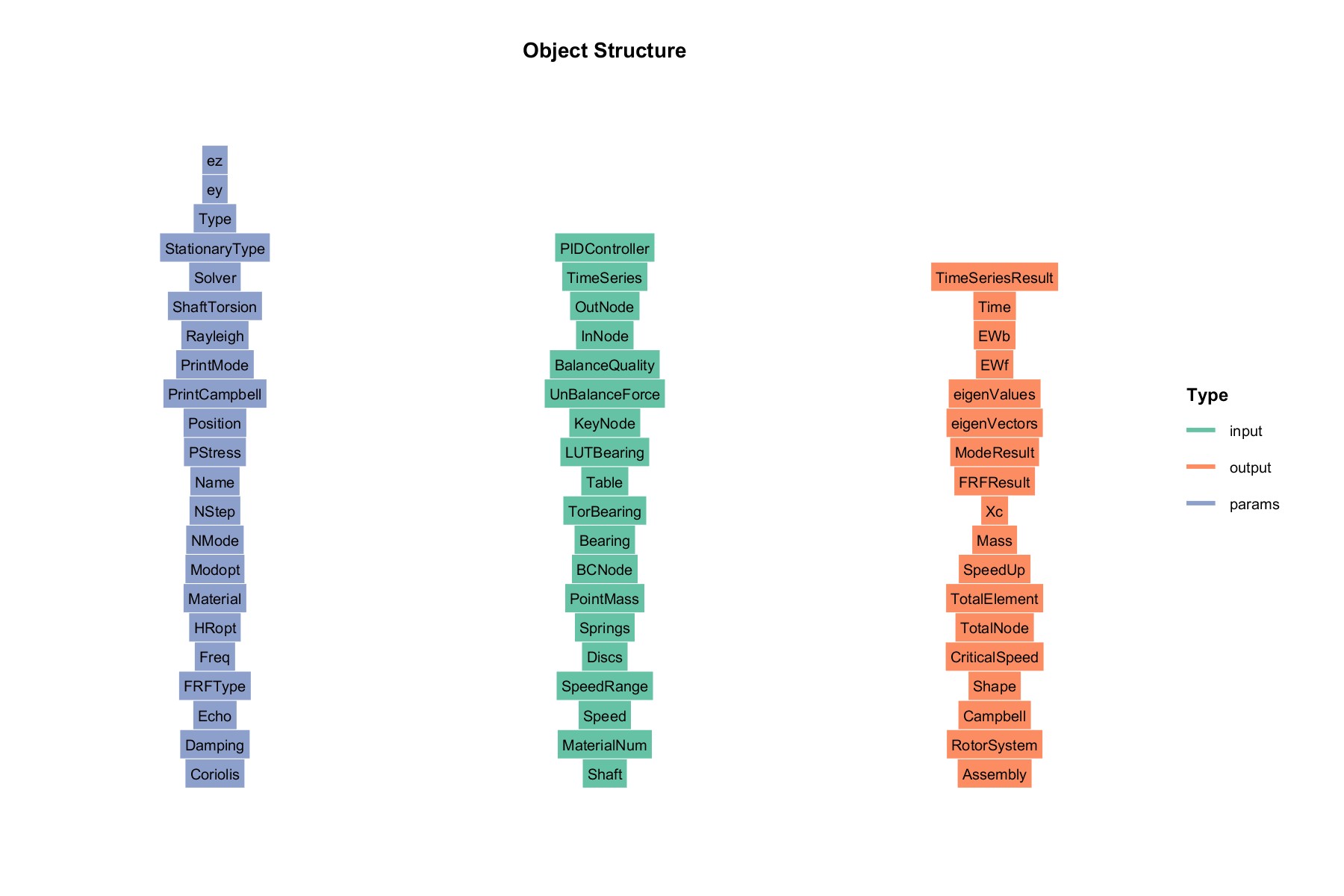
输入 input:
- BalanceQuality : 动平衡质量
- UnBalanceForce : 不平衡量me
- KeyNode : 关键点
- BCNode : 边界点
- PointMass : 附加的节点质量
- Discs : 附加转盘
- Speed : 计算转速
- MaterialNum : 材料编号
- Shaft : 轴
- PIDController : PID控制器
- TimeSeries : 时序
- LUTBearing : 刚度随转速变化轴承
- Table : 轴承刚度和阻尼map
- TorBearing: 转动方向的轴承
- Bearing : 轴承包含刚度和阻尼参数
- SpeedRange : 升速分析的转速范围
参数 params:
- ez :z向偏心
- ey : y向偏心
- Type : 求解类型 Type=1 FRF分析;Type=2 模态计算;Type=3为谐响应分析;Type=4 定转速时序分析;Type=5 s升速或降速时序分析
- Rayleigh : 瑞利阻尼
- PrintMode :输出模态图
- PrintCampbell : 输出坎贝尔图
- Position : 轴位置
- PStress : 考虑预应力
- Name : 名称
- NStep :计算步数
- NMode : 模态数
- Modopt : 模态计算方法
- HRopt: 谐响应计算方法
- Material : 材料
- Freq : 频率计算范围
- Damping : 阻尼比
- Coriols : 科式力
输出 output :
- Xc : 轴重心位置
- TimeSeriesResult : 时序分析结果
- Time : 时间序列
- Ewb : 负进动
- Ewf : 正进动
- eigenValue : 模态分析幅值
- eigenVector :模态分析方向
- ModeResult : 模态分析结果
- FRFResult :FRF分析结果
- Mass : 轴质量
- SpeedUp : 加速曲线
- TotalElement : 总的单元数
- TotalNode :总的节点数
- CriticalSpeed : 临界转速
- Shape : 轴形状
- Campbell : 坎贝尔图数据
- Assembly : 轴装配
案例
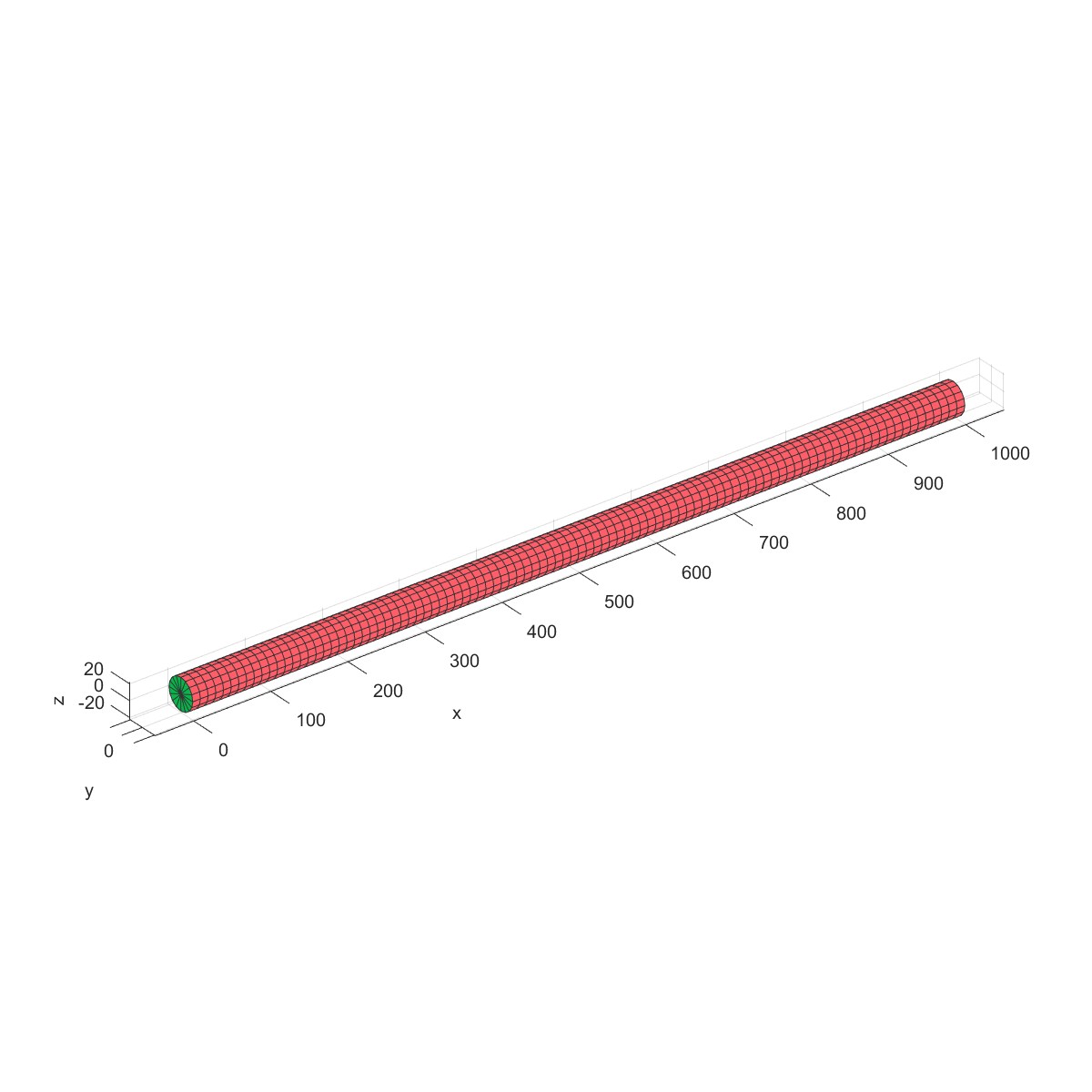
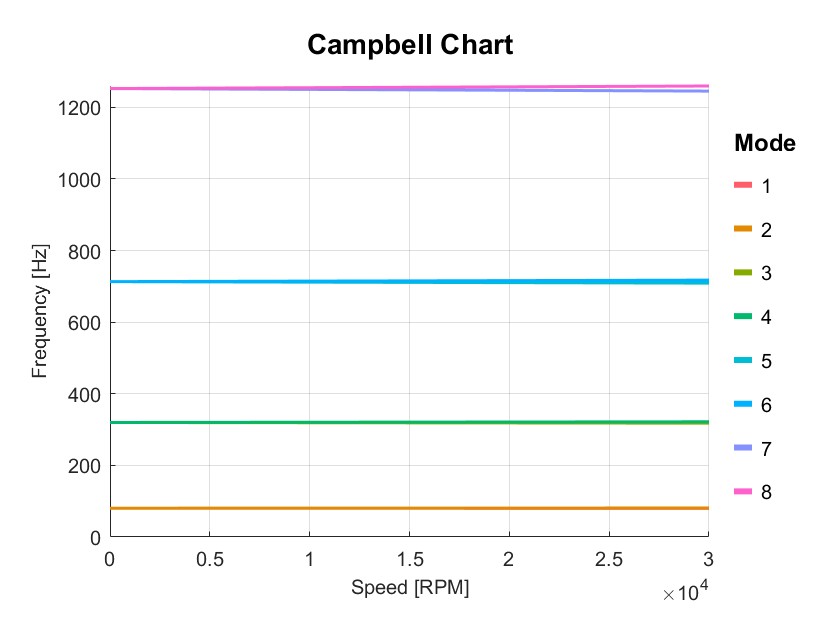
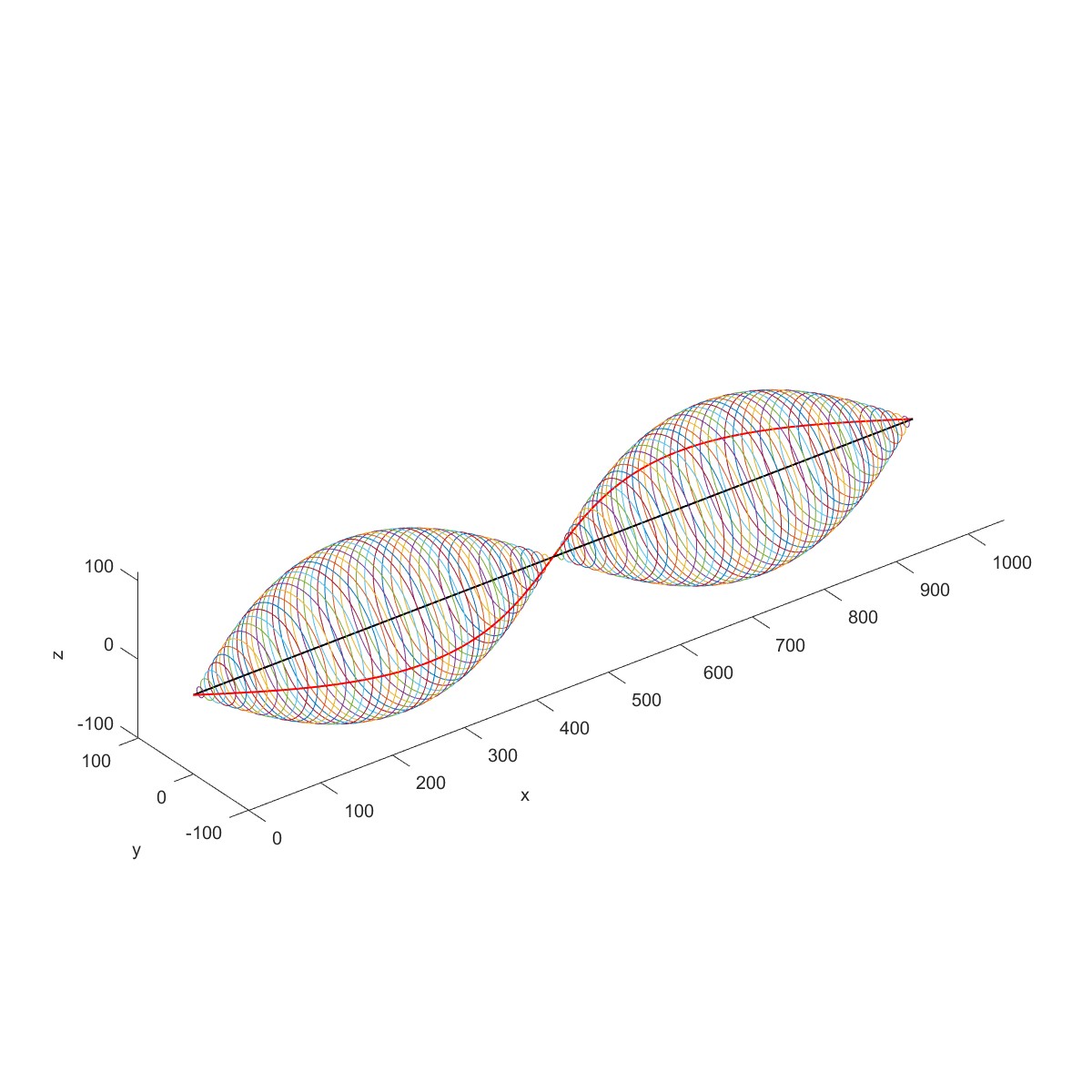
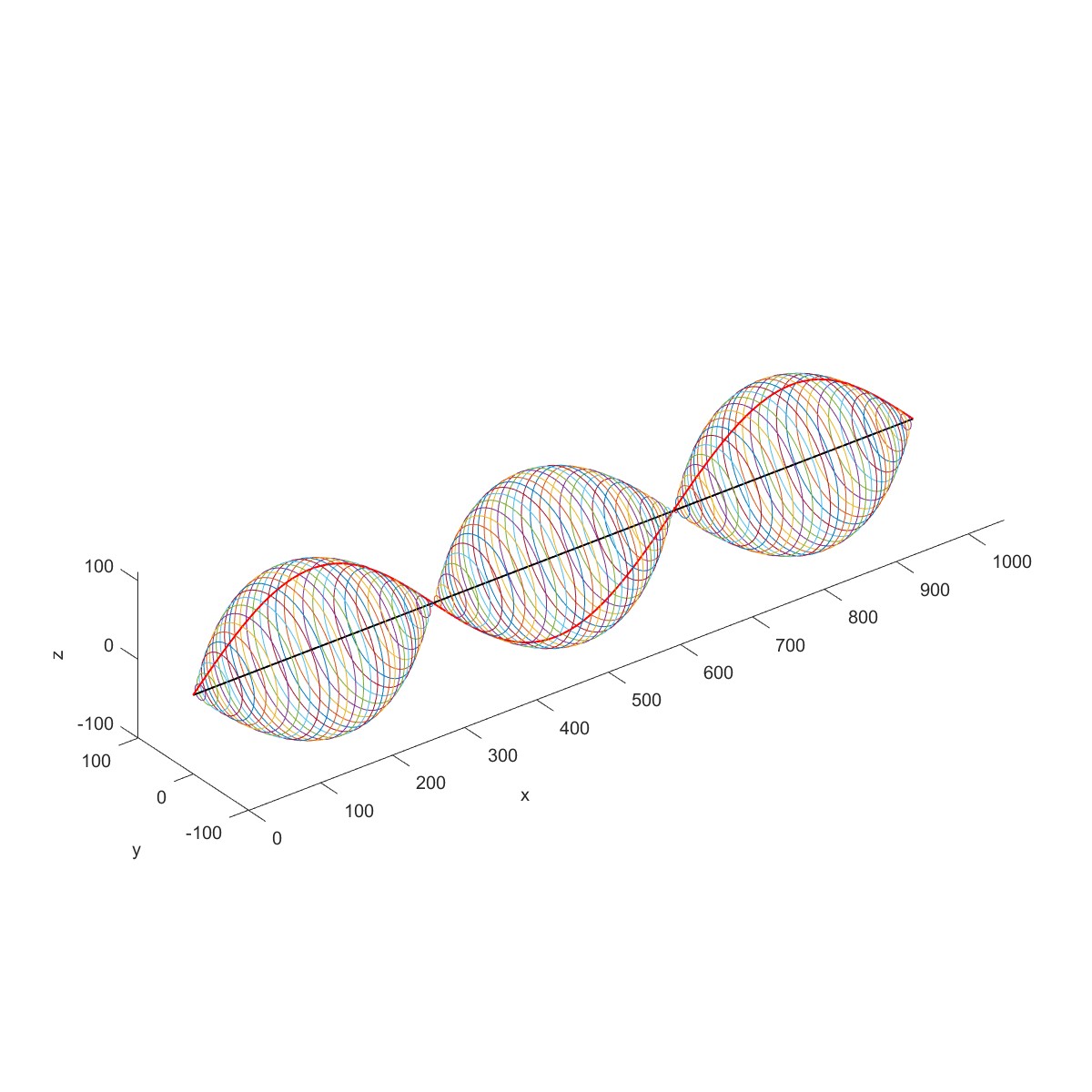
Shaft modal analysis (Flag=1)
下图为一个等截面转子,长 l 为 1m,圆形截面的直径 d=0.04m,两端为简支支承。转子材料的质量密度 为 7800kg/m 3 ,弹性模量 E 为 2.0×10 11 N/m 2 。求此转子在静止状态下的固有频率。
此转子的各阶固有圆频率 $\omega i$ 有理论解如下:
$$
\omega_i=i^2\pi^2\sqrt{\frac{EJ}{\gamma Al^4}}
$$
以截面惯性矩 $J=πd^4 /64$,截面积 $A=πd^2 /4$,固有频率 $f= \omega/2π$ 代入,得到转子的各阶固有频率 $f_i$为
$$
f_i=\frac{i^2\pi}{8}\frac{d}{l^2}\sqrt{\frac{E}{\gamma}}
$$
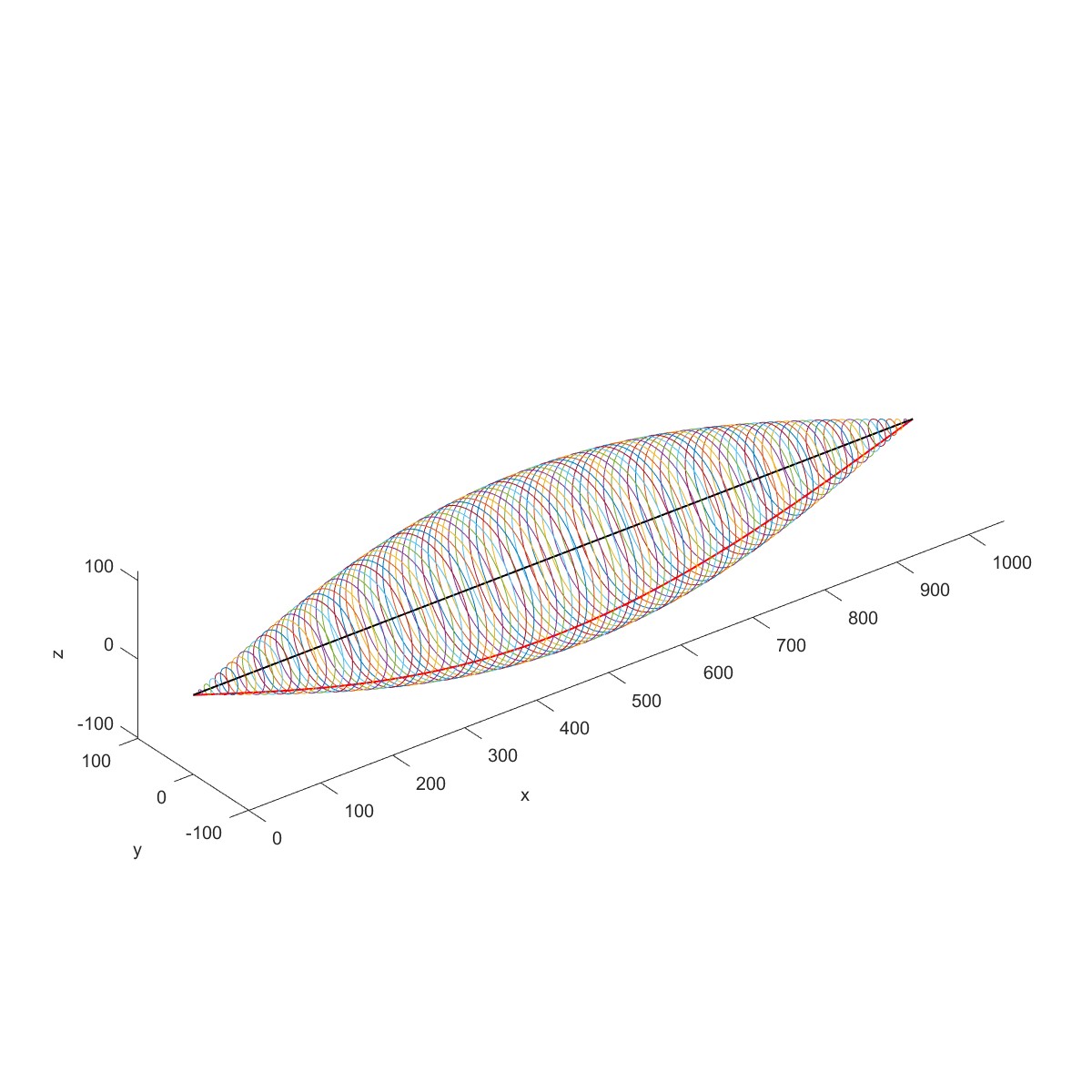
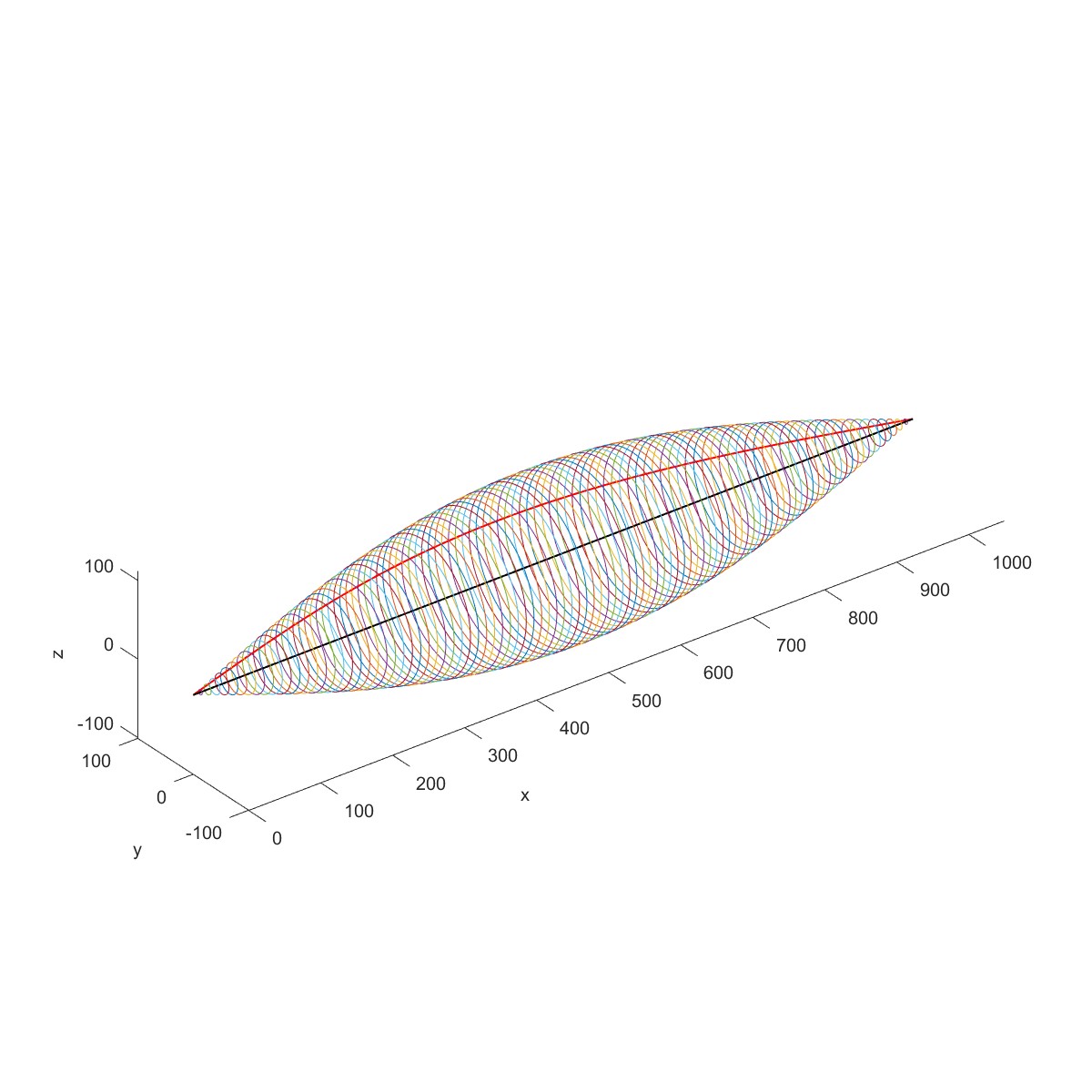
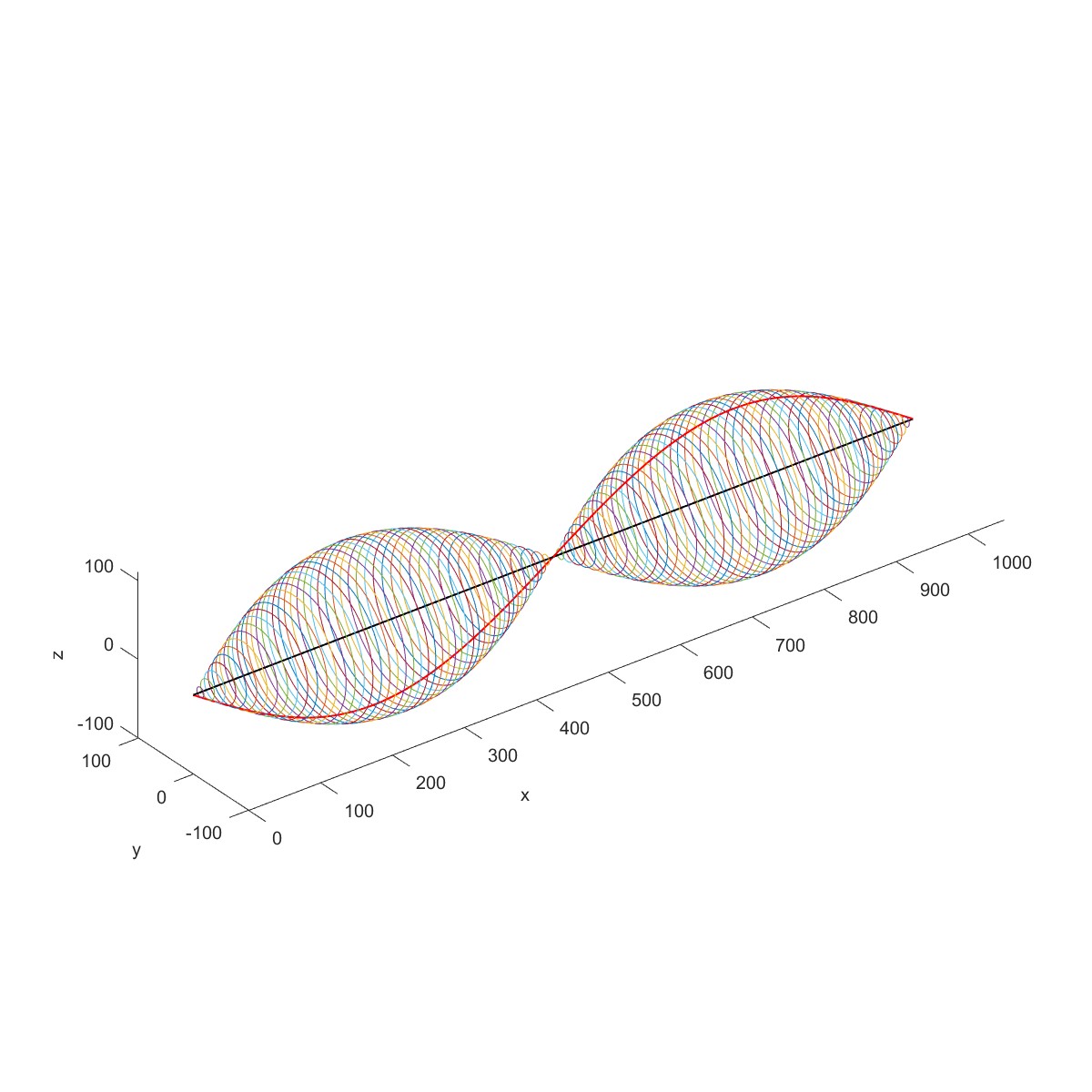
代入具体数据,得到前 3 阶固有频率为 79.5403、318.1612、715.8627Hz,相应的振型为半个周期、一个周期和一个半周期的正弦曲线。
% Shaft 1
inputshaft1.Length = 1000;
inputshaft1.ID = [0,0];
inputshaft1.OD = [40,40];
paramsshaft1 = struct();
obj1 = shaft.Commonshaft(paramsshaft1, inputshaft1);
obj1 = obj1.solve();
mat{1,1}=obj1.params.Material;
inputRotDyn.Shaft=obj1.output.BeamMesh;
inputRotDyn.Speed=[0,15000,30000];
inputRotDyn.MaterialNum=1;
inputRotDyn.BCNode=[1,1,1,1,0,0,0;size(obj1.output.Node,1),0,1,1,0,0,0];
paramsRotDyn.Material=mat;
paramsRotDyn.PrintCampbell=1;
paramsRotDyn.PrintMode=1;
paramsRotDyn.Freq=[0,3000];
obj2 = solve.RotDyn(paramsRotDyn,inputRotDyn);
Plot(obj2);
obj2 = obj2.solve();
ANSYSSolve(obj2.output.Assembly)
obj2=PlotCampbell(obj2,'NMode',8);
for i=1:10
PlotMode(obj2,2,i,'scale',10)
end
 |  |
 |  |
 |  |
 |  |
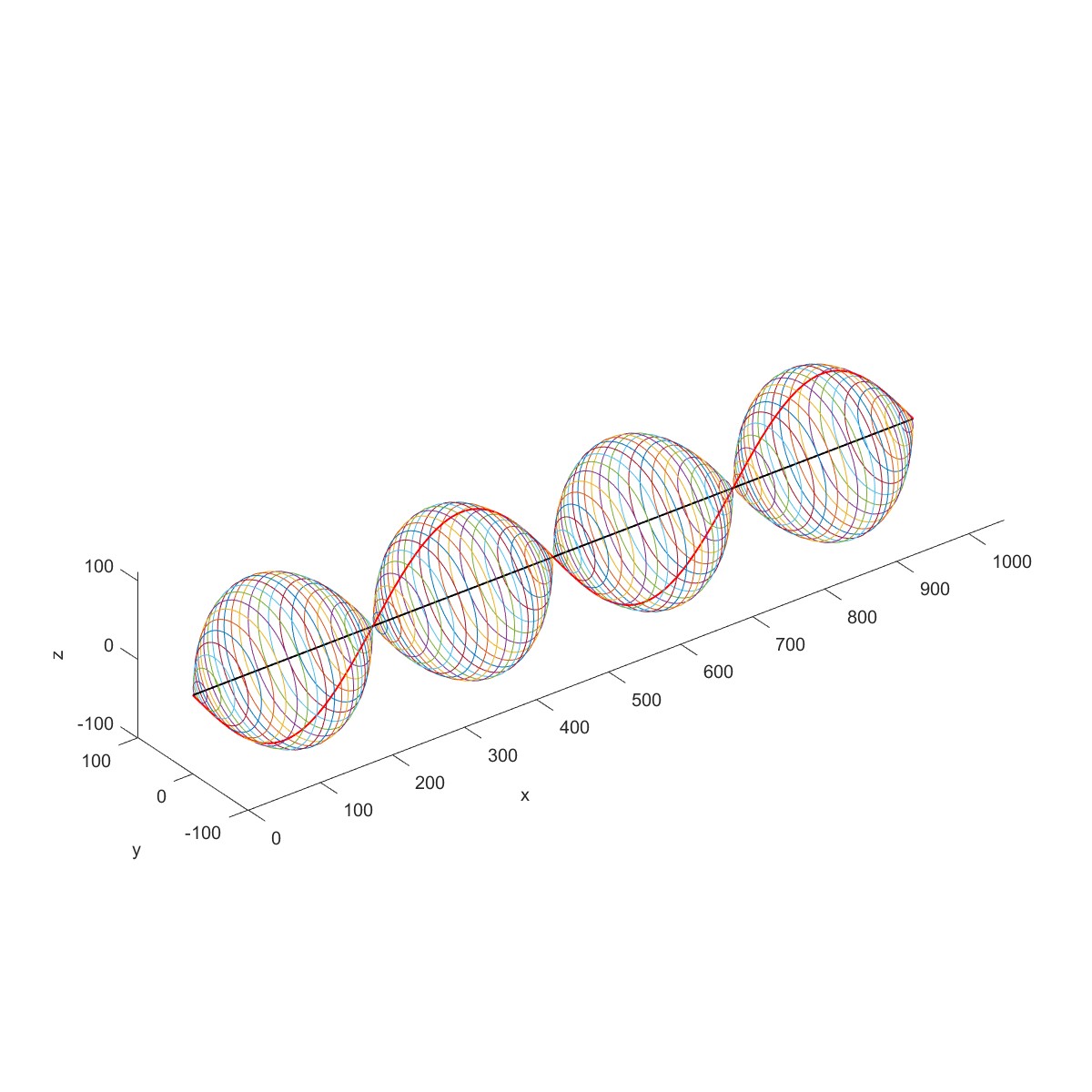 | 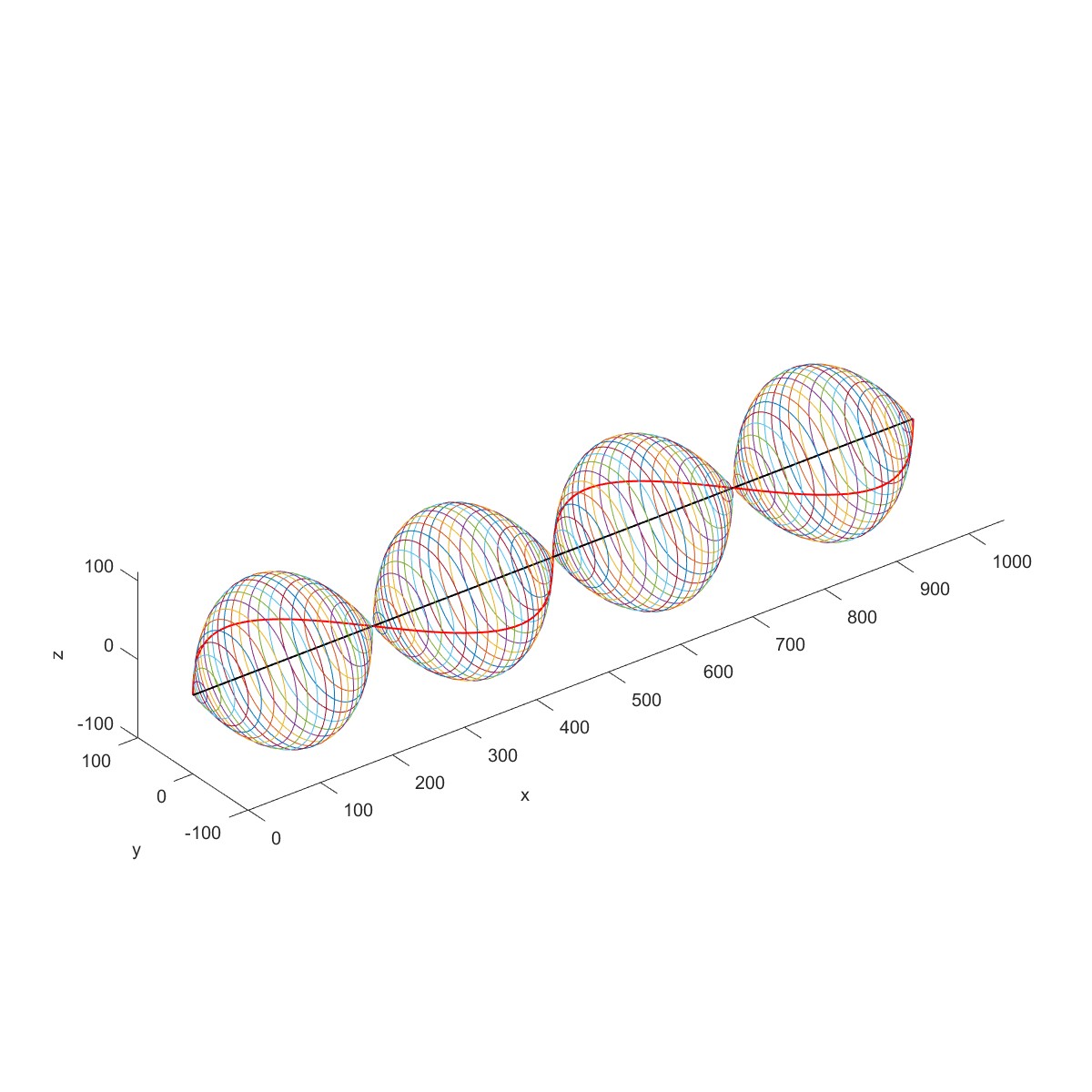 |
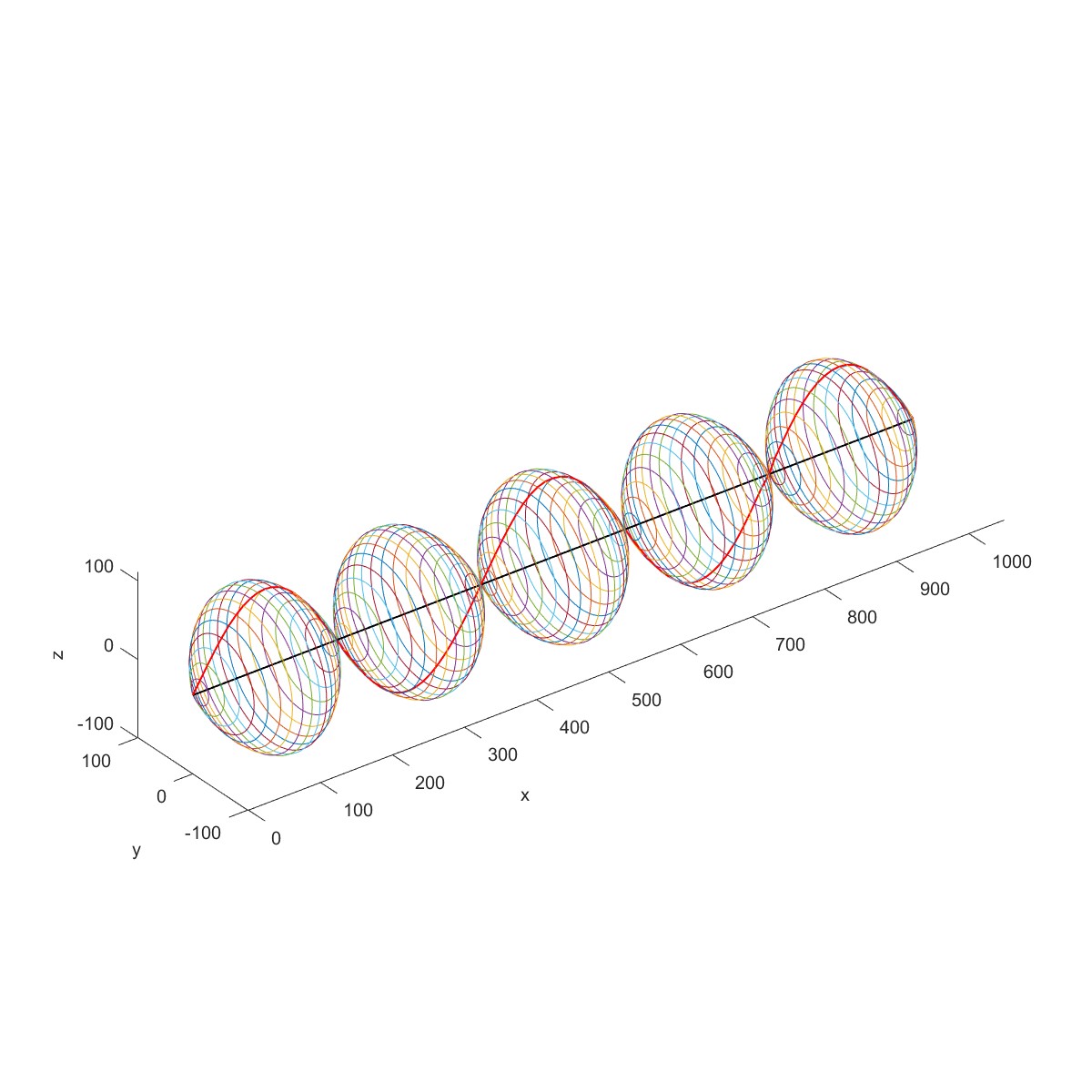 | 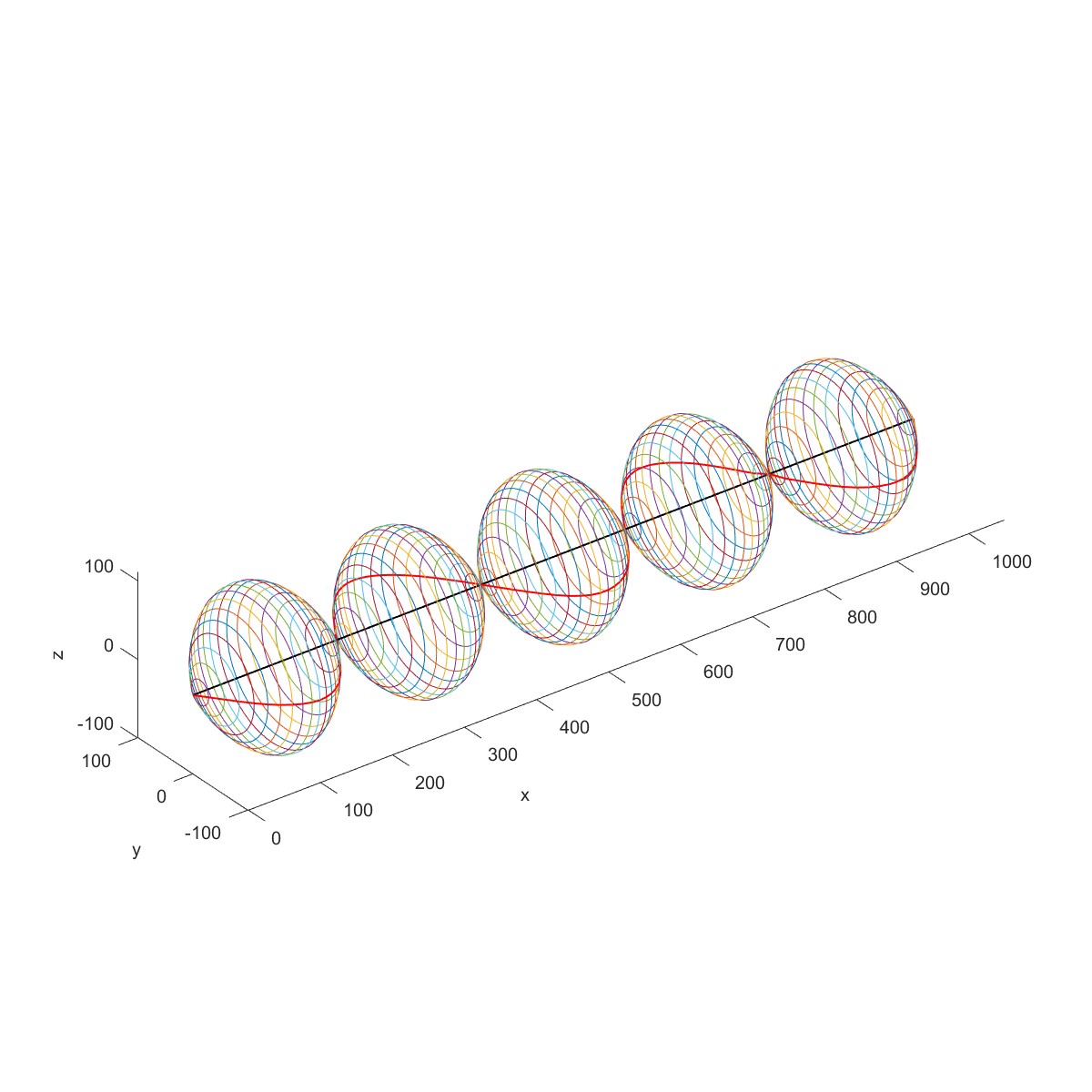 |
Add Discs (Flag=2)
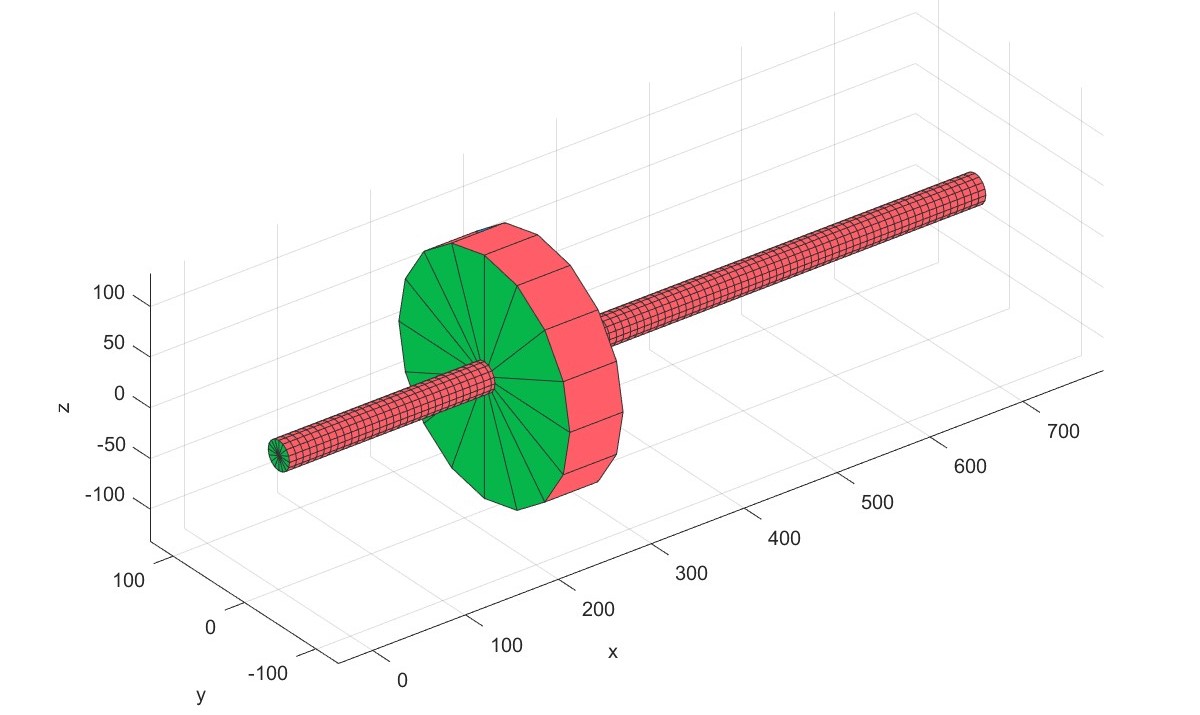
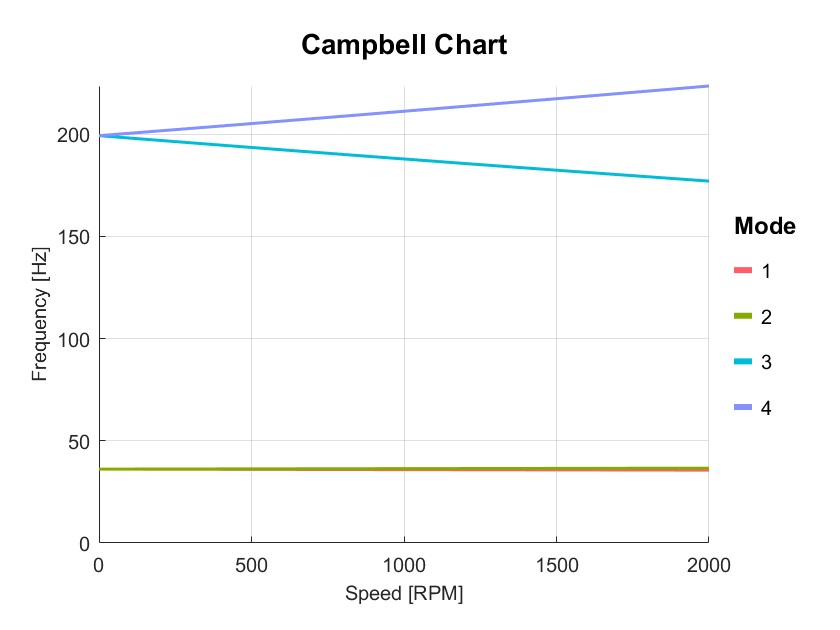
如图所示的刚性支承单圆盘转子,圆盘的质量$m=20kg$,半径$R=120mm$,转轴的跨度$l=750mm$,直径$d=30mm$。圆盘到左支点的距离$a=l/3=250mm$。
仅考虑轴的弯曲但不计轴的质量,考虑回转效应时的频 率方程为:
$$
\omega^{4}-2\Omega\omega^{3}-21340661 \times 10^{6}\omega^{2}+17674781\times10^{6}\Omega\omega+1~2052387 \times 10^{11}=0
$$
其中,$\varOmega$为转速(即激励),$\omega$为待求涡动频率,两者单位均为rad/s。
ID=30;
inputshaft1.Length =750;
inputshaft1.ID = [0,0];
inputshaft1.OD = [ID,ID];
paramsshaft1.Beam_N = 16;
obj1 = shaft.Commonshaft(paramsshaft1, inputshaft1);
obj1 = obj1.solve();
mat{1,1}=obj1.params.Material;
inputRotDyn.Shaft=obj1.output.BeamMesh;
inputRotDyn.Speed=[0,400,800,1200,1600,2000];% Unit: RPM
inputRotDyn.MaterialNum=1;
inputRotDyn.BCNode=[1,1,1,1,0,0,0;size(obj1.output.Node,1),1,1,1,0,0,0];
paramsRotDyn.Material=mat;
paramsRotDyn.PrintCampbell=1;
paramsRotDyn.Position=[0,0,0,0,0,0];
Dyn = solve.RotDyn(paramsRotDyn,inputRotDyn);
[Dyn,Num1]= AddCnode(Dyn,250);
DiscMass=20*10^-3;
rou=obj1.params.Material.Dens;
OD=240;
L=DiscMass/((OD^2-ID^2)*pi/4*rou);
Dyn= AddDisc(Dyn,Num1,OD,ID,L,1);
Plot(Dyn);
Dyn = Dyn.solve();
ANSYSSolve(Dyn.output.Assembly)
PlotCampbell(Dyn,'NMode',4);
Add Userdefined Disc, output moment of inertia (Flag=3)
OD=30;
inputshaft1.Length =750;
inputshaft1.ID = [0,0];
inputshaft1.OD = [OD,OD];
paramsshaft1.Beam_N = 30;
obj1 = shaft.Commonshaft(paramsshaft1, inputshaft1);
obj1 = obj1.solve();
mat{1,1}=obj1.params.Material;
inputRotDyn.Shaft=obj1.output.BeamMesh;
inputRotDyn.Speed=[0,1500,3000];% Unit: RPM
inputRotDyn.MaterialNum=1;
inputRotDyn.BCNode=[1,1,1,1,0,0,0;size(obj1.output.Node,1),1,1,1,0,0,0];
paramsRotDyn.Material=mat;
paramsRotDyn.PrintCampbell=1;
paramsRotDyn.Position=[0,0,0,0,0,0];
Dyn = solve.RotDyn(paramsRotDyn,inputRotDyn);
[Dyn,Num1]= AddCnode(Dyn,250);
[Dyn,Num2]= AddCnode(Dyn,500);
a1=Point2D('Circle center');
a1=AddPoint(a1,0,0);
a1=AddPoint(a1,[-50;50],[0;0]);
b1=Line2D('Semi circle');
b1=AddCircle(b1,50,a1,1,'ang',180);
b1=AddLine(b1,a1,2);
S1=Surface2D(b1);
a2=Point2D('Square corner');
a2=AddPoint(a2,[-100;-100;100;100],[0;50;50;0]);
b2=Line2D('Square');
b2=AddCurve(b2,a2,1);
S2=Surface2D(b2);
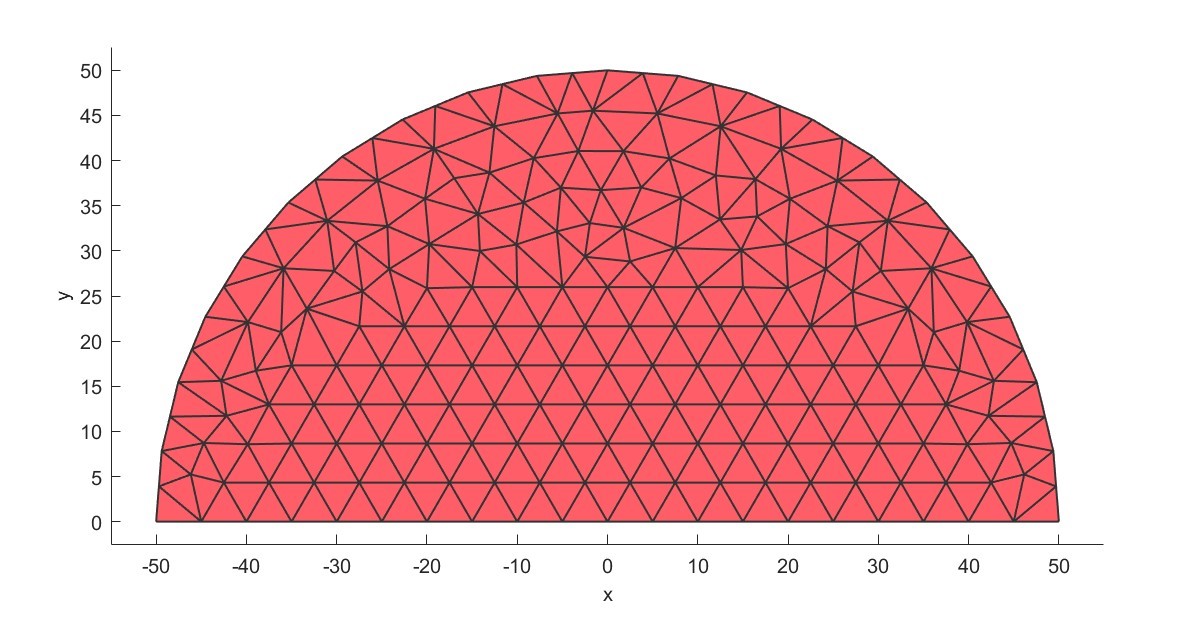
Dyn= AddUserdefinedDisc(Dyn,Num1,S1,1);
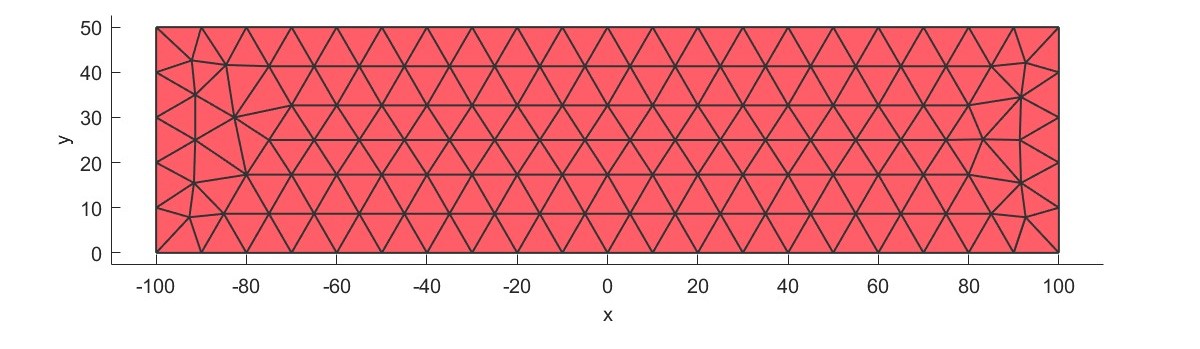
Dyn= AddUserdefinedDisc(Dyn,Num2,S2,1);
Plot(Dyn);
disp(Dyn.input.PointMass)
加入自定义的截面并计算其质量、转动惯量和弯曲惯量。
Successfully revolve to solid mesh .
35.0000 0.0041 4.0578 4.0580
69.0000 0.0123 15.3742 48.6848
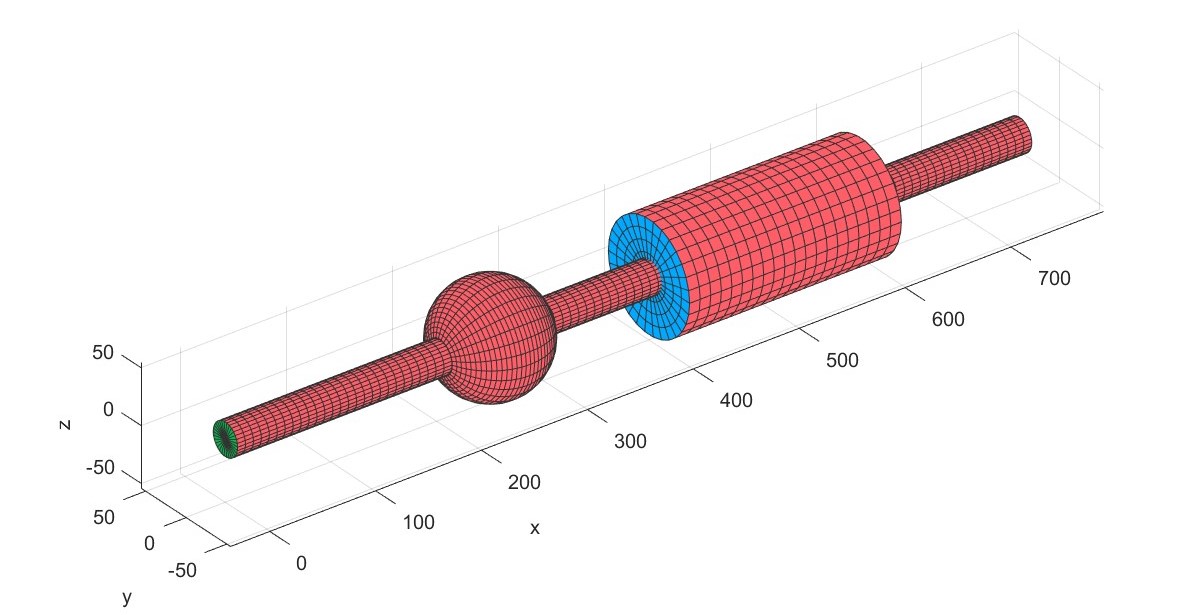
Add Blade (Flag=4)
OD=425;
inputshaft1.Length =1000;
inputshaft1.ID = [0,0];
inputshaft1.OD = [OD,OD];
paramsshaft1.Beam_N = 30;
obj1 = shaft.Commonshaft(paramsshaft1, inputshaft1);
obj1 = obj1.solve();
mat{1,1}=obj1.params.Material;
inputRotDyn.Shaft=obj1.output.BeamMesh;
inputRotDyn.Speed=[0,1500,3000];% Unit: RPM
inputRotDyn.MaterialNum=1;
inputRotDyn.BCNode=[1,1,1,1,0,0,0;size(obj1.output.Node,1),1,1,1,0,0,0];
paramsRotDyn.Material=mat;
paramsRotDyn.NMode=15;
paramsRotDyn.Freq=[0,3000];
paramsRotDyn.PrintCampbell=1;
paramsRotDyn.PrintMode=1;
paramsRotDyn.Position=[0,0,0,0,0,0];
Dyn = solve.RotDyn(paramsRotDyn,inputRotDyn);
[Dyn,Num1]= AddCnode(Dyn,500);
a=Point2D('Circle center');
a=AddPoint(a,[-160;-160;-155;-155;-95;-55;55;90;155;155;160;160;-160],...
[212.5;350;350;380;390;595;595;385;355;320;320;212.5;212.5]);
a=AddPoint(a,[-45;-20;18;45],...
[595;1050;1050;595]);
b1=Line2D('Section1');
b1=AddCurve(b1,a,1);
S1=Surface2D(b1);
b2=Line2D('Section2');
b2=AddCurve(b2,a,2);
S2=Surface2D(b2);
Dyn= AddUserdefinedDisc(Dyn,Num1,S1,1);
Dyn= AddBlade(Dyn,Num1,S2,1,30,3);
Plot(Dyn);
Dyn = Dyn.solve();
ANSYSSolve(Dyn.output.Assembly);
PlotCampbell(Dyn,'NMode',8);
for i=1:8
PlotORB(Dyn,2,i,'scale',100)
end
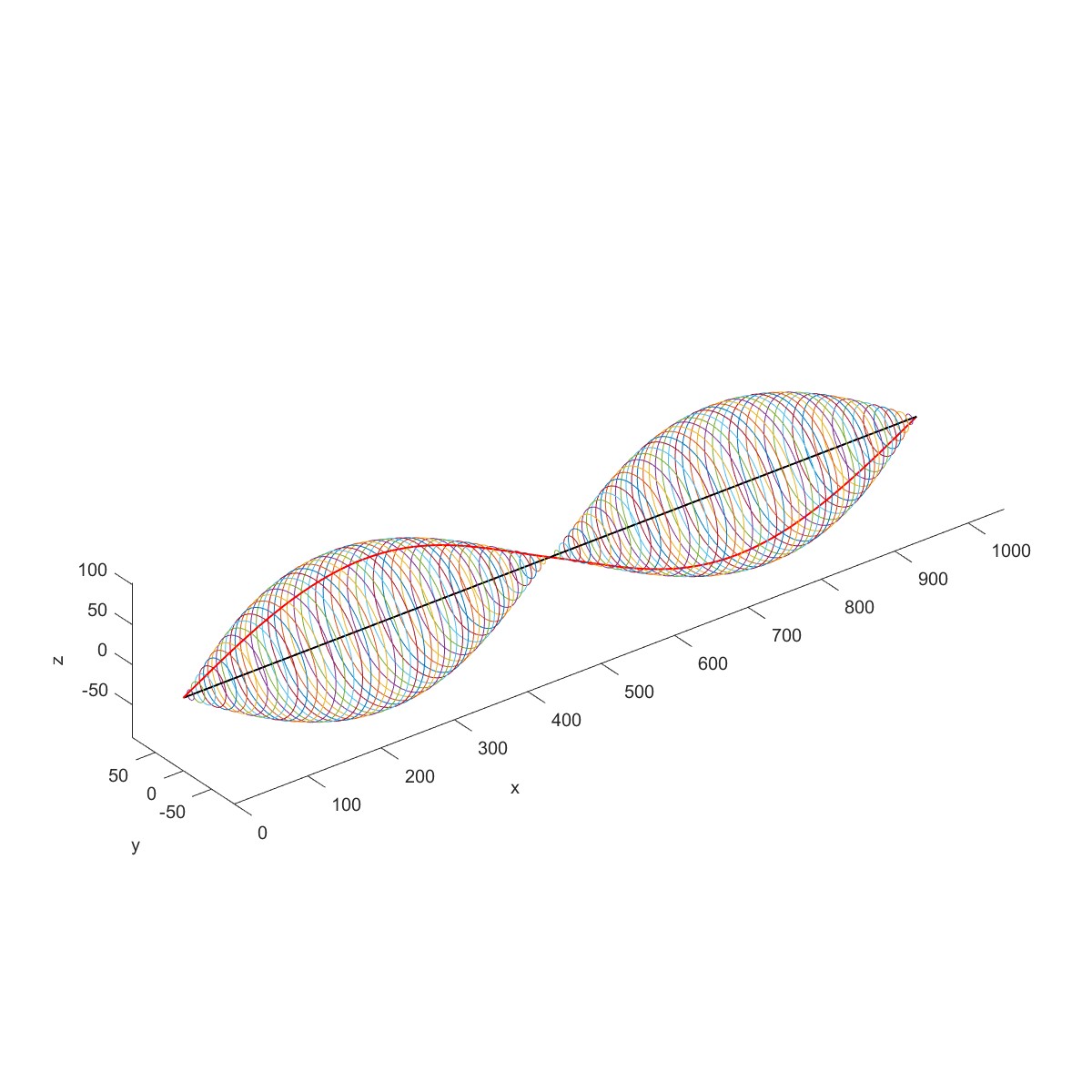
增加叶片,RotDyn会换算叶片的质量的转动惯量到轴中心。
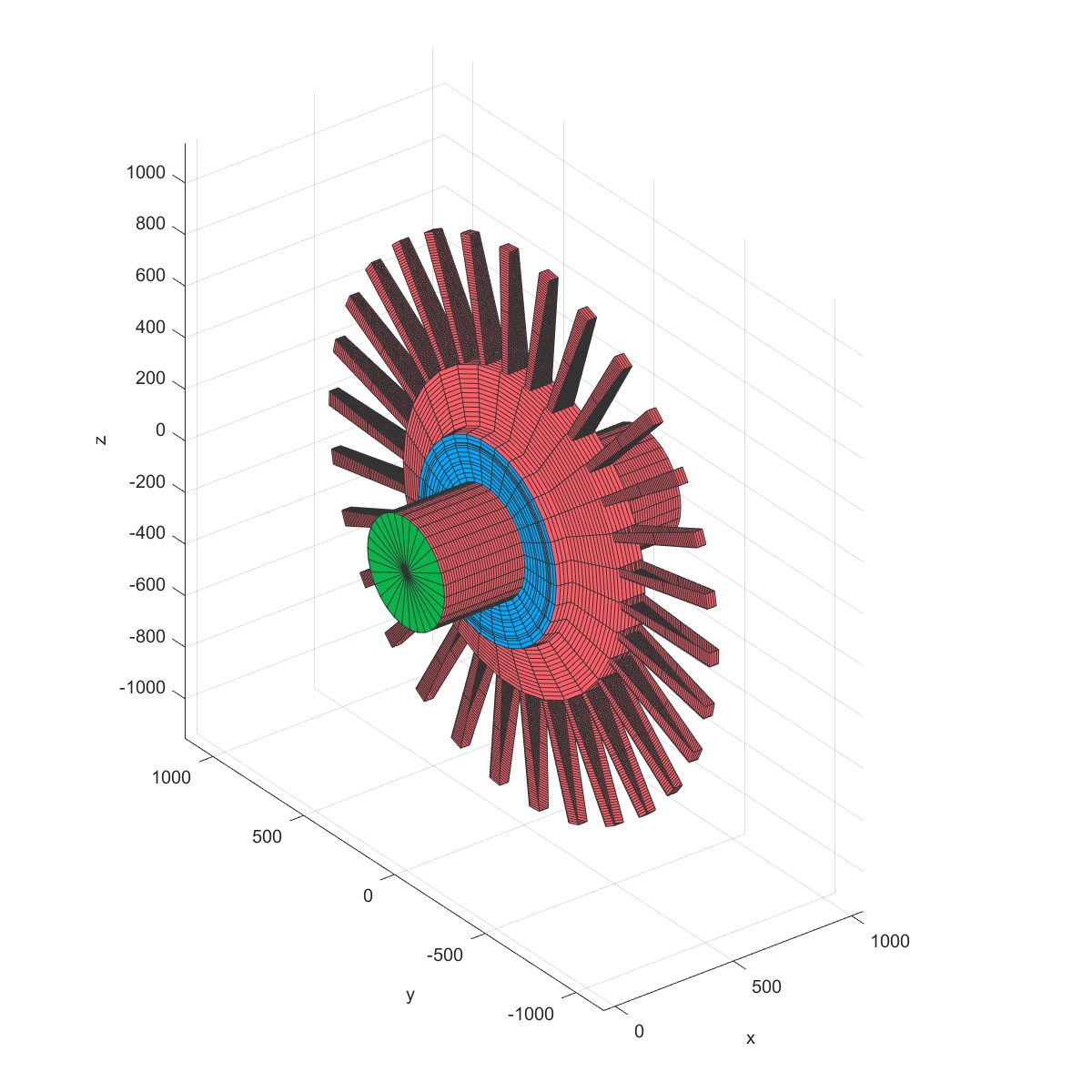 | 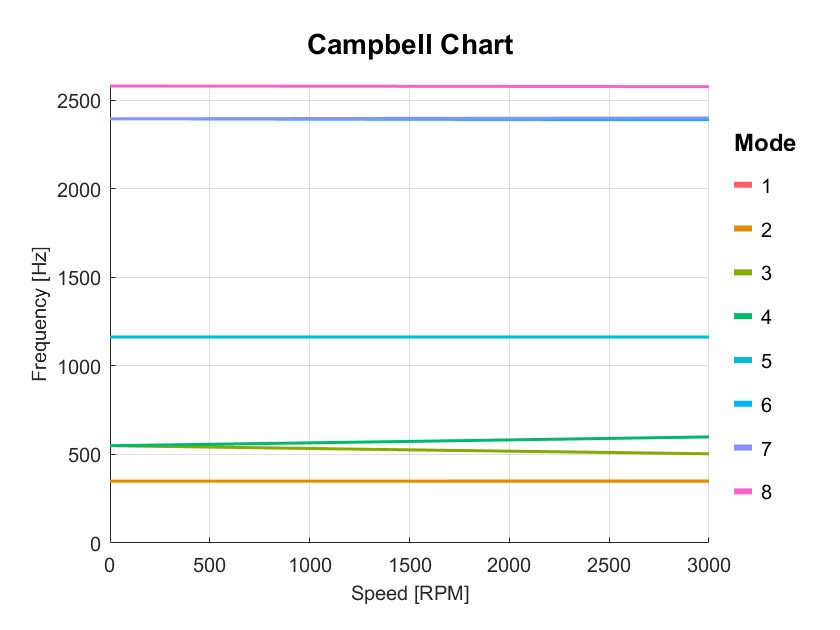 |
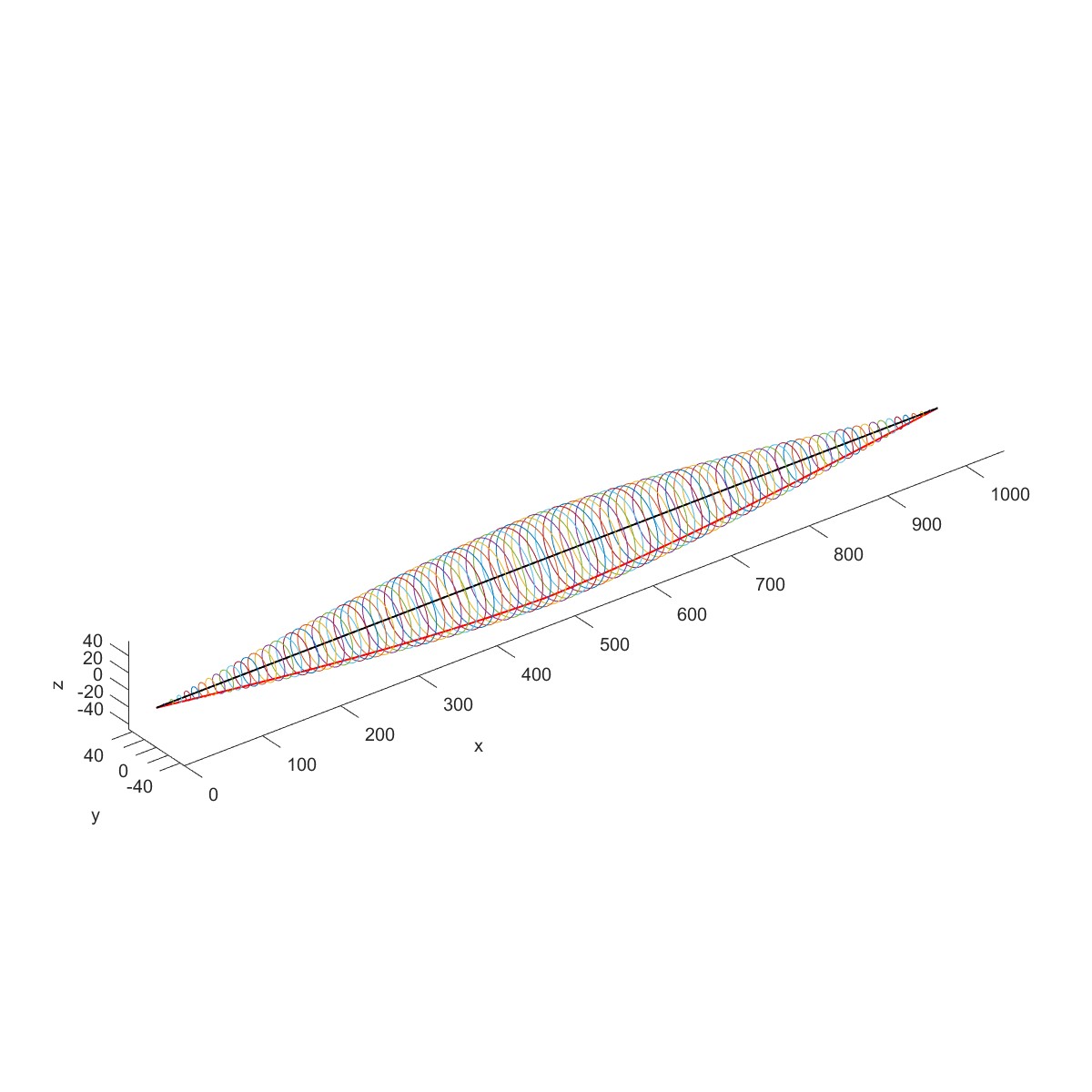 |  |
 |  |
 |  |
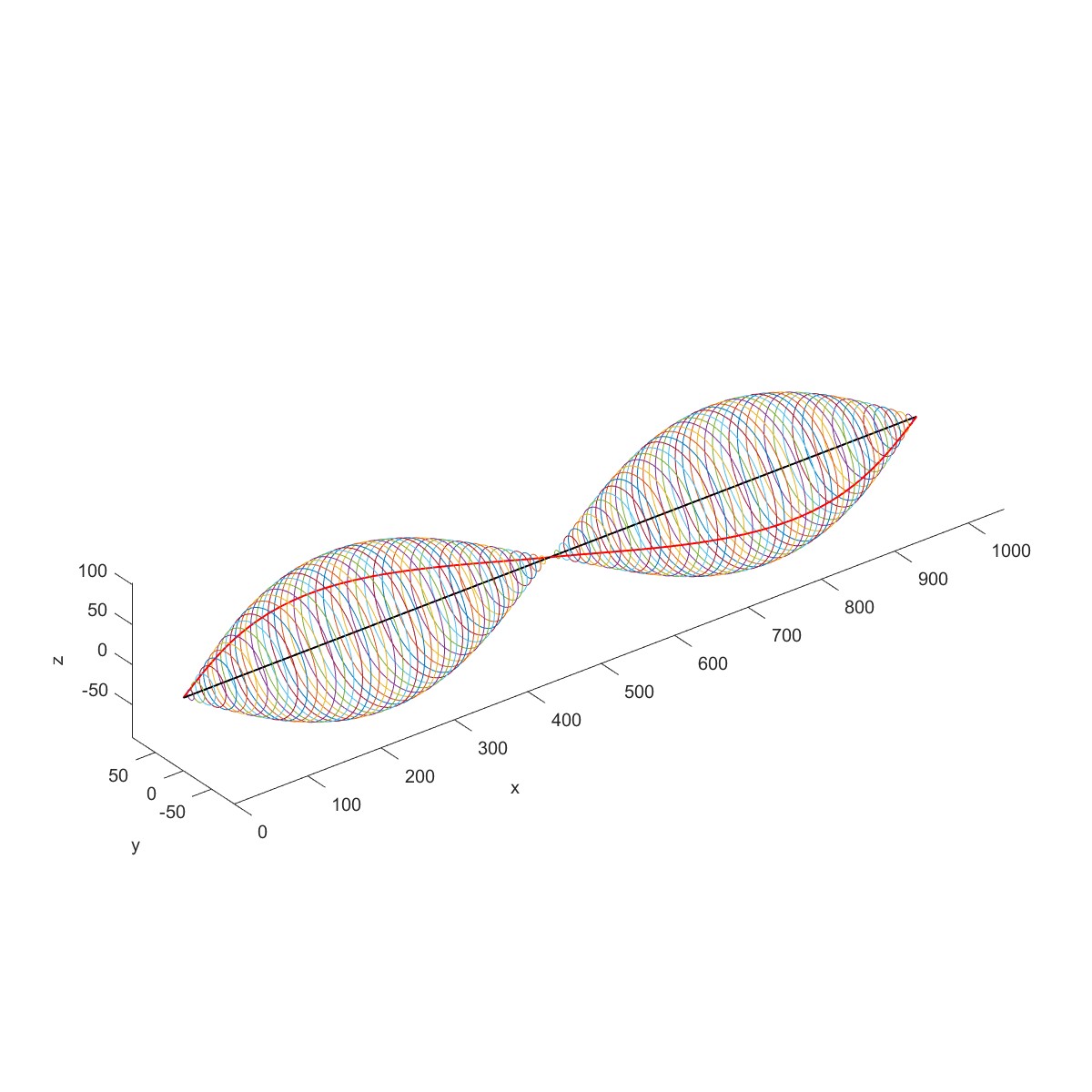 |  |
Multi Discs & Calculate critical speed (Flag=5)
m1=0.102;% unit:ton
JT1=6377*2;% unit: ton/mm2
JD1=6377;% unit: ton/mm2
% Shaft1
OD=50;% Unit: mm
inputshaft1.Length =1200;
inputshaft1.ID = [0,0];
inputshaft1.OD = [OD,OD];
paramsshaft1.Beam_N = 30;
obj1 = shaft.Commonshaft(paramsshaft1, inputshaft1);
obj1 = obj1.solve();
mat{1,1}=obj1.params.Material;
inputRotDyn.Shaft=obj1.output.BeamMesh;
inputRotDyn.Speed=[0,1000,2000,3000];% Unit: RPM
inputRotDyn.MaterialNum=1;
inputRotDyn.BCNode=[1,1,1,1,0,0,0];
paramsRotDyn.Material=mat;
paramsRotDyn.PrintCampbell=1;
Dyn = solve.RotDyn(paramsRotDyn,inputRotDyn);
[Dyn,Num1]= AddCnode(Dyn,400);
Dyn=AddPointMass(Dyn,Num1,m1,JT1,JD1);
[Dyn,Num2]= AddCnode(Dyn,800);
Bound=[1,1,1,0,0,0];
Dyn= AddBCNode(Dyn,Num2,Bound);
[Dyn,Num3]= AddCnode(Dyn,1200);
Dyn=AddPointMass(Dyn,Num3,m1,JT1,JD1);
Plot(Dyn);
Dyn = Dyn.solve();
ANSYSSolve(Dyn.output.Assembly);
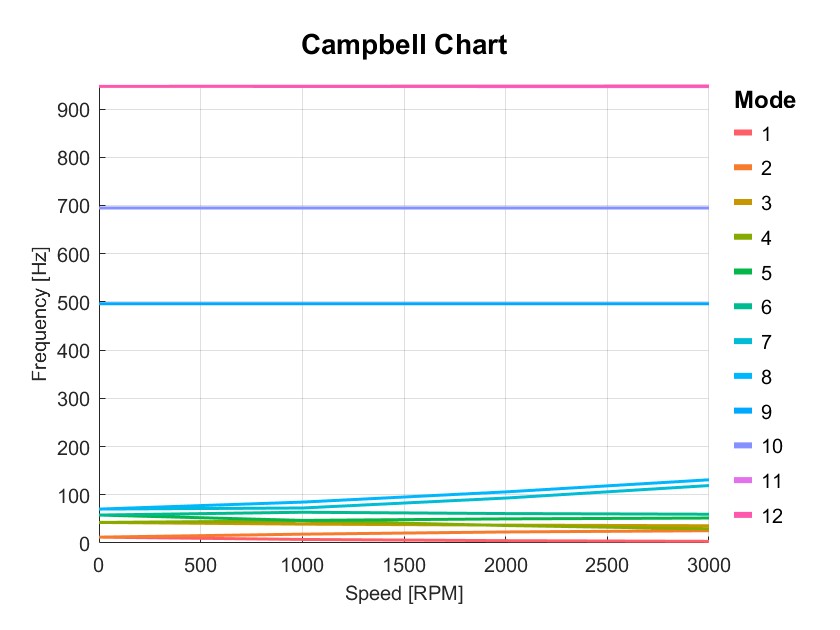
PlotCampbell(Dyn,'NMode',12);
Dyn=CalculateCriticalSpeed(Dyn);
disp(Dyn.output.CriticalSpeed);
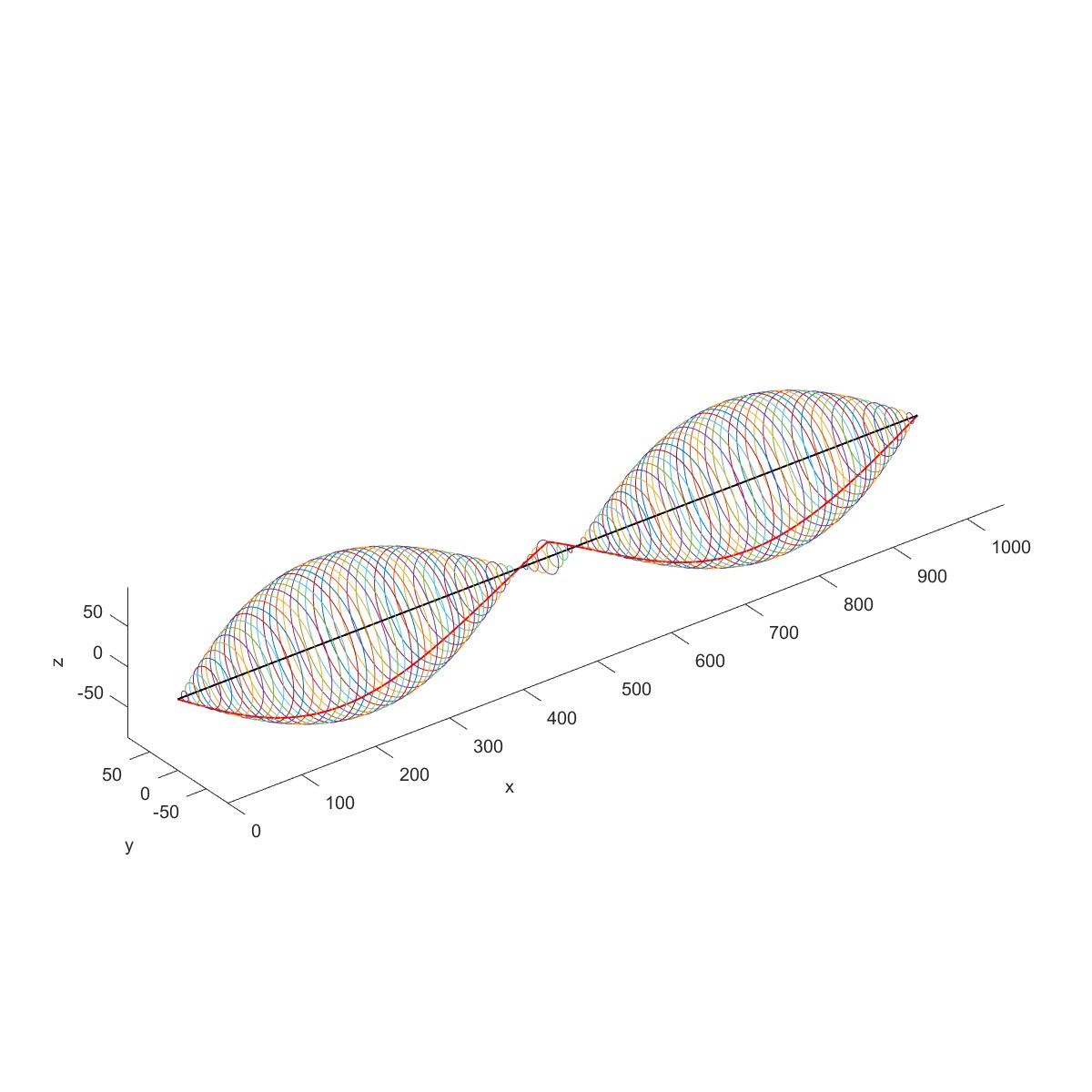
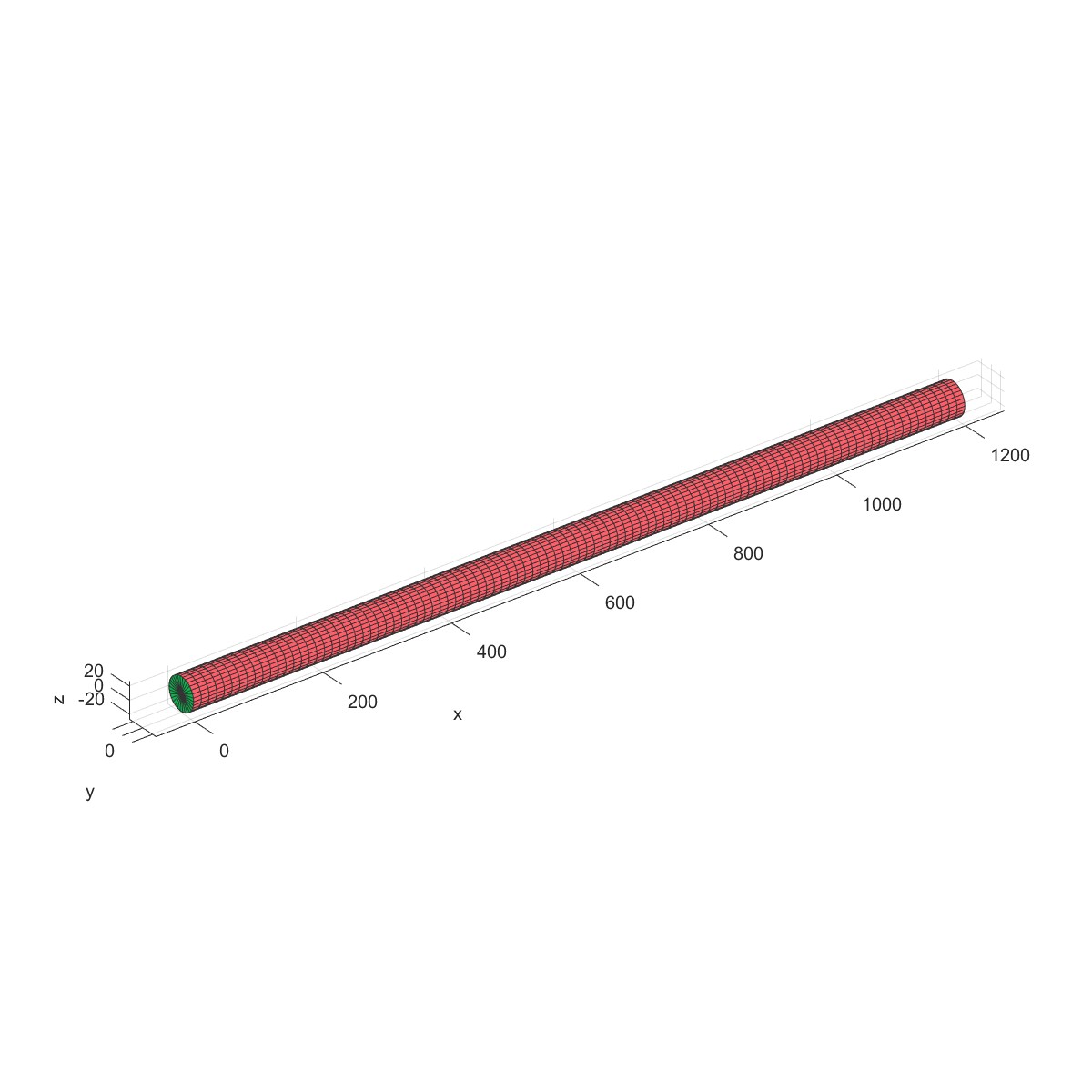
计算临界转速
 |  |
1.0e+03 *
0.5661
1.1379
2.2070
2.1237
Add Bearing (Flag=6)
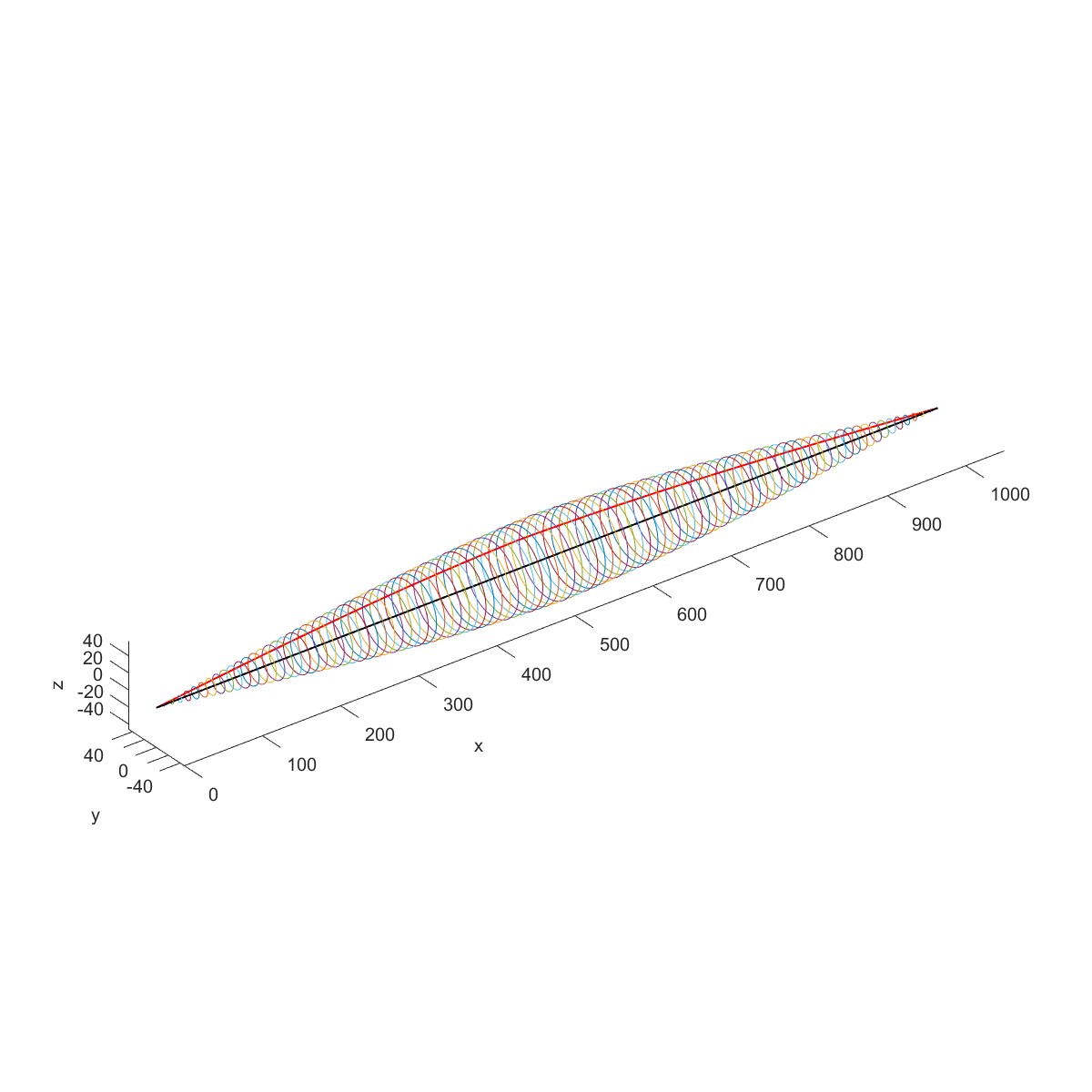
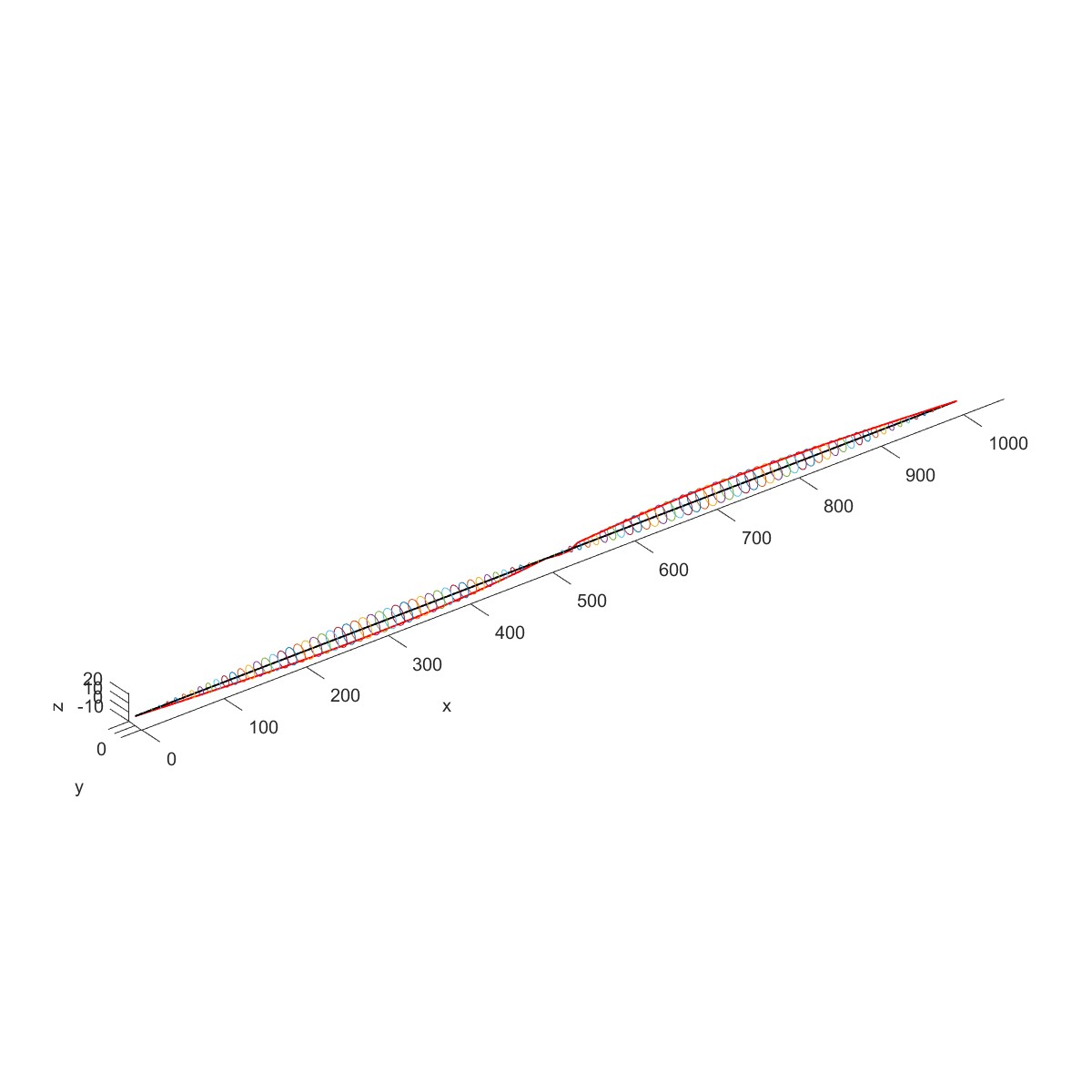
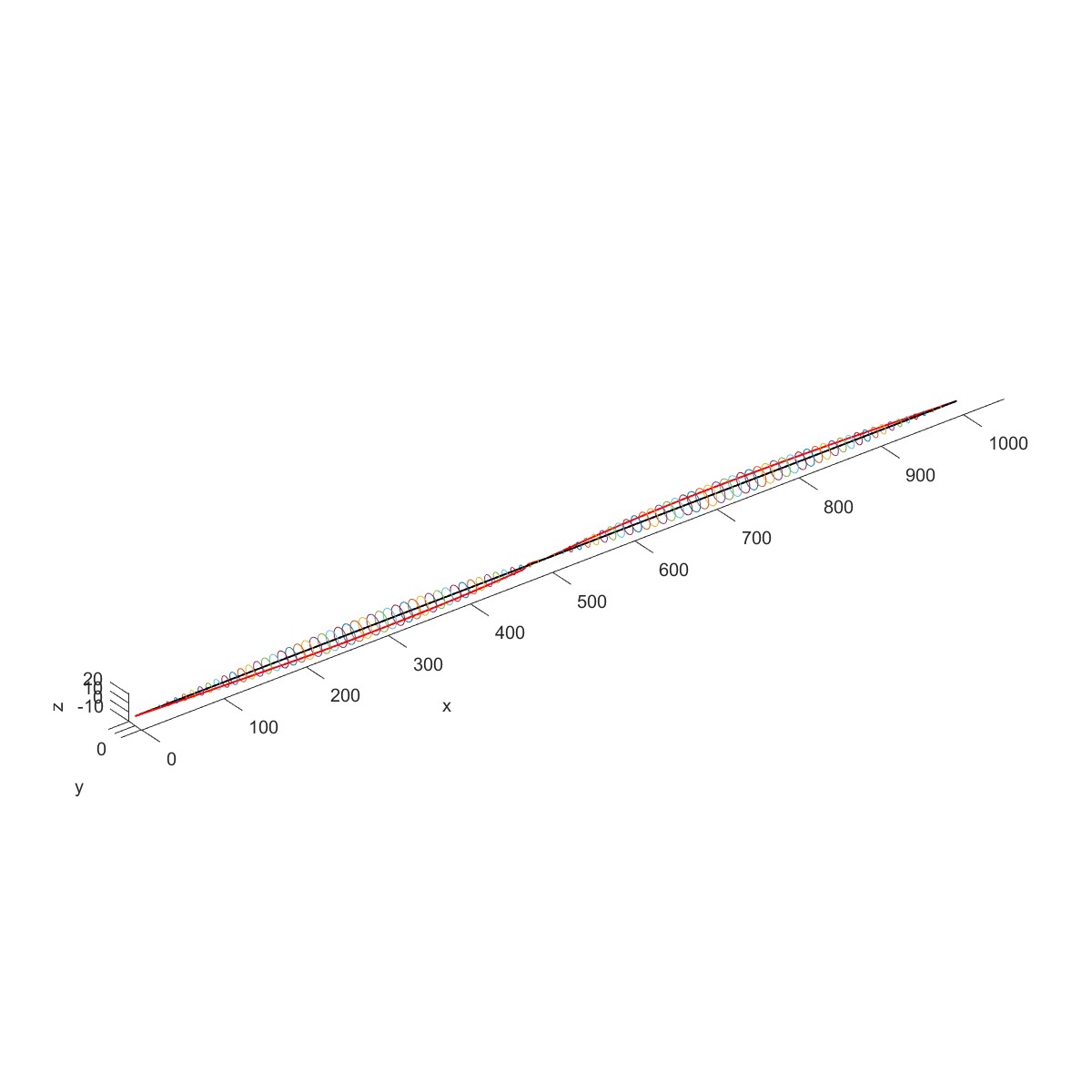
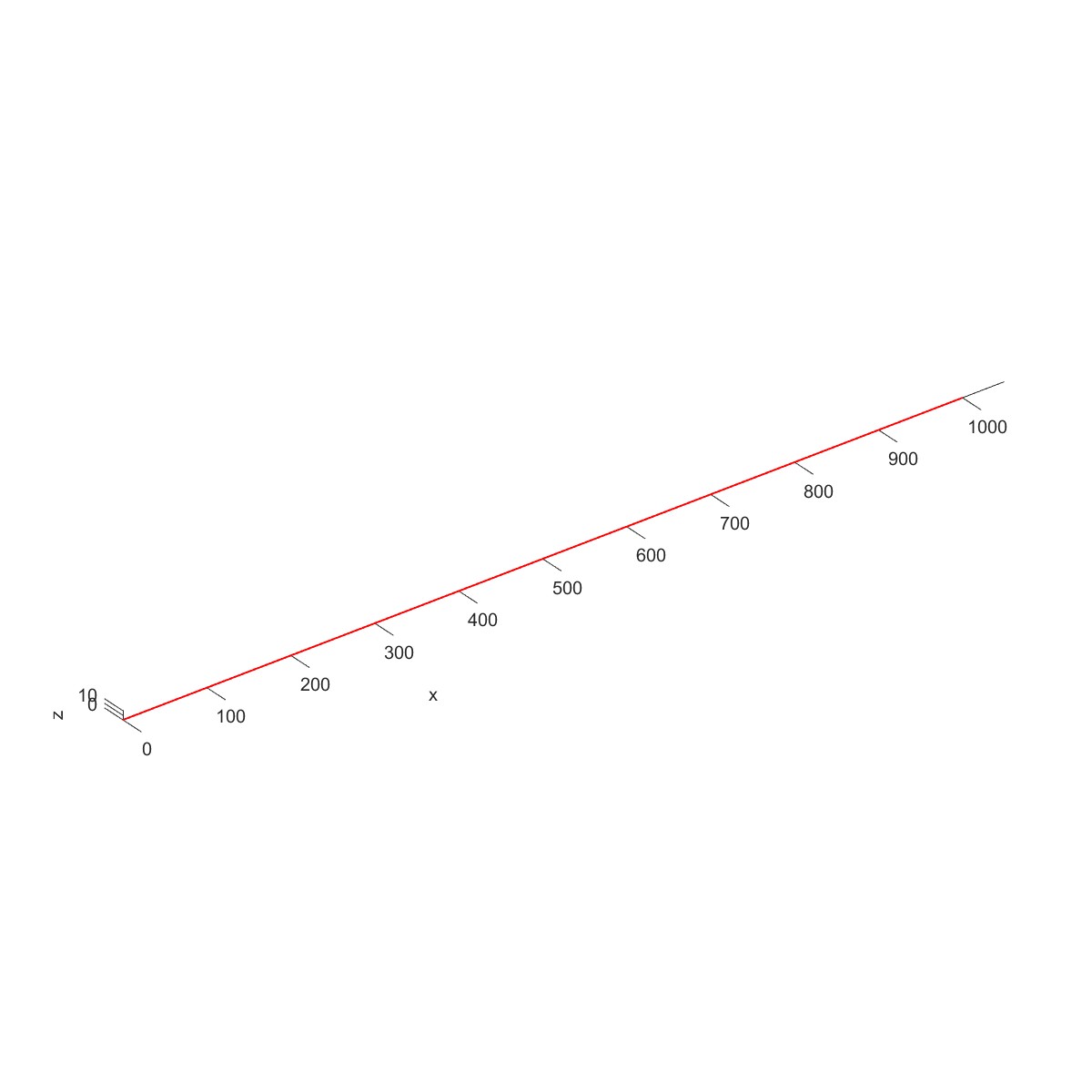
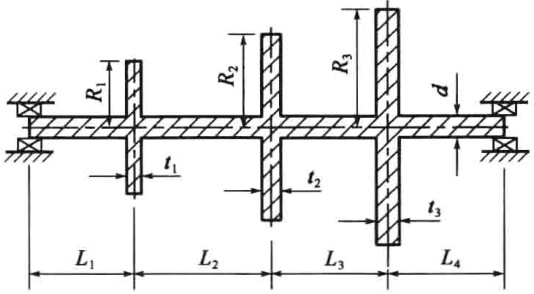
如下图所示钢质圆盘转子结构,材料的弹性模量为$200\mathrm{GPa}$,密度$7830kg/m^{3}$,泊松系数为0.3,长度分别为$L_1=0.2m$,$L_2=0 ~ 3m$,$L_3=0.5m$,$L_4=0.3m$,轴径$d=0.05m$,圆盘半径分别为 $R_{1}=0.12m$ , $R_{2}=0~2m$ , $R_{3}=0.2m$ ,厚度分别为 $t_{1}=0.05m$ , $t_{2}=0.05m$ , $t_{3}=0.06m$ 。轴两端为简支边界条件,图中支承仅为示意。
L1=200;
L2=300;
L3=500;
L4=300;
t1=50;t2=50;t3=60;
R1=120;
R2=200;
R3=200;
d=50;
% Shaft1
inputshaft1.Length = [L1-t1/2;L1+t1/2;L1+L2-t2/2;L1+L2+t2/2;L1+L2+L3-t3/2;L1+L2+L3+t3/2;L1+L2+L3+L4];
inputshaft1.ID = [[0,0];[0,0];[0,0];[0,0];[0,0];[0,0];[0,0]];
inputshaft1.OD = [[d,d];[R1*2,R1*2];[d,d];[R2*2,R2*2];[d,d];[R3*2,R3*2];[d,d]];
paramsshaft1.Beam_N = 16;
paramsshaft1.N_Slice=201;
obj1 = shaft.Commonshaft(paramsshaft1, inputshaft1);
obj1 = obj1.solve();
Plot3D(obj1)
% Rigid Boundary
mat{1,1}=obj1.params.Material;
inputRotDyn.Shaft=obj1.output.BeamMesh;
inputRotDyn.Speed=[0,1000,2000,3000,4000,5000,6000];
inputRotDyn.MaterialNum=1;
inputRotDyn.BCNode=[1,1,1,1,1,0,0;size(obj1.output.Node,1),0,1,1,1,0,0];
paramsRotDyn.Material=mat;
paramsRotDyn.PrintCampbell=1;
paramsRotDyn.ShaftTorsion=1;
paramsRotDyn.PrintMode=1;
Dyn1 = solve.RotDyn(paramsRotDyn,inputRotDyn);
Dyn1 = Dyn1.solve();
Plot(Dyn1);
ANSYSSolve(Dyn1.output.Assembly);
Dyn1=PlotCampbell(Dyn1,'NMode',12);
% Bearing
mat{1,1}=obj1.params.Material;
inputRotDyn.Shaft=obj1.output.BeamMesh;
inputRotDyn.Speed=[0,1000,2000,3000,4000,5000,6000];
inputRotDyn.MaterialNum=1;
inputRotDyn.Bearing=[1,1e8,8e3,3e3,0,0,0,1e-3*8e3,2e-4*3e3,0,0;size(obj1.output.Node,1),0,8e3,3e3,0,0,0,1e-3*8e3,2e-4*3e3,0,0];
paramsRotDyn.Material=mat;
paramsRotDyn.PrintCampbell=1;
paramsRotDyn.ShaftTorsion=1;
paramsRotDyn.PrintMode=1;
inputRotDyn.BCNode=[];
Dyn2 = solve.RotDyn(paramsRotDyn,inputRotDyn);
Dyn2 = Dyn2.solve();
Plot(Dyn2);
ANSYSSolve(Dyn2.output.Assembly);
Dyn2=PlotCampbell(Dyn2,'NMode',12);
disp(Dyn1.output.Campbell);
disp(Dyn2.output.Campbell);
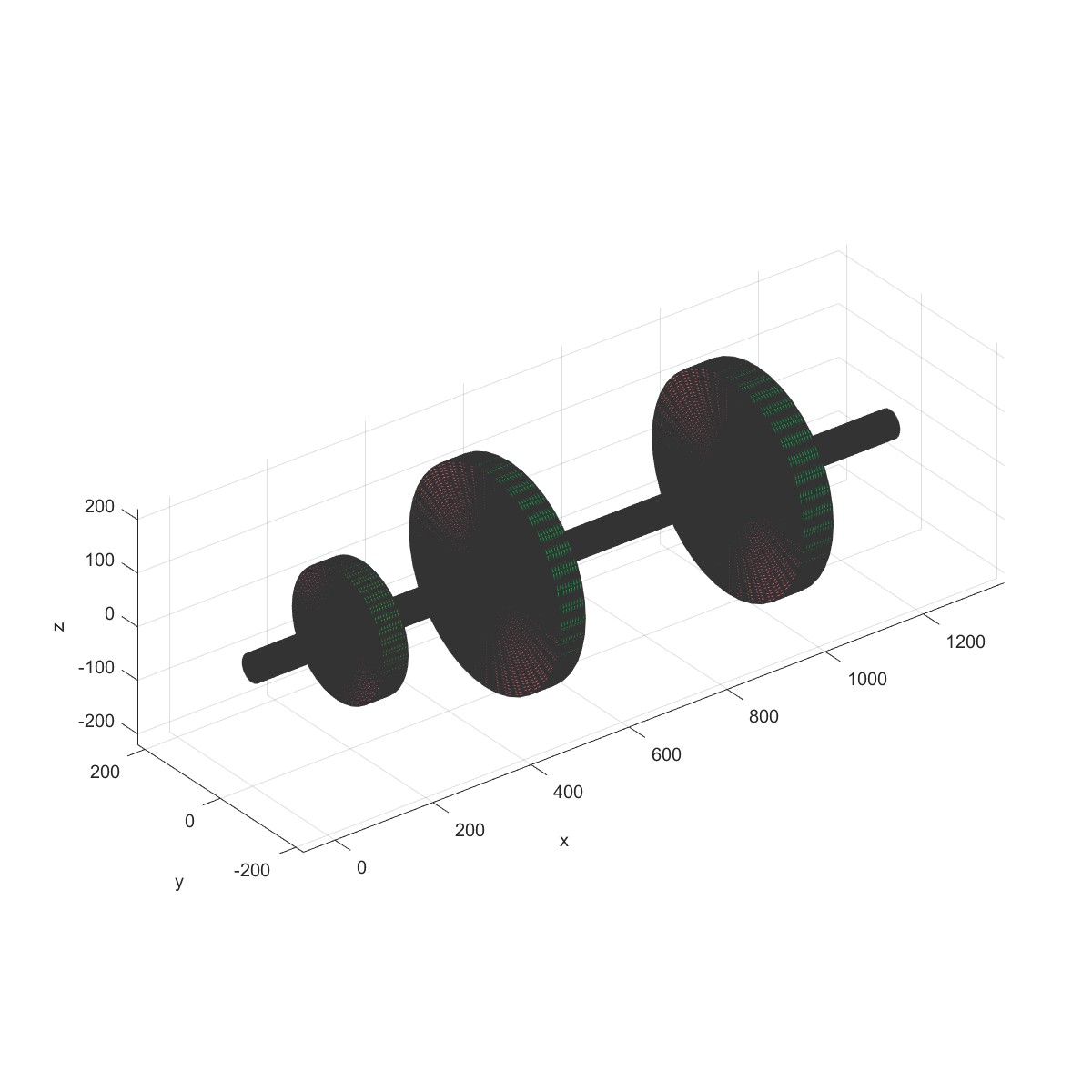 | 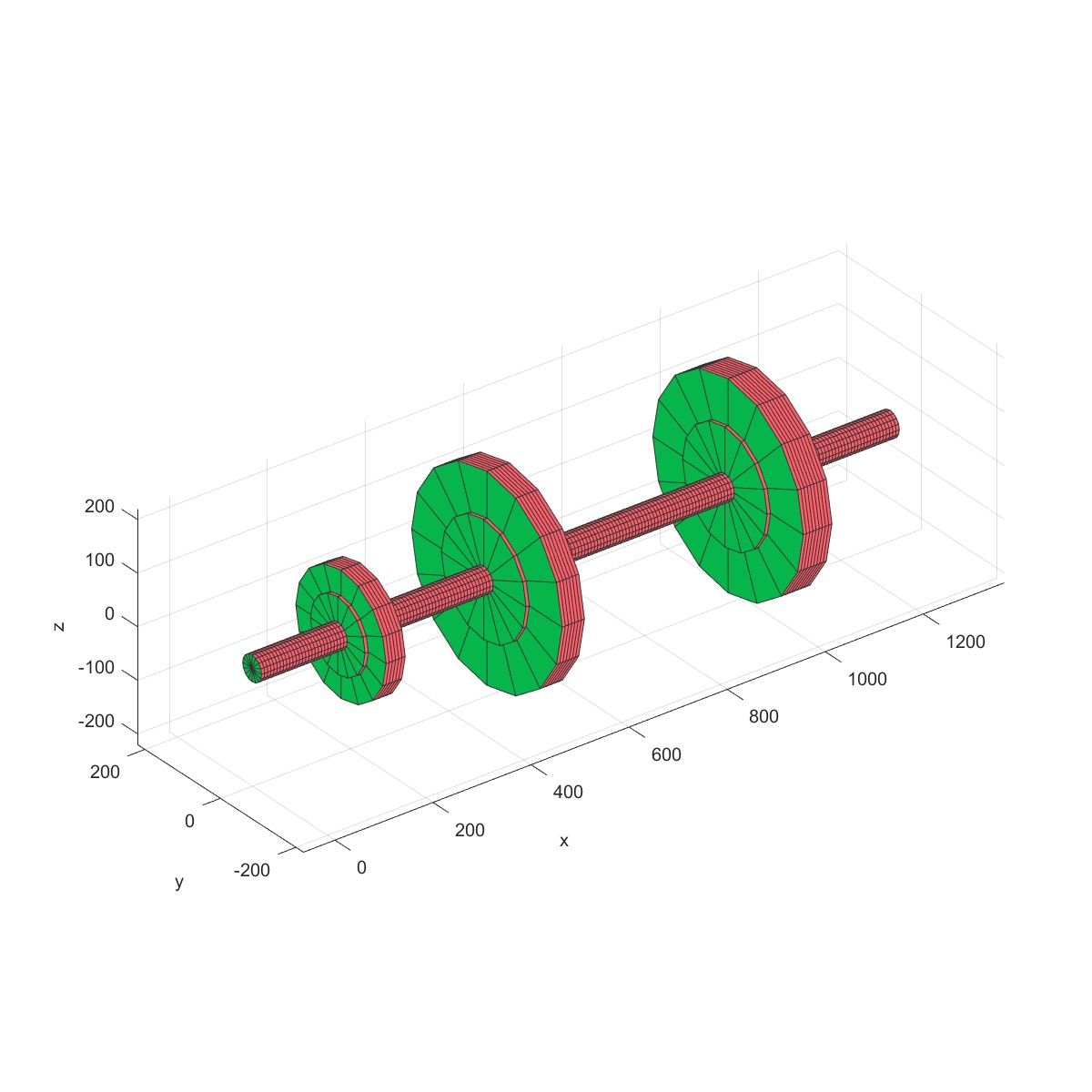 |
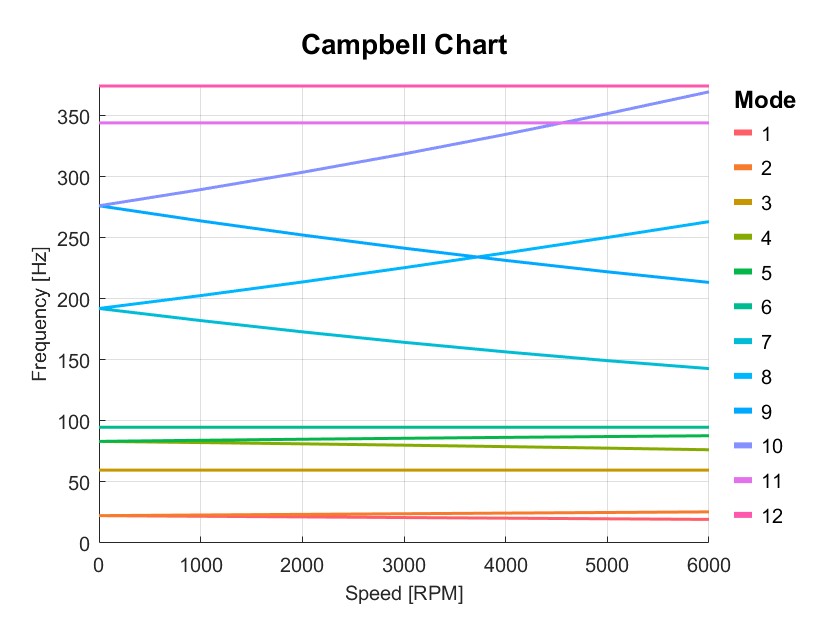 |  |
Num Status rpm1 rpm2 rpm3 rpm4 rpm5 rpm6 rpm7
1 BW 22.406 21.884 21.362 20.842 20.325 19.813 19.306
2 FW 22.406 22.927 23.447 23.963 24.476 24.983 25.484
3
4 BW 83.198 82.229 81.192 80.086 78.909 77.662 76.348
5 FW 83.198 84.104 84.95 85.739 86.477 87.167 87.812
6
7 BW 192.02 182.11 172.88 164.33 156.47 149.3 142.8
8 FW 192.02 202.57 213.71 225.39 237.56 250.16 263.13
9 BW 276.11 263.73 252.17 241.41 231.38 222.05 213.37
10 FW 276.11 289.36 303.5 318.57 334.58 351.53 369.4
11
12
Num Status rpm1 rpm2 rpm3 rpm4 rpm5 rpm6 rpm7
1
2 BW 18.664 18.619 18.493 18.303 18.068 17.8 17.509
3 FW 20.791 20.826 20.923 21.064 21.232 21.415 21.604
4 BW 52.486 52.442 52.309 52.091 51.792 51.417 50.975
5 FW 67.5 67.53 67.619 67.765 67.962 68.203 68.474
6
7 BW 111.47 110.32 107.02 102.22 96.835 91.461 86.372
8 FW 139.56 140.57 143.51 147.72 151.88 153.96 154.25
9 FW 189.93 189.95 188.82 183.53 177.41 174.04 172.86
10 FW 209.4 210.66 215.61 227.17 242.31 258.84 276.84
11
12 BW 291.24 291.46 292.14 293.25 294.77 296.63 298.55
Add LUT Bearing (Flag=7)
当轴承刚度随转速变化时,可以采用LUTBearing (Look up table bearing)模拟。
L1=200;
L2=300;
L3=500;
L4=300;
t1=50;t2=50;t3=60;
R1=120;
R2=200;
R3=200;
d=50;
% Shaft1
inputshaft1.Length = [L1-t1/2;L1+t1/2;L1+L2-t2/2;L1+L2+t2/2;L1+L2+L3-t3/2;L1+L2+L3+t3/2;L1+L2+L3+L4];
inputshaft1.ID = [[0,0];[0,0];[0,0];[0,0];[0,0];[0,0];[0,0]];
inputshaft1.OD = [[d,d];[R1*2,R1*2];[d,d];[R2*2,R2*2];[d,d];[R3*2,R3*2];[d,d]];
paramsshaft1.Beam_N = 16;
paramsshaft1.N_Slice=201;
obj1 = shaft.Commonshaft(paramsshaft1, inputshaft1);
obj1 = obj1.solve();
Plot3D(obj1)
% LUTBearing
RPM=[0,2000,4000,6000,8000,10000,12000]';
K11=[1.6e3,2e3,4.8e3,8.8e3,1.3e4,1.8e4,2.3e4]';
K22=[2e3,3e3,6e3,1.1e4,1.7e4,2.3e4,3e4]';
K12=[-2e1,-2.4e1,-6.8e1,-1.2e2,-1.9e2,-2.6e2,-3.6e2]';
K21=[6,4e1,1e2,1.7e2,2.5e2,3.4e2,4.3e2]';
C11=[2,2,2,2,2,2,2]';
C22=[5,5,5,5,5,5,5]';
C12=[-4,-4,-4,-4,-4,-4,-4]';
C21=[3,3,3,3,3,3,3]';
LUTBearing=table(RPM,K11,K22,K12,K21,C11,C22,C12,C21);
mat{1,1}=obj1.params.Material;
inputRotDyn.Shaft=obj1.output.BeamMesh;
inputRotDyn.Speed=[0,1000,2000,3000,4000,5000,6000];
inputRotDyn.MaterialNum=1;
inputRotDyn.Bearing=[1,1e8,0,0,0,0,0,0,0,0,0];
paramsRotDyn.Material=mat;
paramsRotDyn.PrintCampbell=1;
paramsRotDyn.ShaftTorsion=1;
paramsRotDyn.PrintMode=1;
inputRotDyn.BCNode=[];
Dyn2 = solve.RotDyn(paramsRotDyn,inputRotDyn);
Dyn2=AddTable(Dyn2,LUTBearing);
Dyn2=AddLUTBearing(Dyn2,1,1);% Node 1, Table 1
Dyn2=AddLUTBearing(Dyn2,size(obj1.output.Node,1),1);
Dyn2 = Dyn2.solve();
Plot(Dyn2);
ANSYSSolve(Dyn2.output.Assembly);
Dyn2=PlotCampbell(Dyn2,'NMode',12);
disp(Dyn2.output.Campbell);
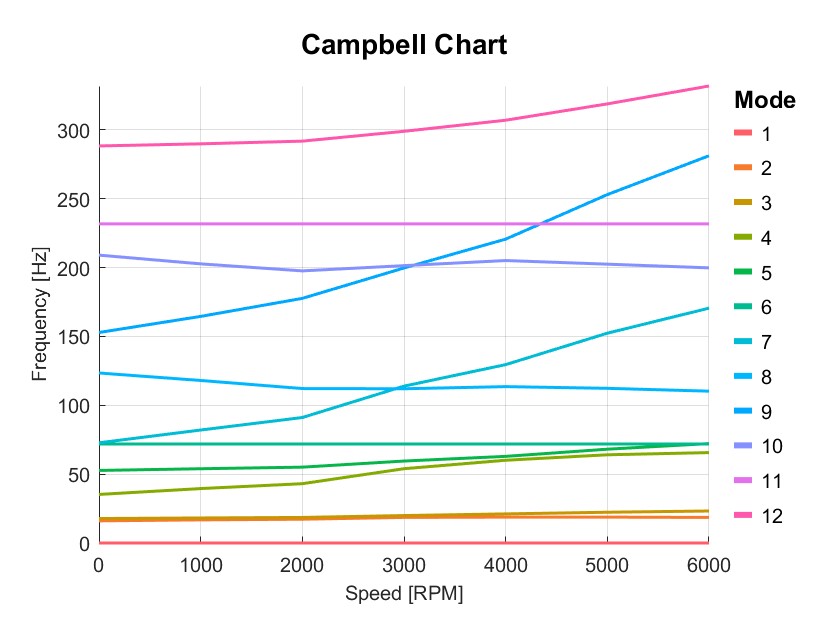
Num Status rpm1 rpm2 rpm3 rpm4 rpm5 rpm6 rpm7
1
2 BW 16.089 16.794 17.278 18.588 18.787 18.79 18.578
3 FW 17.774 18.189 18.562 19.94 21.134 22.342 23.243
4 BW 35.277 39.528 43.083 53.953 60.107 64.07 65.661
5 FW 52.696 53.937 55.088 59.522 62.923 68.139 72.199
6
7 FW 72.781 82.061 91.141 113.93 129.56 152.39 170.57
8 BW 123.47 118.04 112.17 112.02 113.58 112.34 110.29
9 FW 152.9 164.59 177.68 199.74 220.7 253.04 281.26
10 BW 209.09 202.74 197.64 201.45 205.16 202.52 199.84
11
12 BW 288.39 289.92 291.88 299.02 307.07 318.93 331.93
Consider prestress (Flag=8)
L1=200;
L2=300;
L3=500;
L4=300;
t1=50;t2=50;t3=60;
R1=120;
R2=200;
R3=200;
d=50;
% Shaft1
inputshaft1.Length = [L1-t1/2;L1+t1/2;L1+L2-t2/2;L1+L2+t2/2;L1+L2+L3-t3/2;L1+L2+L3+t3/2;L1+L2+L3+L4];
inputshaft1.ID = [[0,0];[0,0];[0,0];[0,0];[0,0];[0,0];[0,0]];
inputshaft1.OD = [[d,d];[R1*2,R1*2];[d,d];[R2*2,R2*2];[d,d];[R3*2,R3*2];[d,d]];
paramsshaft1.Beam_N = 16;
paramsshaft1.N_Slice=201;
obj1 = shaft.Commonshaft(paramsshaft1, inputshaft1);
obj1 = obj1.solve();
Plot3D(obj1)
% Elastic support
mat{1,1}=obj1.params.Material;
inputRotDyn.Shaft=obj1.output.BeamMesh;
inputRotDyn.Speed=[0,1000,2000,3000,4000,5000,6000];
inputRotDyn.MaterialNum=1;
inputRotDyn.Support=[1,1e8,8e3,3e3,0,0,0,1e-3,2e-4,0,0;size(obj1.output.Node,1),0,8e3,3e3,0,0,0,1e-3,2e-4,0,0];
paramsRotDyn.Material=mat;
paramsRotDyn.PrintCampbell=1;
paramsRotDyn.ShaftTorsion=1;
paramsRotDyn.Material=mat;
paramsRotDyn.PStress=1;
Dyn2 = solve.RotDyn(paramsRotDyn,inputRotDyn);
Dyn2 = Dyn2.solve();
Plot(Dyn2);
ANSYSSolve(Dyn2.output.Assembly);
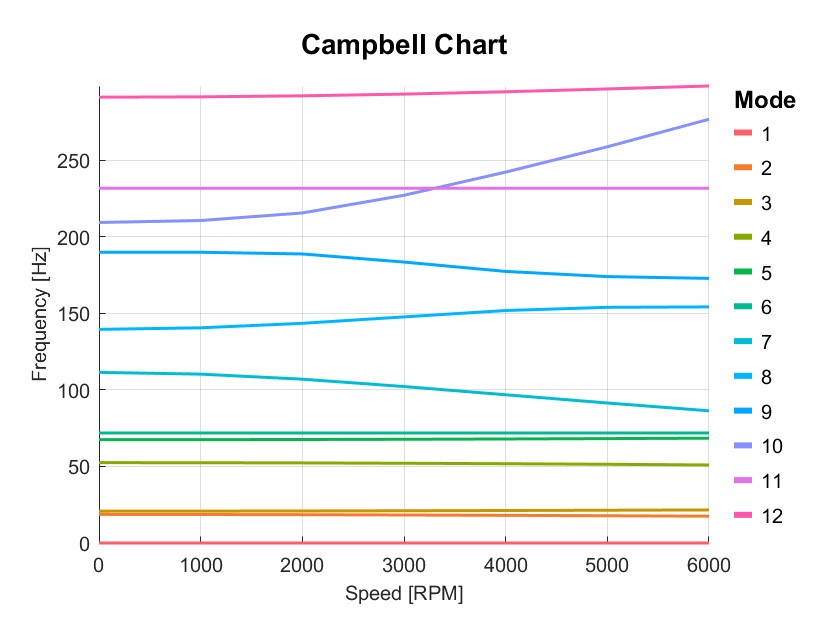
Dyn2=PlotCampbell(Dyn2,'NMode',12);
disp(Dyn2.output.Campbell);
Num Status rpm1 rpm2 rpm3 rpm4 rpm5 rpm6 rpm7
1
2 BW 18.664 18.619 18.493 18.303 18.068 17.8 17.509
3 FW 20.791 20.826 20.923 21.064 21.232 21.415 21.604
4 BW 52.486 52.442 52.309 52.091 51.792 51.417 50.975
5 FW 67.5 67.53 67.619 67.765 67.962 68.203 68.474
6
7 BW 111.47 110.32 107.02 102.22 96.835 91.461 86.372
8 FW 139.56 140.57 143.51 147.72 151.88 153.96 154.25
9 FW 189.93 189.95 188.82 183.53 177.41 174.04 172.86
10 FW 209.4 210.66 215.61 227.17 242.31 258.84 276.84
11
12 BW 291.24 291.46 292.14 293.25 294.77 296.63 298.55
Eccentricity of shaft (Flag=9)
考虑轴偏心对模拟影响,设置ex和ey(轴两端偏心量)对模拟的影响。
L1=200;
L2=300;
L3=500;
L4=300;
t1=50;t2=50;t3=60;
R1=120;
R2=200;
R3=200;
d=50;
% Shaft1
inputshaft1.Length = [L1-t1/2;L1+t1/2;L1+L2-t2/2;L1+L2+t2/2;L1+L2+L3-t3/2;L1+L2+L3+t3/2;L1+L2+L3+L4];
inputshaft1.ID = [[0,0];[0,0];[0,0];[0,0];[0,0];[0,0];[0,0]];
inputshaft1.OD = [[d,d];[R1*2,R1*2];[d,d];[R2*2,R2*2];[d,d];[R3*2,R3*2];[d,d]];
paramsshaft1.Beam_N = 16;
paramsshaft1.N_Slice=201;
obj1 = shaft.Commonshaft(paramsshaft1, inputshaft1);
obj1 = obj1.solve();
% Rigid Boundary
mat{1,1}=obj1.params.Material;
inputRotDyn.Shaft=obj1.output.BeamMesh;
inputRotDyn.Speed=[0,1000,2000,3000,4000,5000,6000];
inputRotDyn.MaterialNum=1;
inputRotDyn.BCNode=[1,1,1,1,1,0,0;size(obj1.output.Node,1),0,1,1,1,0,0];
paramsRotDyn.Material=mat;
paramsRotDyn.PrintCampbell=1;
paramsRotDyn.ShaftTorsion=1;
paramsRotDyn.PrintMode=1;
paramsRotDyn.ey=[5,-5];
Dyn1 = solve.RotDyn(paramsRotDyn,inputRotDyn);
Dyn1 = Dyn1.solve();
Plot(Dyn1);
ANSYSSolve(Dyn1.output.Assembly);
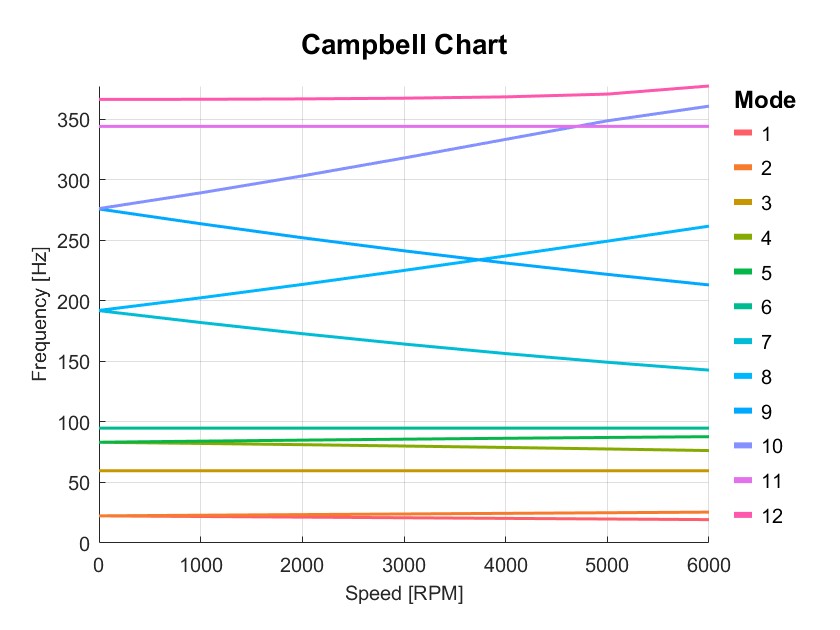
Dyn1=PlotCampbell(Dyn1,'NMode',12);
disp(Dyn1.output.Campbell);
Num Status rpm1 rpm2 rpm3 rpm4 rpm5 rpm6 rpm7
1 BW 22.405 21.883 21.362 20.842 20.325 19.812 19.305
2 FW 22.406 22.927 23.446 23.963 24.475 24.982 25.483
3 BW 59.647 59.647 59.647 59.647 59.647 59.647 59.647
4 BW 83.165 82.211 81.173 80.064 78.884 77.632 76.311
5 FW 83.198 84.087 84.931 85.719 86.455 87.142 87.785
6 BW 94.803 94.803 94.803 94.803 94.803 94.803 94.803
7 BW 191.83 182.03 172.8 164.26 156.4 149.23 142.72
8 FW 192.02 202.43 213.49 225.03 236.96 249.19 261.6
9 BW 275.76 263.58 252.03 241.24 231.17 221.79 213.07
10 FW 276.1 289.1 303.09 317.86 333.25 348.56 360.66
11 FW 343.94 343.94 343.94 343.94 343.94 343.93 343.94
12 FW 366.24 366.34 366.65 367.25 368.33 370.62 377.31
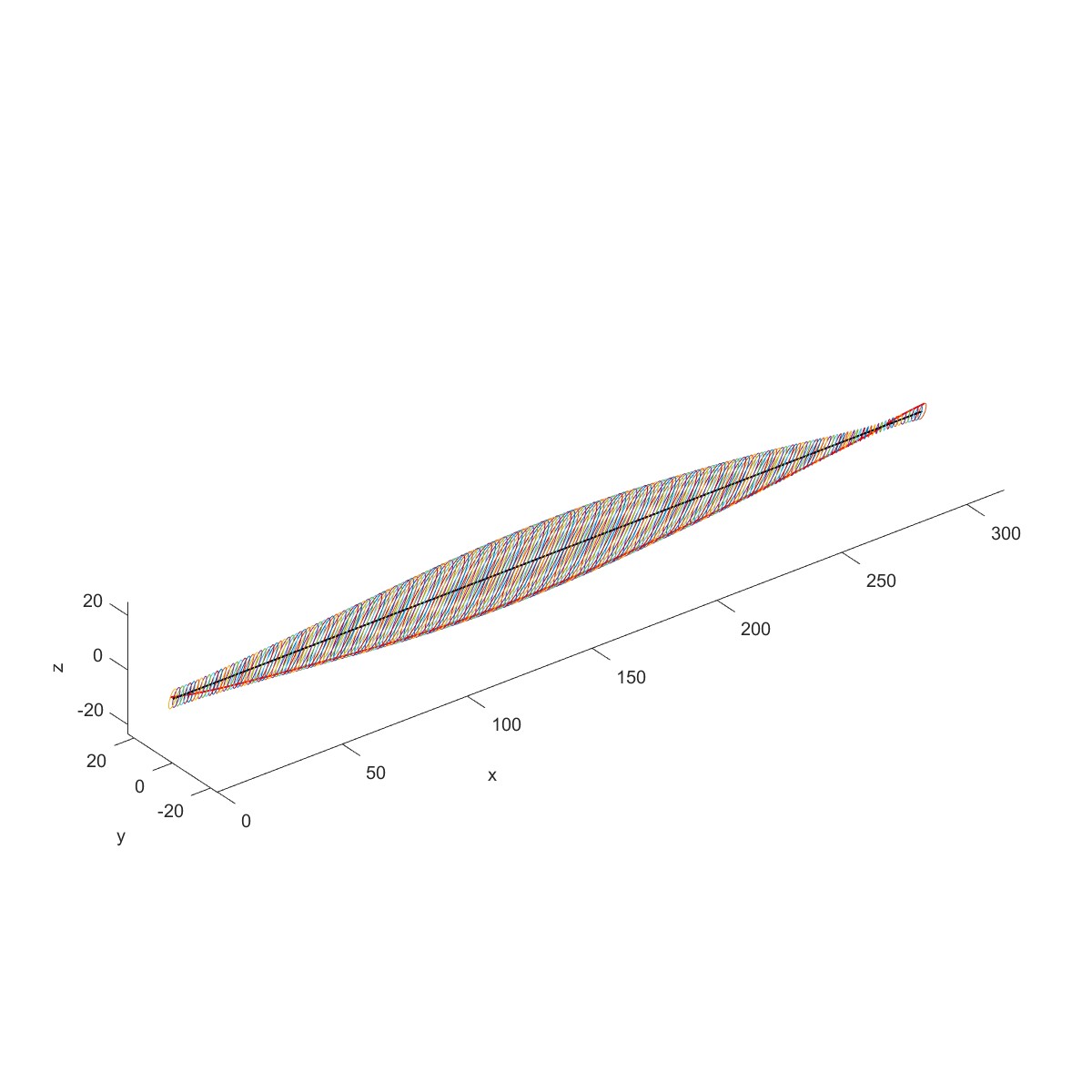
High speed rotor example (Flag=10)
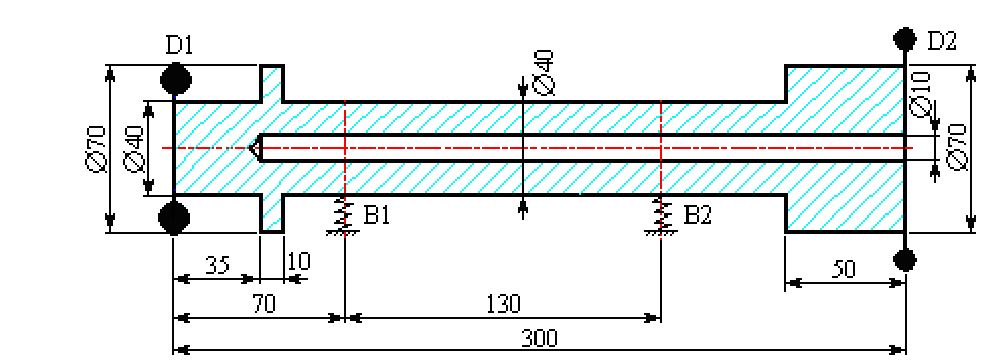
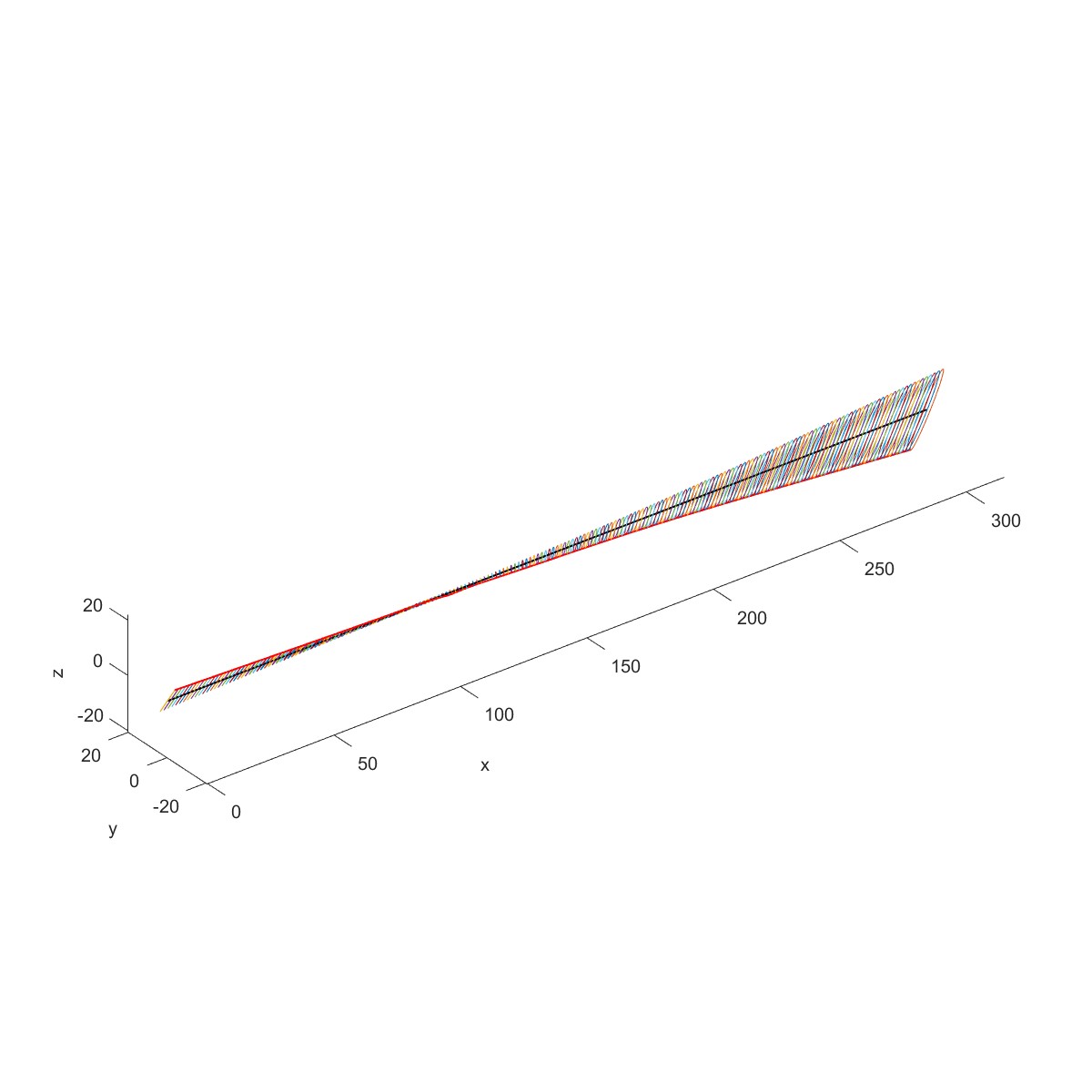
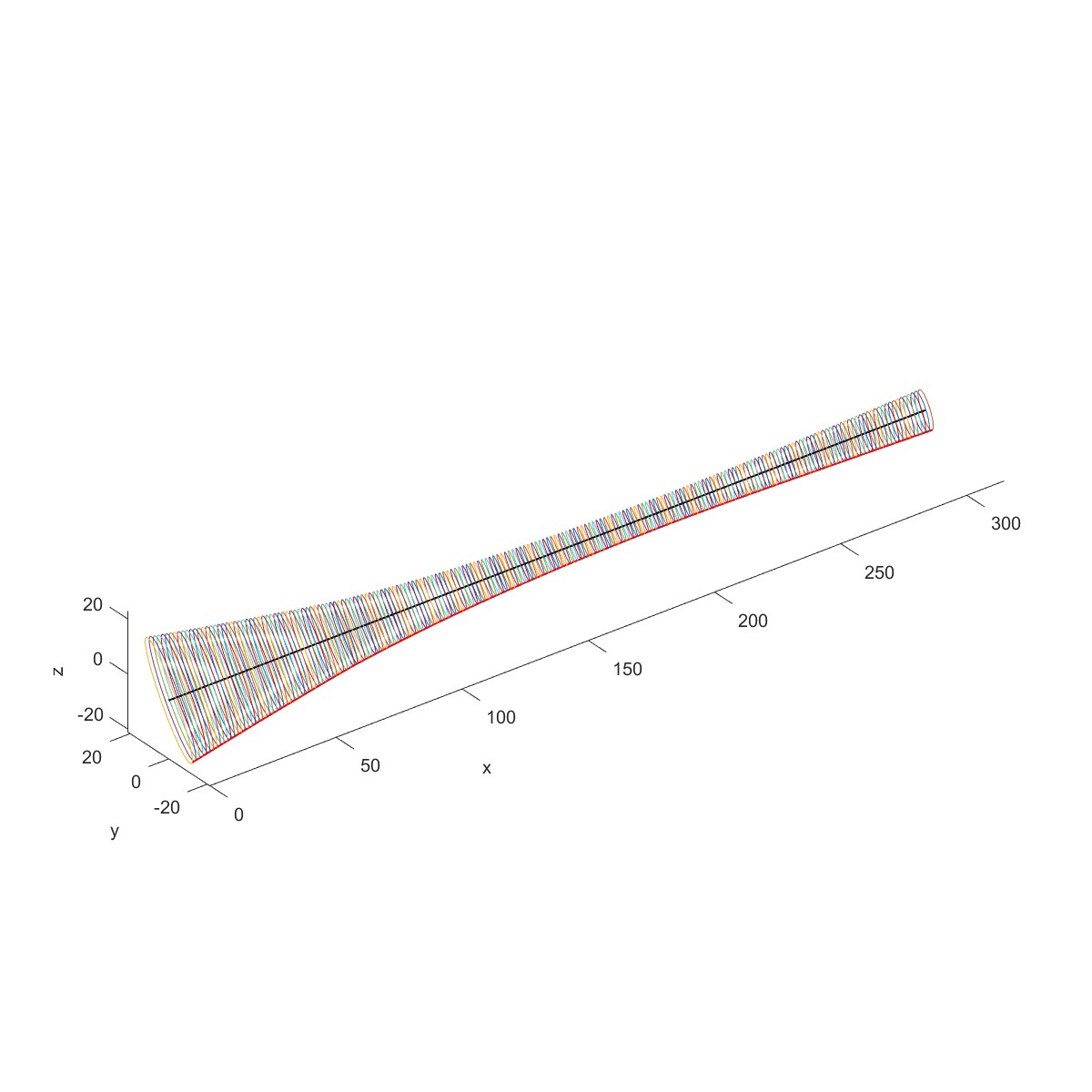
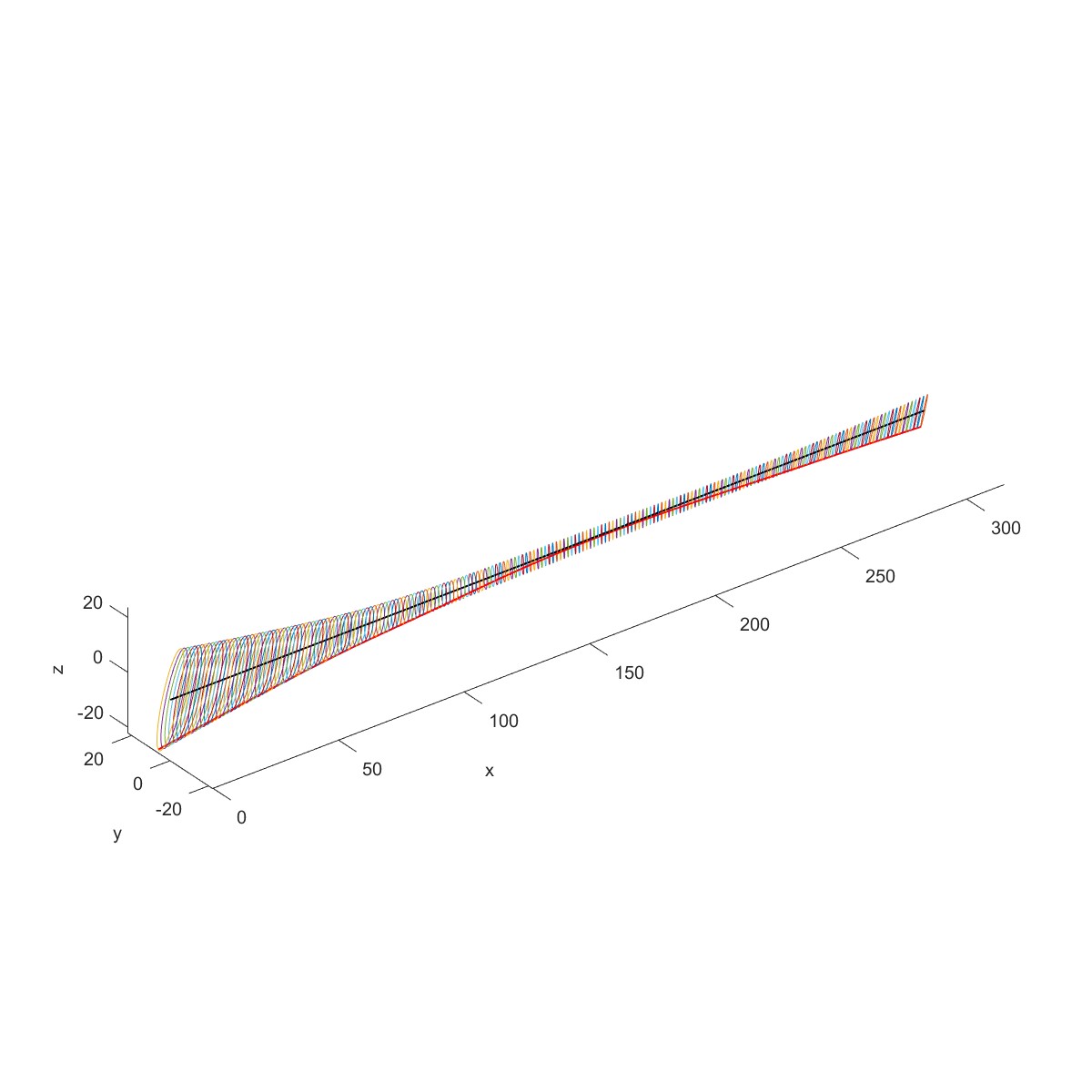
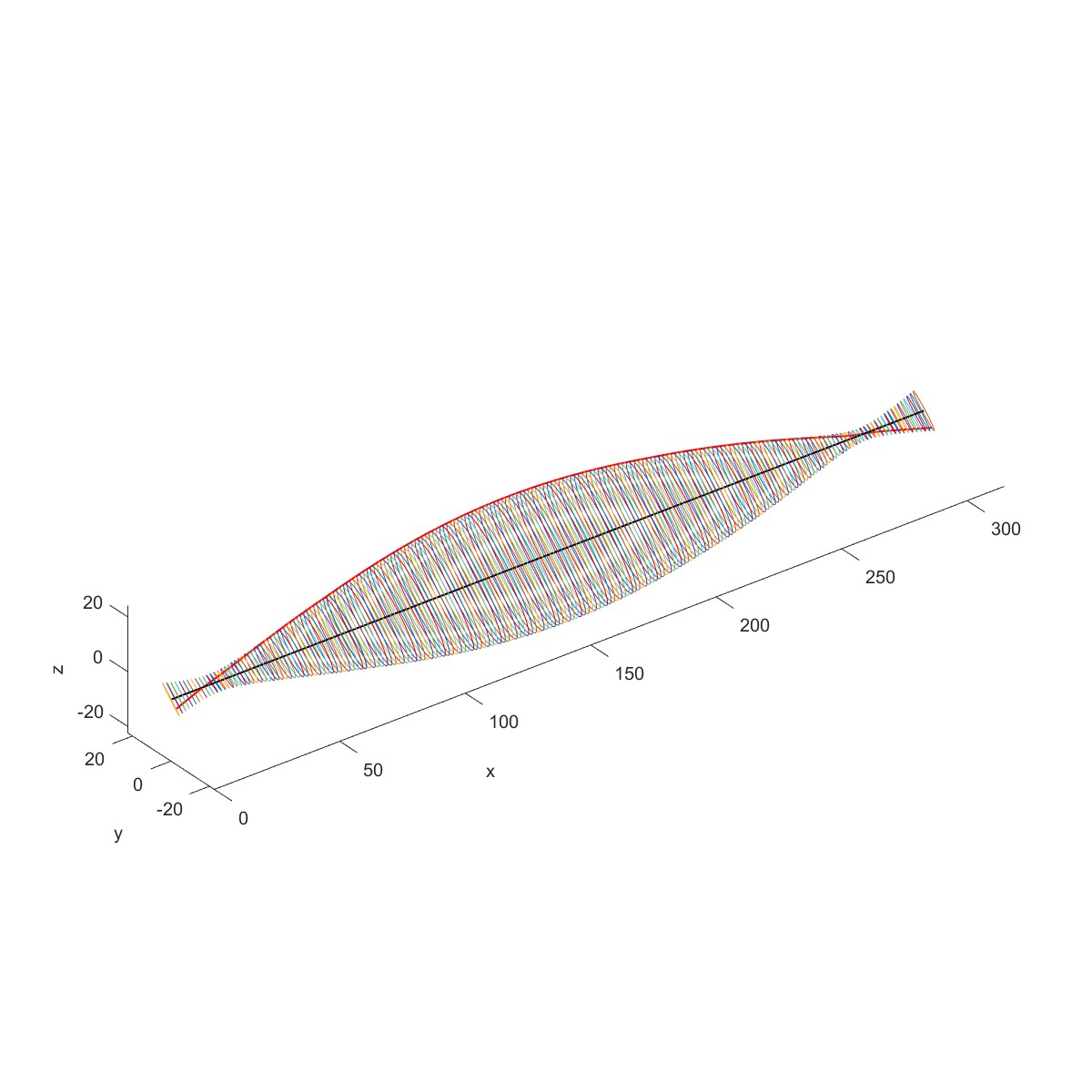
下图为一个工业用的高速机械的转子,工作转速为50000 r/min,转子尺寸如图中所示(单位毫
米)。转子由两个滑动轴承B1、B2支承。两端有两个铝制叶轮D1、D2。
已知有关参数为:
轴的材质为钢,其弹性模量为2.0E11N/m 2 ,质量密度为7800kg/m 3 ,泊桑比为0.3;
B1的油膜刚度系数为 K xx =8E7N/m,K xy =1E7N/m,K yx =6E7N/m,K yy =1E8N/m;
B1的油膜阻尼系数为 C xx =8E3N s/m,C xy =3E3N s/m,C yx =3E3N s/m,C yy =1.2E4N s/m;
B2的油膜刚度系数为 K xx =5E7N/m,K xy =2E7N/m,K yx =4E7N/m,K yy =7E7N/m;
B2的油膜阻尼系数为 C xx =6E3N s/m,C xy =1.5E3N s/m,C yx =1.5E3N s/m,C yy =8E3N s/m;
D1的质量为1.2kg,极转动惯量为2.4 E-3kg m 2 ,直径转动惯量为1.2E-3kg m 2 ;
D2的质量为1.0kg,极转动惯量为2.0E-3kg m 2 ,直径转动惯量为1.0E-3kg m 2 。
% Shaft
inputshaft1.Length = [35;45;70;200;250;300];
inputshaft1.ID = [[0,0];[10,10];[10,10];[10,10];[10,10];[10,10]];
inputshaft1.OD = [[40,40];[70,70];[40,40];[40,40];[40,40];[70,70]];
paramsshaft1.Beam_N = 16;
paramsshaft1.N_Slice=201;
obj1 = shaft.Commonshaft(paramsshaft1, inputshaft1);
obj1 = obj1.solve();
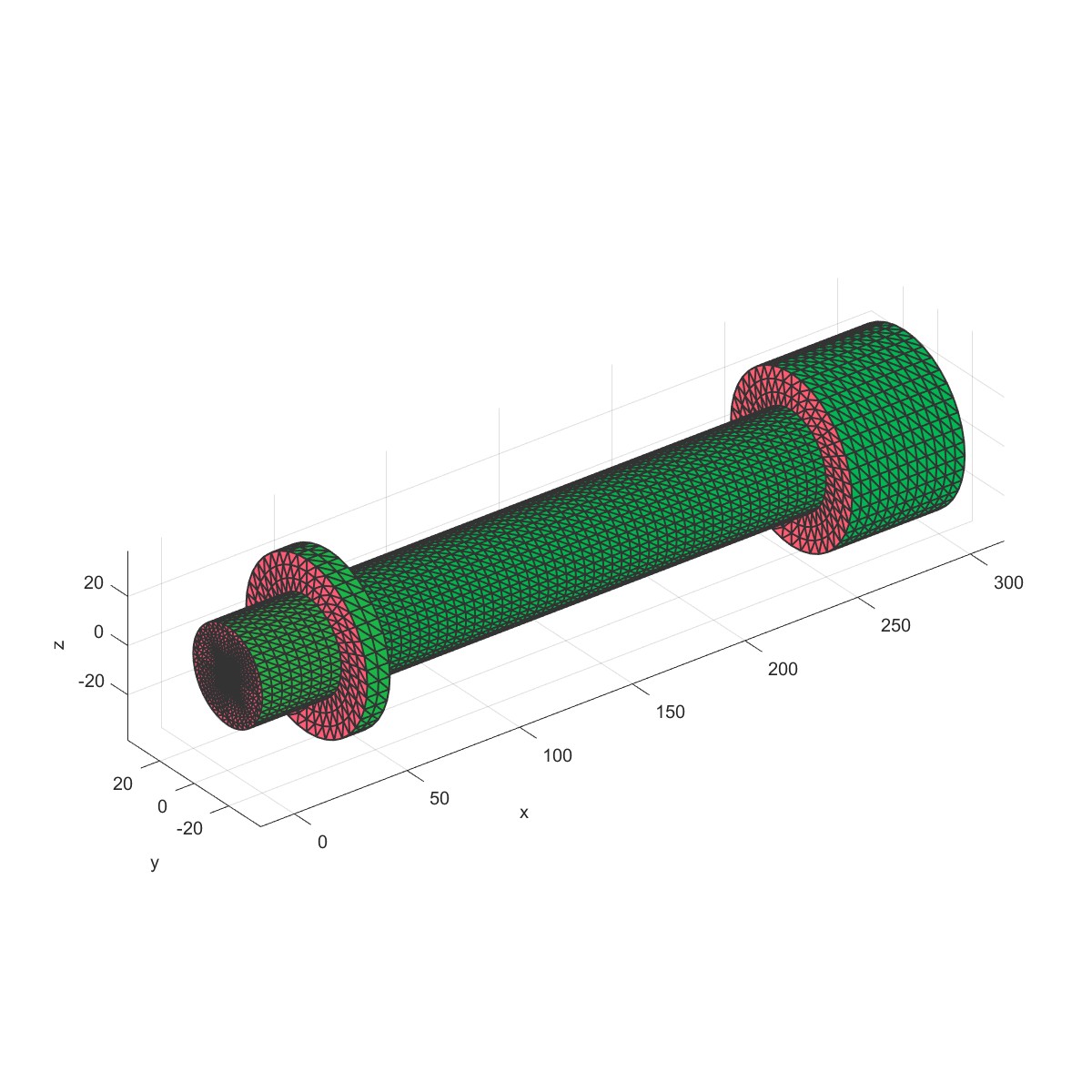
Plot3D(obj1)
mat{1,1}=obj1.params.Material;
inputRotDyn.Shaft=obj1.output.BeamMesh;
inputRotDyn.Speed=[0,10000,20000,30000,40000,50000,60000];
inputRotDyn.PointMass=[1,1.2e-3,2.4,1.2;size(obj1.output.Node,1),1e-3,2,1];
inputRotDyn.MaterialNum=1;
paramsRotDyn.Material=mat;
paramsRotDyn.PrintCampbell=1;
paramsRotDyn.PrintMode=1;
Dyn1 = solve.RotDyn(paramsRotDyn,inputRotDyn);
[Dyn1,Num1]= AddCnode(Dyn1,70);
Dyn1=AddBearing(Dyn1,Num1,[1e10,8e4,1e5,1e4,6e4,0,8,12,3,3]);
[Dyn1,Num2]= AddCnode(Dyn1,200);
Dyn1=AddBearing(Dyn1,Num2,[0,5e4,7e4,2e4,4e4,0,6,8,1.5,1.5]);
Dyn1 = Dyn1.solve();
ANSYSSolve(Dyn1.output.Assembly);
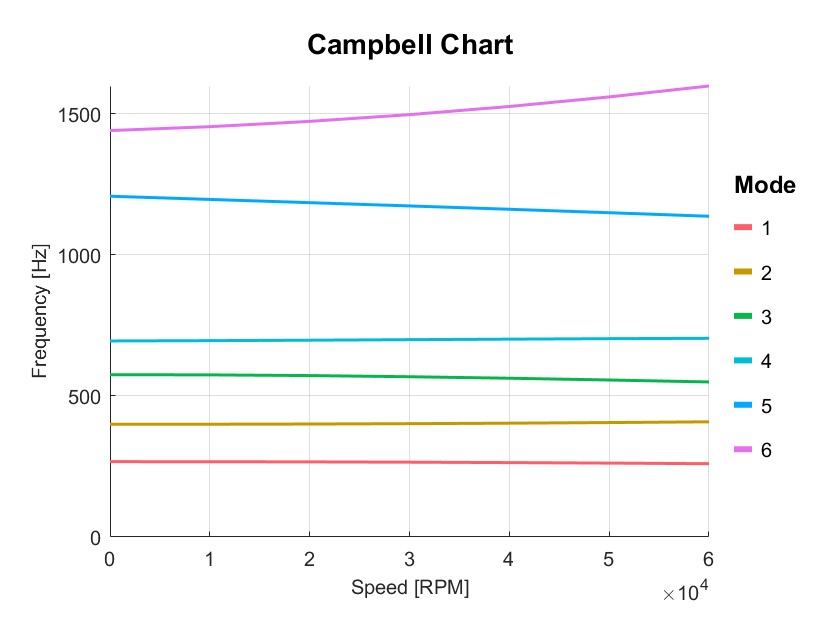
Dyn1=PlotCampbell(Dyn1,'NMode',6);
disp(Dyn1.output.Campbell);
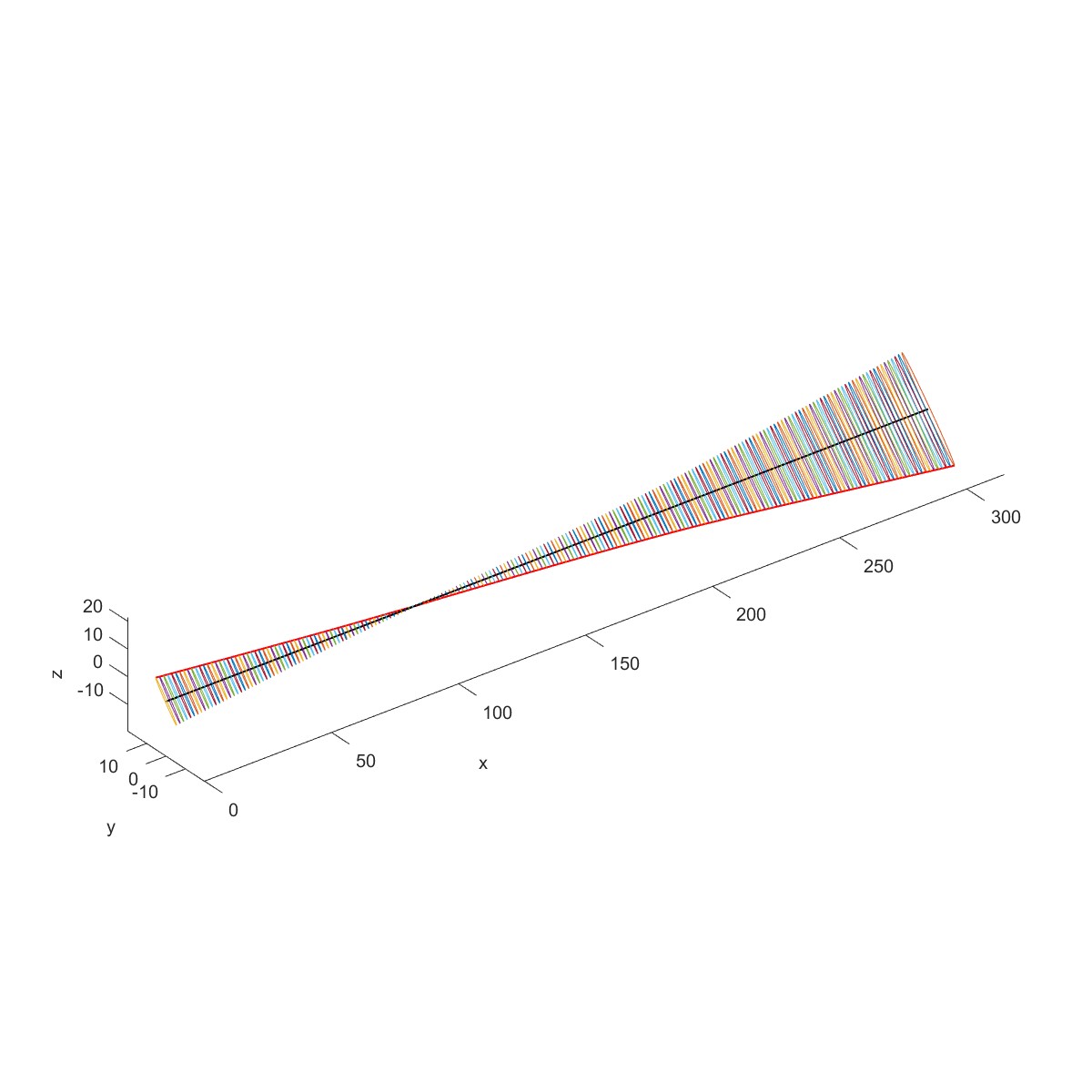
for i=1:6
PlotMode(Dyn1,2,i,'scale',1)
end
Dyn1=CalculateCriticalSpeed(Dyn1);
disp(Dyn1.output.CriticalSpeed);
 |  |
 |  |
 |  |
 |  |
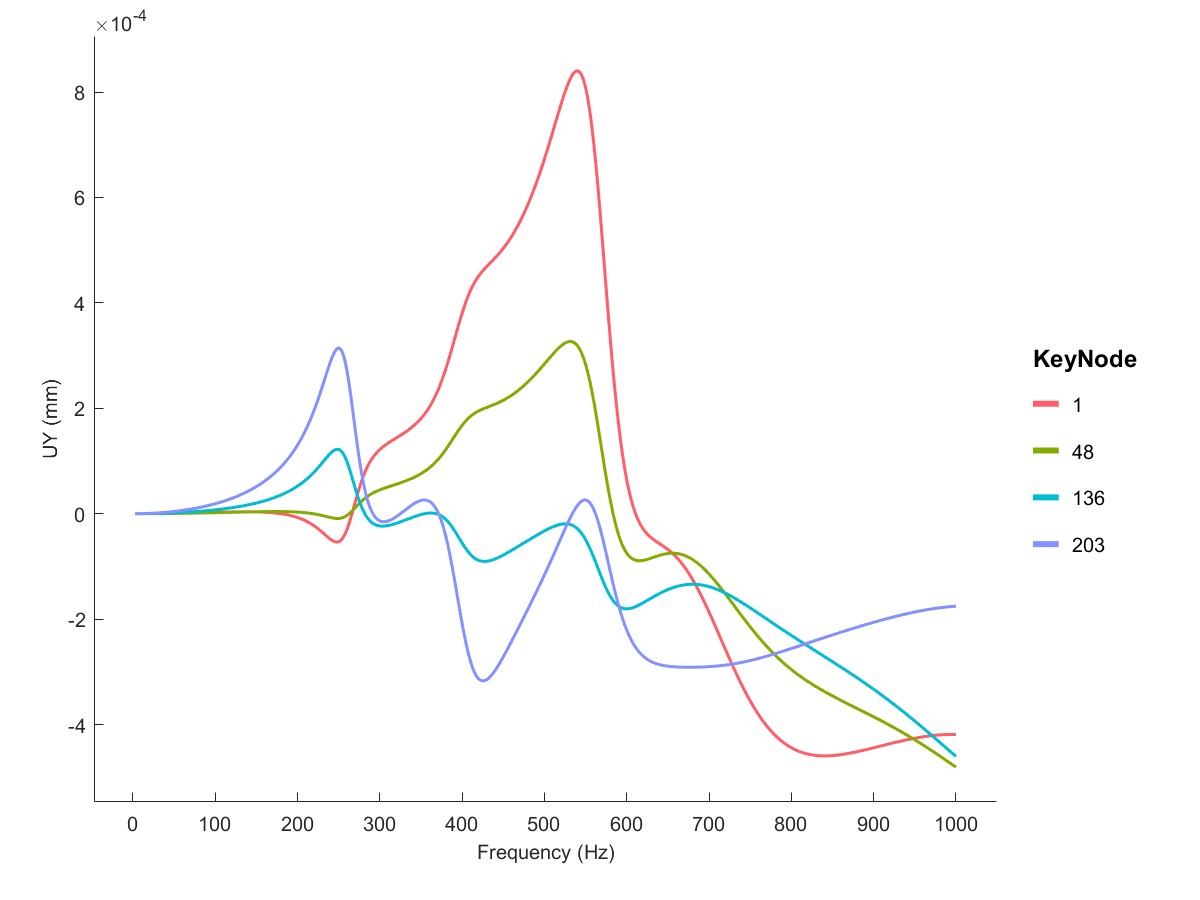
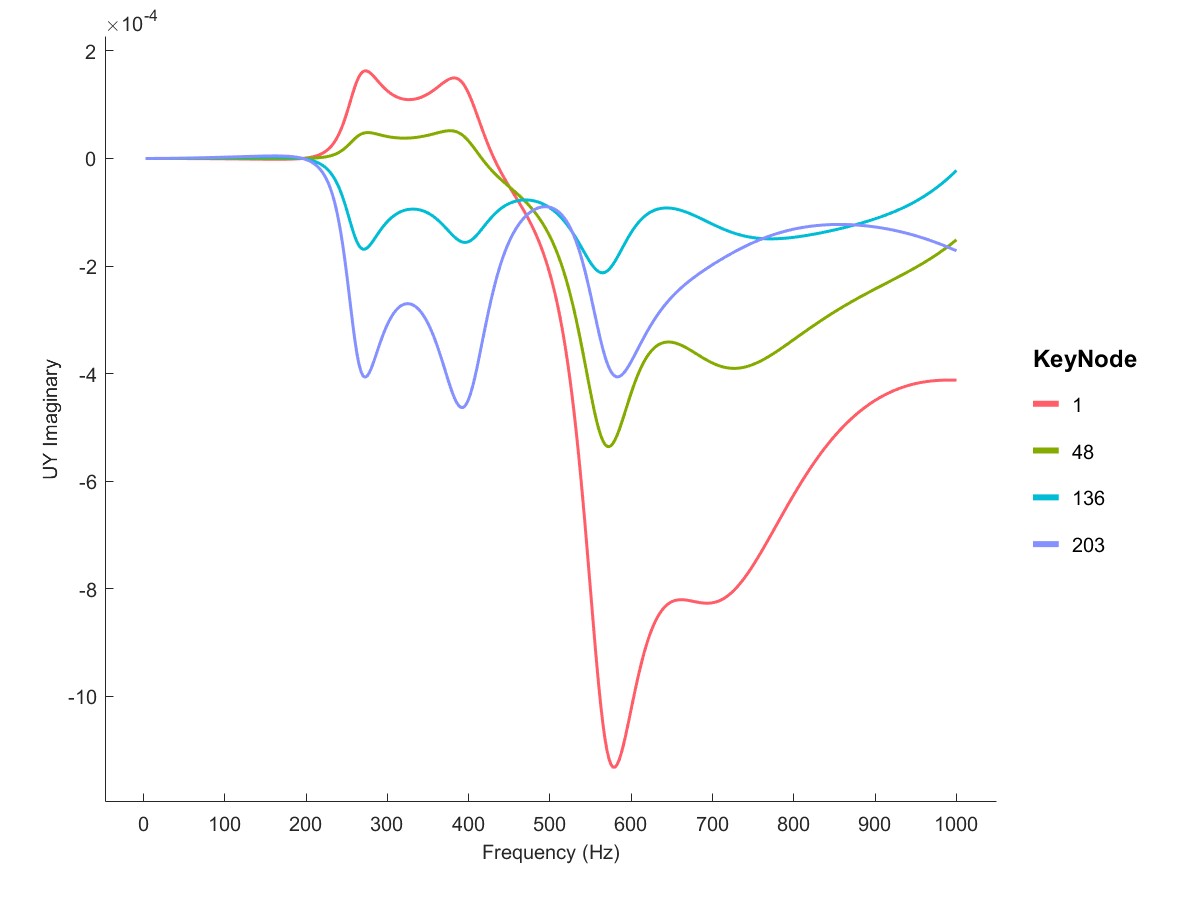
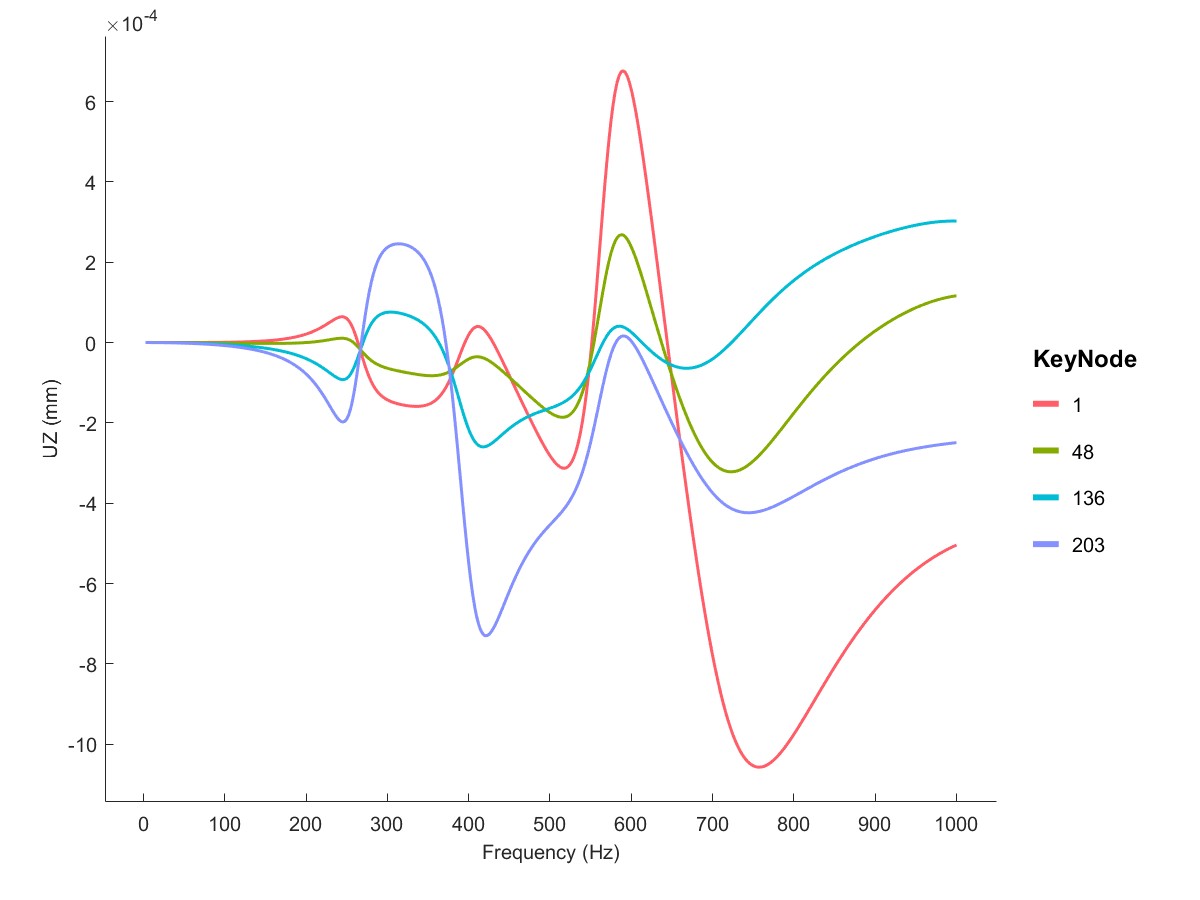
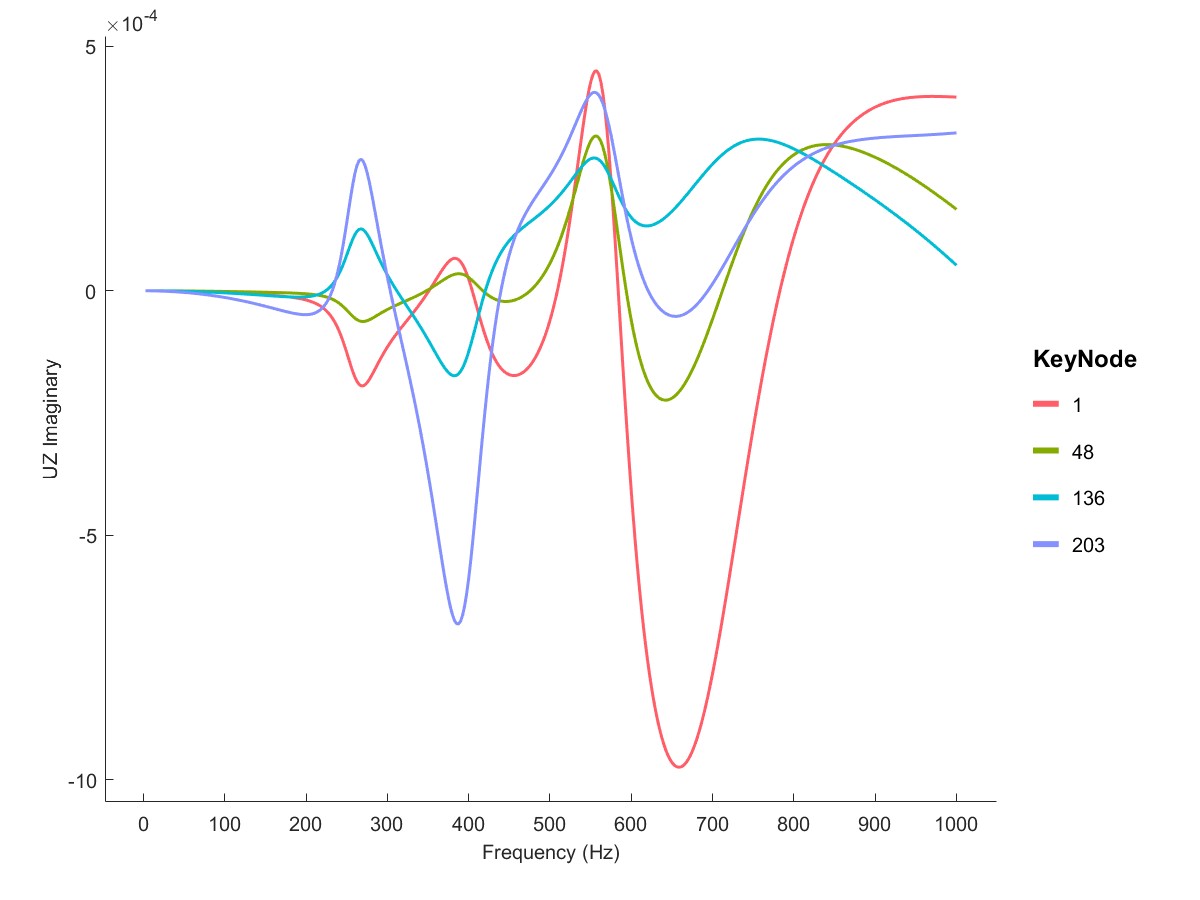
High speed rotor Harmonic analysis (Flag=11)
在高速轴上施加me=0.5e-6 Nmm的不平衡量,进行谐响应分析,可以观察此时轴节点的谐响应。
% Shaft
inputshaft1.Length = [35;45;70;200;250;300];
inputshaft1.ID = [[0,0];[10,10];[10,10];[10,10];[10,10];[10,10]];
inputshaft1.OD = [[40,40];[70,70];[40,40];[40,40];[40,40];[70,70]];
paramsshaft1.Beam_N = 16;
paramsshaft1.N_Slice=201;
obj1 = shaft.Commonshaft(paramsshaft1, inputshaft1);
obj1 = obj1.solve();
Plot3D(obj1)
mat{1,1}=obj1.params.Material;
inputRotDyn.Shaft=obj1.output.BeamMesh;
inputRotDyn.Speed=[0,10000,20000,30000,40000,50000,60000];
inputRotDyn.PointMass=[1,1.2e-3,2.4,1.2;size(obj1.output.Node,1),1e-3,2,1];
inputRotDyn.UnBalanceForce=[1,0.5e-6;size(obj1.output.Node,1),0.5e-6];
inputRotDyn.MaterialNum=1;
paramsRotDyn.Material=mat;
paramsRotDyn.Type=3;
Dyn1 = solve.RotDyn(paramsRotDyn,inputRotDyn);
[Dyn1,Num1]= AddCnode(Dyn1,70);
Dyn1=AddBearing(Dyn1,Num1,[1e10,8e4,1e5,1e4,6e4,0,8,12,3,3]);
[Dyn1,Num2]= AddCnode(Dyn1,200);
Dyn1=AddBearing(Dyn1,Num2,[0,5e4,7e4,2e4,4e4,0,6,8,1.5,1.5]);
Dyn1 = Dyn1.solve();
ANSYSSolve(Dyn1.output.Assembly);
PlotSpeedup(Dyn1);
 |  |
 |  |
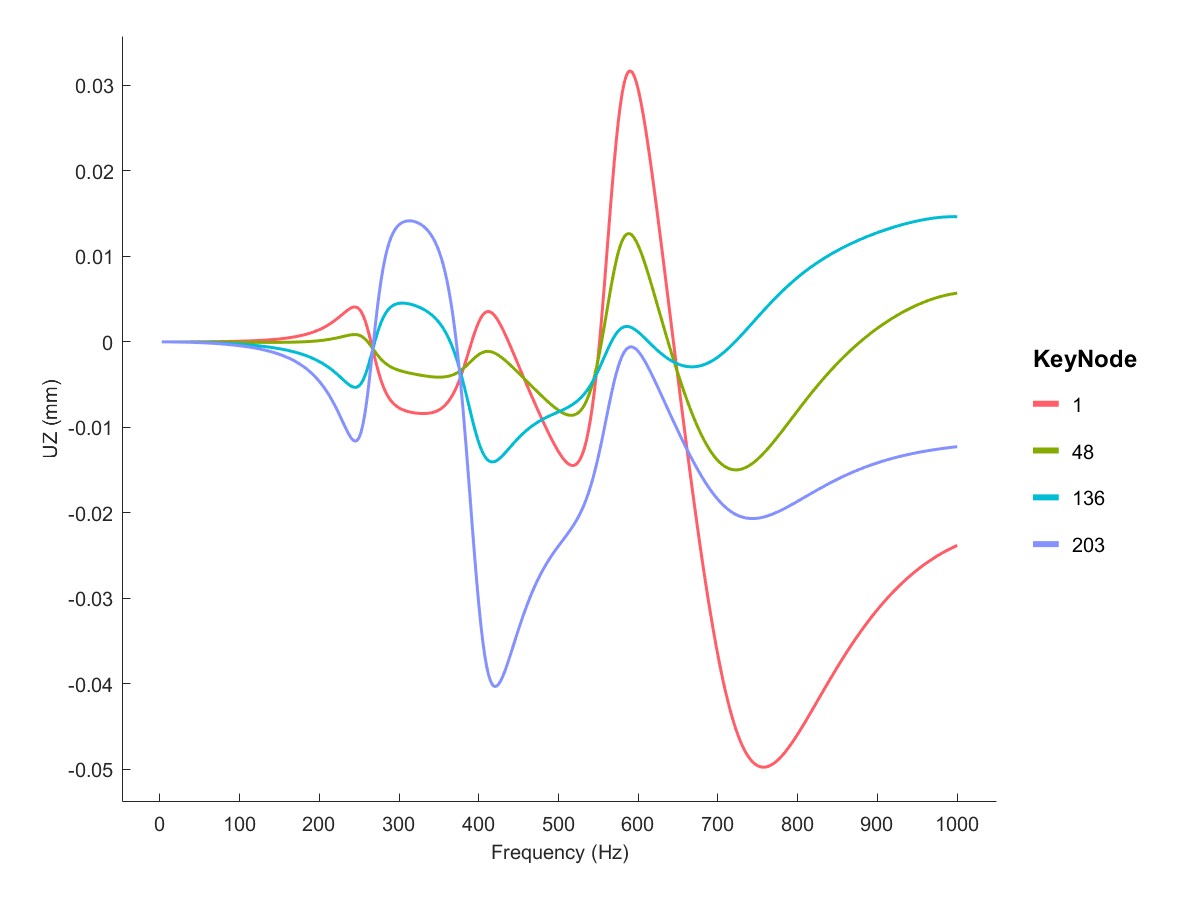
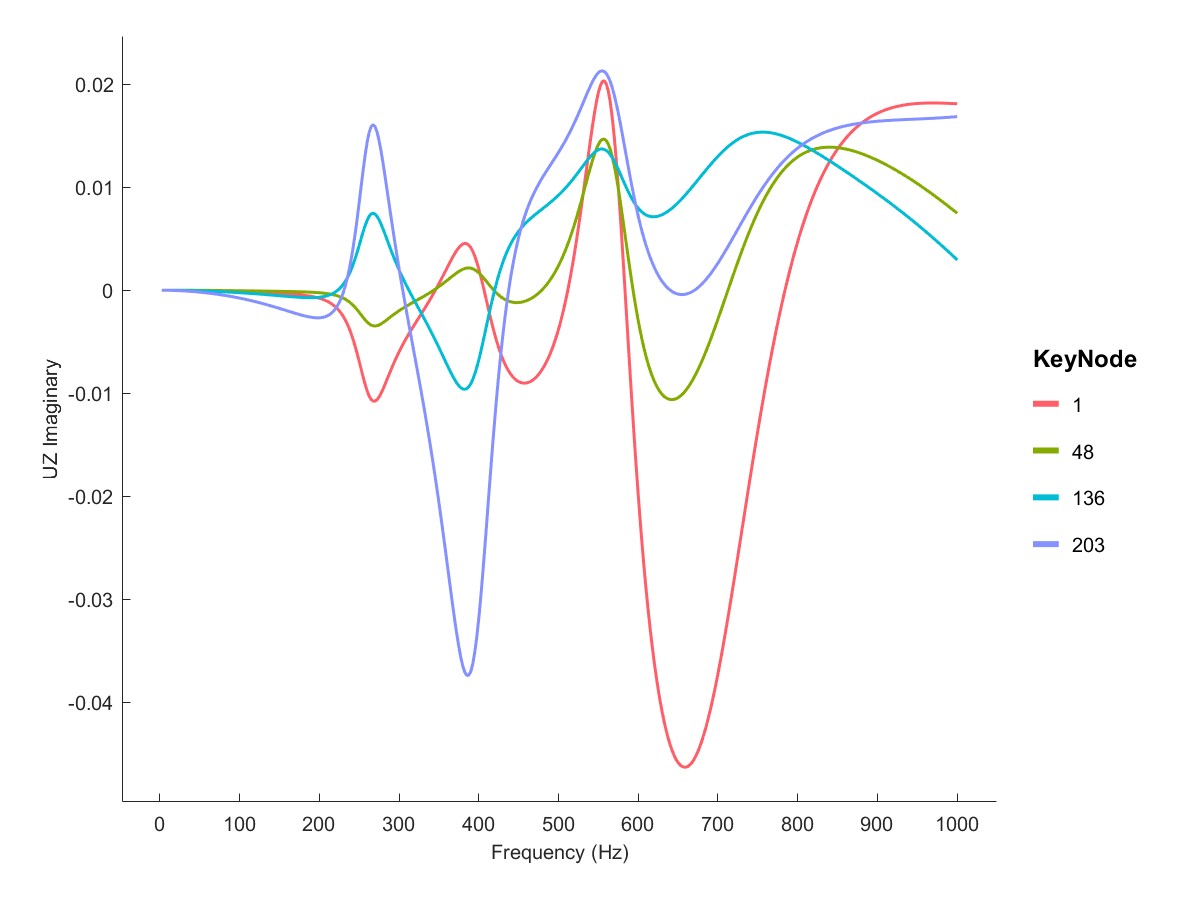
High speed unbalance (Flag=12)
如果输入平衡质量,RotDyn会计算轴的重心,根据ISO1940标准计算平衡盘上的不平衡载荷,如下所示,设置平衡质量G=2.5,平衡转速为3000RPM,得到的谐响应如下。
% Shaft
inputshaft1.Length = [35;45;70;200;250;300];
inputshaft1.ID = [[0,0];[10,10];[10,10];[10,10];[10,10];[10,10]];
inputshaft1.OD = [[40,40];[70,70];[40,40];[40,40];[40,40];[70,70]];
paramsshaft1.Beam_N = 16;
paramsshaft1.N_Slice=201;
obj1 = shaft.Commonshaft(paramsshaft1, inputshaft1);
obj1 = obj1.solve();
Plot3D(obj1)
mat{1,1}=obj1.params.Material;
inputRotDyn.Shaft=obj1.output.BeamMesh;
inputRotDyn.Speed=[0,10000,20000,30000,40000,50000,60000];
inputRotDyn.PointMass=[1,1.2e-3,2.4,1.2;size(obj1.output.Node,1),1e-3,2,1];
inputRotDyn.MaterialNum=1;
inputRotDyn.BalanceQuality=[2.5,3000,0,300,0];
paramsRotDyn.Material=mat;
paramsRotDyn.Type=3;
Dyn1 = solve.RotDyn(paramsRotDyn,inputRotDyn);
[Dyn1,Num1]= AddCnode(Dyn1,70);
Dyn1=AddBearing(Dyn1,Num1,[1e10,8e4,1e5,1e4,6e4,0,8,12,3,3]);
[Dyn1,Num2]= AddCnode(Dyn1,200);
Dyn1=AddBearing(Dyn1,Num2,[0,5e4,7e4,2e4,4e4,0,6,8,1.5,1.5]);
Dyn1 = Dyn1.solve();
ANSYSSolve(Dyn1.output.Assembly);
PlotSpeedup(Dyn1);
 |  |
 |  |
Rotor FRF analysis (Flag=13)
% Shaft
inputshaft1.Length = 500;
inputshaft1.ID = [0,0];
inputshaft1.OD = [8,8];
paramsshaft1.Beam_N = 16;
paramsshaft1.N_Slice=10;
obj1 = shaft.Commonshaft(paramsshaft1, inputshaft1);
obj1 = obj1.solve();
Plot3D(obj1)
mat{1,1}=obj1.params.Material;
inputRotDyn.Shaft=obj1.output.BeamMesh;
inputRotDyn.Speed=0;
inputRotDyn.MaterialNum=1;
paramsRotDyn.Material=mat;
paramsRotDyn.Type=1;
paramsRotDyn.Solver='Local';
paramsRotDyn.Rayleigh=[1e-5,10];
Dyn1 = solve.RotDyn(paramsRotDyn,inputRotDyn);
Dyn1 = AddBCNode(Dyn1,1,[1,1,1,1,1,1]);
[Dyn1,Num1]= AddCnode(Dyn1,500);
[Dyn1,Num2]= AddCnode(Dyn1,250);
Dyn1 = AddBearing(Dyn1,Num1,[0,1e2,1e2,0,0,0,0,0,0,0]);
Dyn1 = AddInNode(Dyn1,Num1);
Dyn1 = AddOutNode(Dyn1,[Num1;Num2]);
Dyn1 = Dyn1.solve();
PlotBode(Dyn1)
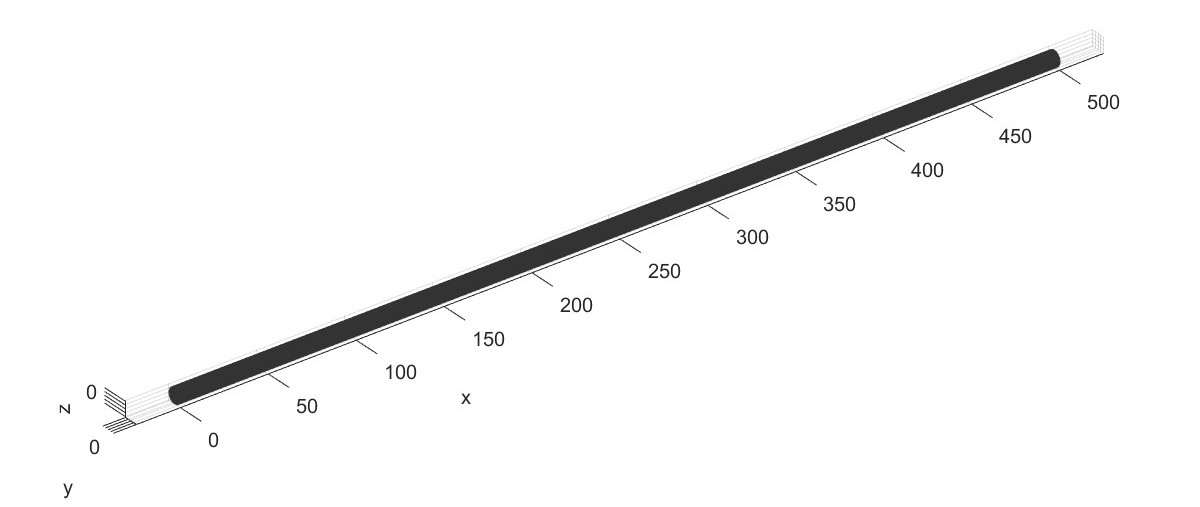
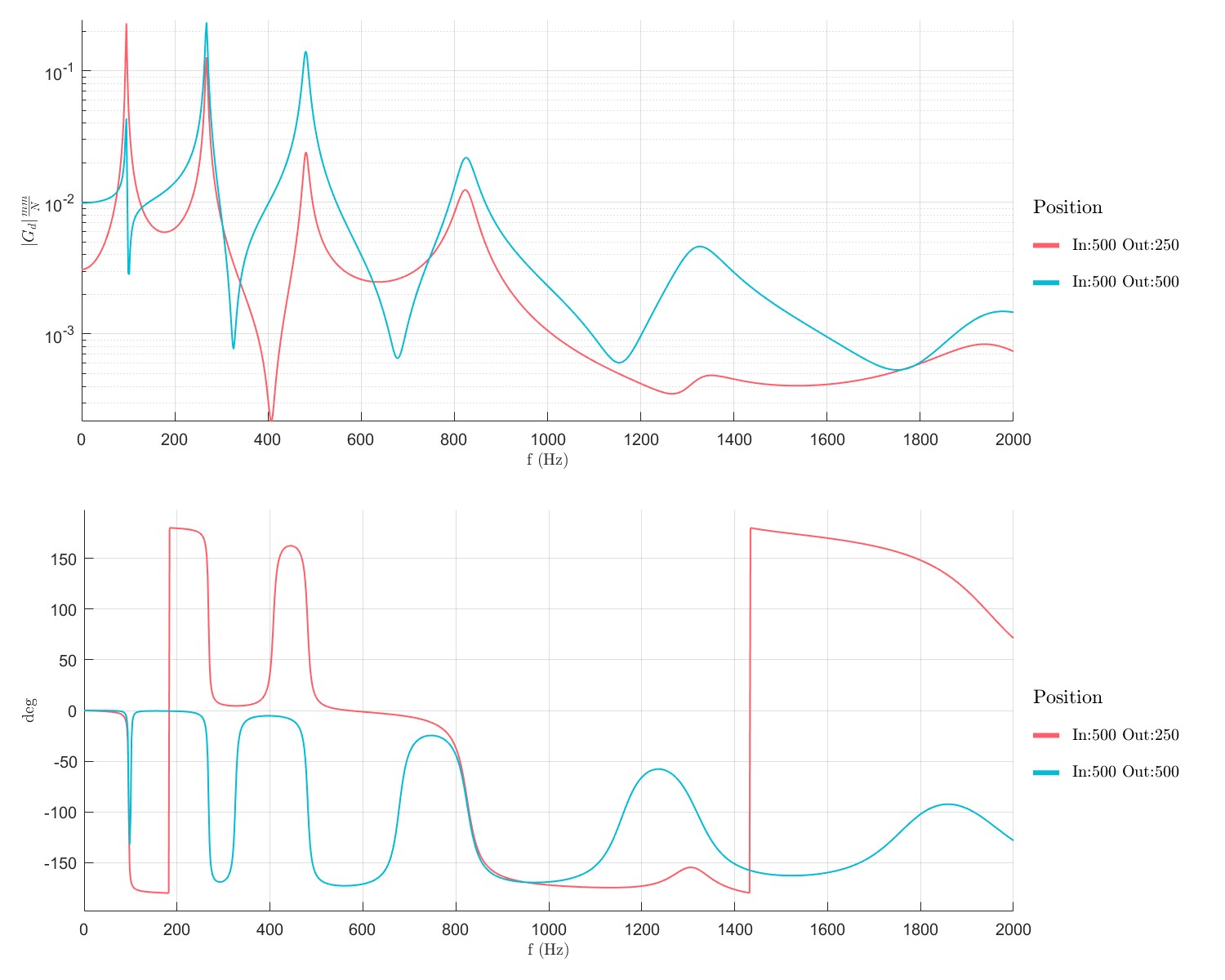
Rotor modal analysis with loacl solver (Flag=14)
% Shaft
inputshaft1.Length = 500;
inputshaft1.ID = [0,0];
inputshaft1.OD = [8,8];
paramsshaft1.Beam_N = 16;
paramsshaft1.N_Slice=10;
obj1 = shaft.Commonshaft(paramsshaft1, inputshaft1);
obj1 = obj1.solve();
Plot3D(obj1)
mat{1,1}=obj1.params.Material;
inputRotDyn.Shaft=obj1.output.BeamMesh;
inputRotDyn.Speed=0;
inputRotDyn.MaterialNum=1;
paramsRotDyn.Material=mat;
paramsRotDyn.Type=2;
paramsRotDyn.PrintMode=1;
paramsRotDyn.PrintCampbell=1;
paramsRotDyn.Solver='Local';
% paramsRotDyn.Rayleigh=[0,0];
paramsRotDyn.Rayleigh=[1e-5,10];
Dyn1 = solve.RotDyn(paramsRotDyn,inputRotDyn);
Dyn1 = AddBCNode(Dyn1,1,[1,1,1,1,1,1]);
[Dyn1,Num1]= AddCnode(Dyn1,500);
Dyn1 = AddBearing(Dyn1,Num1,[0,1e2,1e2,0,0,0,0,0,0,0]);
Dyn1 = Dyn1.solve();
for i=1:10
PlotMode(Dyn1,1,i,'scale',5)
end
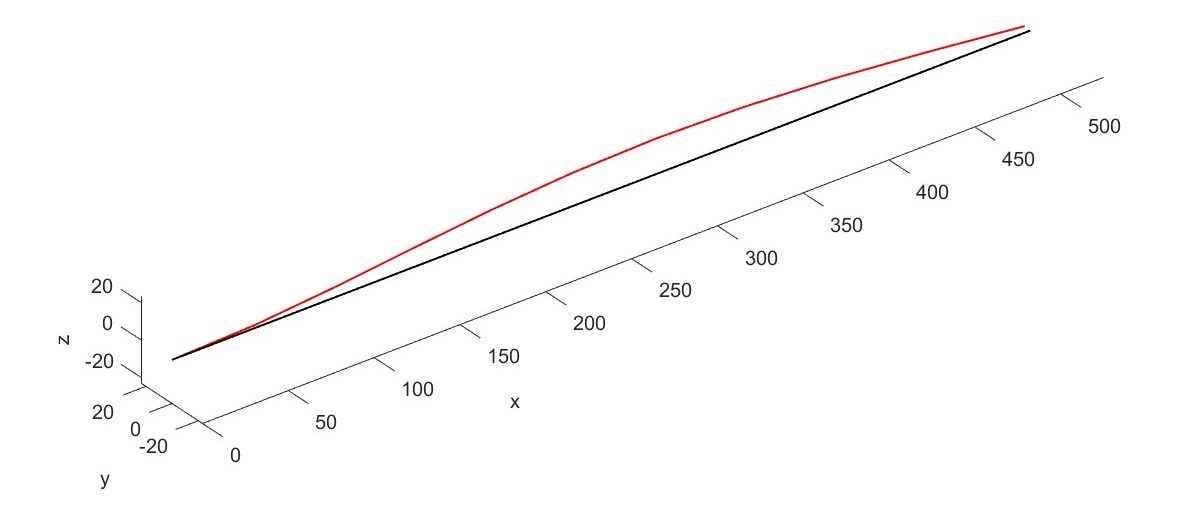
Rotor campbell analysis with loacl solver (Flag=15)
% Shaft
inputshaft1.Length = 500;
inputshaft1.ID = [0,0];
inputshaft1.OD = [8,8];
paramsshaft1.Beam_N = 16;
paramsshaft1.N_Slice=10;
obj1 = shaft.Commonshaft(paramsshaft1, inputshaft1);
obj1 = obj1.solve();
Plot3D(obj1)
mat{1,1}=obj1.params.Material;
inputRotDyn.Shaft=obj1.output.BeamMesh;
inputRotDyn.Speed=(0:1000:10000);
inputRotDyn.MaterialNum=1;
paramsRotDyn.Material=mat;
paramsRotDyn.Type=2;
paramsRotDyn.PrintMode=1;
paramsRotDyn.PrintCampbell=1;
paramsRotDyn.Solver='Local';
% paramsRotDyn.Rayleigh=[0,0];
paramsRotDyn.Rayleigh=[1e-5,10];
Dyn1 = solve.RotDyn(paramsRotDyn,inputRotDyn);
Dyn1 = AddBCNode(Dyn1,1,[1,1,1,1,1,1]);
[Dyn1,Num1]= AddCnode(Dyn1,500);
Dyn1 = AddBearing(Dyn1,Num1,[0,1e2,1e2,0,0,0,0,0,0,0]);
Dyn1 = Dyn1.solve();
Dyn1=PlotCampbell(Dyn1,'NMode',8);
disp(Dyn1.output.Campbell);
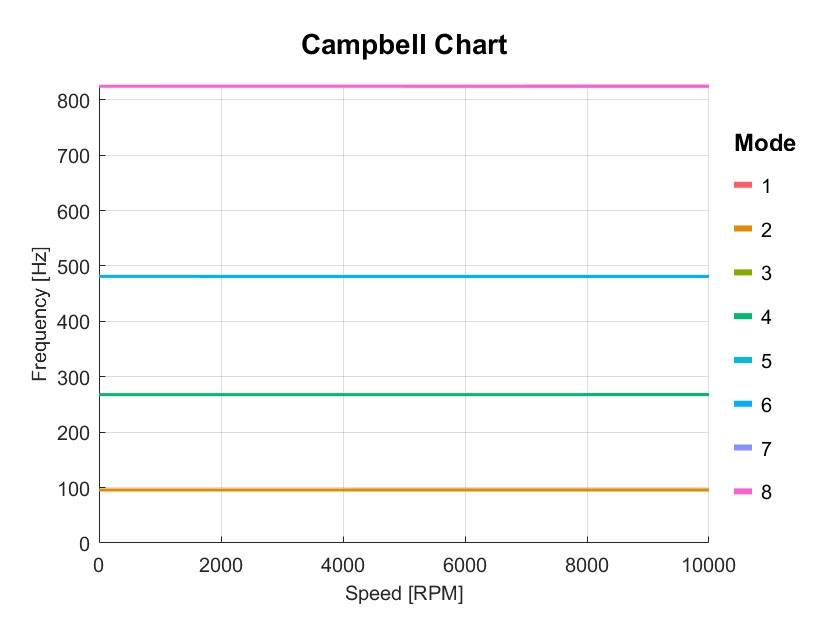
Num Status rpm1 rpm2 rpm3 rpm4 rpm5 rpm6 rpm7 rpm8 rpm9 rpm10 rpm11
1 “FW” 95.744 95.747 95.749 95.751 95.754 95.756 95.758 95.761 95.763 95.766 95.768
2 “BW” 95.744 95.742 95.739 95.737 95.735 95.732 95.73 95.728 95.725 95.723 95.72
3 “FW” 267.82 267.82 267.83 267.84 267.84 267.85 267.86 267.86 267.87 267.87 267.88
4 “BW” 267.82 267.81 267.81 267.8 267.79 267.79 267.78 267.77 267.77 267.76 267.76
5 “FW” 481.07 481.08 481.1 481.12 481.14 481.16 481.18 481.19 481.21 481.23 481.25
6 “BW” 481.07 481.05 481.03 481.01 480.99 480.97 480.96 480.94 480.92 480.9 480.88
7 “FW” 824.32 824.36 824.4 824.43 824.47 824.51 824.55 824.58 824.62 824.66 824.7
8 “BW” 824.32 824.28 824.24 824.21 824.17 824.13 824.09 824.06 824.02 823.98 823.94
9 “FW” 1318.9 1319 1319 1319.1 1319.2 1319.2 1319.3 1319.3 1319.4 1319.5 1319.5
10 “BW” 1318.9 1318.9 1318.8 1318.7 1318.7 1318.6 1318.6 1318.5 1318.4 1318.4 1318.3
11 “FW” 1949.5 1949.6 1949.7 1949.8 1949.9 1950 1950 1950.1 1950.2 1950.3 1950.4
12 “BW” 1949.5 1949.4 1949.3 1949.3 1949.2 1949.1 1949 1948.9 1948.8 1948.7 1948.7
Rotor stationary analysis with constant speed (Flag=16)
转子在给定转速下的时序分析。
% Shaft
inputshaft1.Length = 500;
inputshaft1.ID = [0,0];
inputshaft1.OD = [8,8];
paramsshaft1.Beam_N = 16;
paramsshaft1.N_Slice=10;
Shaft = shaft.Commonshaft(paramsshaft1, inputshaft1);
Shaft = Shaft.solve();
Plot3D(Shaft)
% Load
inputStruct2.Time=0:1e-3:1;
inputStruct2.Fy=rand(1,length(inputStruct2.Time));
paramsStruct2=struct();
Load=signal.ForceLoad(paramsStruct2, inputStruct2);
Load=Load.solve();
Plot(Load);
mat{1,1}=Shaft.params.Material;
inputRotDyn.Shaft=Shaft.output.BeamMesh;
inputRotDyn.Speed=(0:1000:2000);
inputRotDyn.MaterialNum=1;
paramsRotDyn.Material=mat;
paramsRotDyn.Type=4;
paramsRotDyn.PrintMode=1;
paramsRotDyn.PrintCampbell=1;
paramsRotDyn.Solver='Local';
% paramsRotDyn.Rayleigh=[0,0];
paramsRotDyn.Rayleigh=[1e-5,10];
Dyn1 = solve.RotDyn(paramsRotDyn,inputRotDyn);
Dyn1 = AddBCNode(Dyn1,1,[1,1,1,1,1,1]);
[Dyn1,Num1]= AddCnode(Dyn1,500);
[Dyn1,Num2]= AddCnode(Dyn1,250);
Dyn1 = AddBearing(Dyn1,Num1,[0,1e2,1e2,0,0,0,0,0,0,0]);
Dyn1 = AddTimeSeries(Dyn1,Num2,Load.output.Load);
Dyn1 = Dyn1.solve();
PlotTimeSeriesResult(Dyn1,'Node',Dyn1.input.KeyNode,'Component',[1;2],'Load',1);
不同点的位移、速度和加速度如下所示:
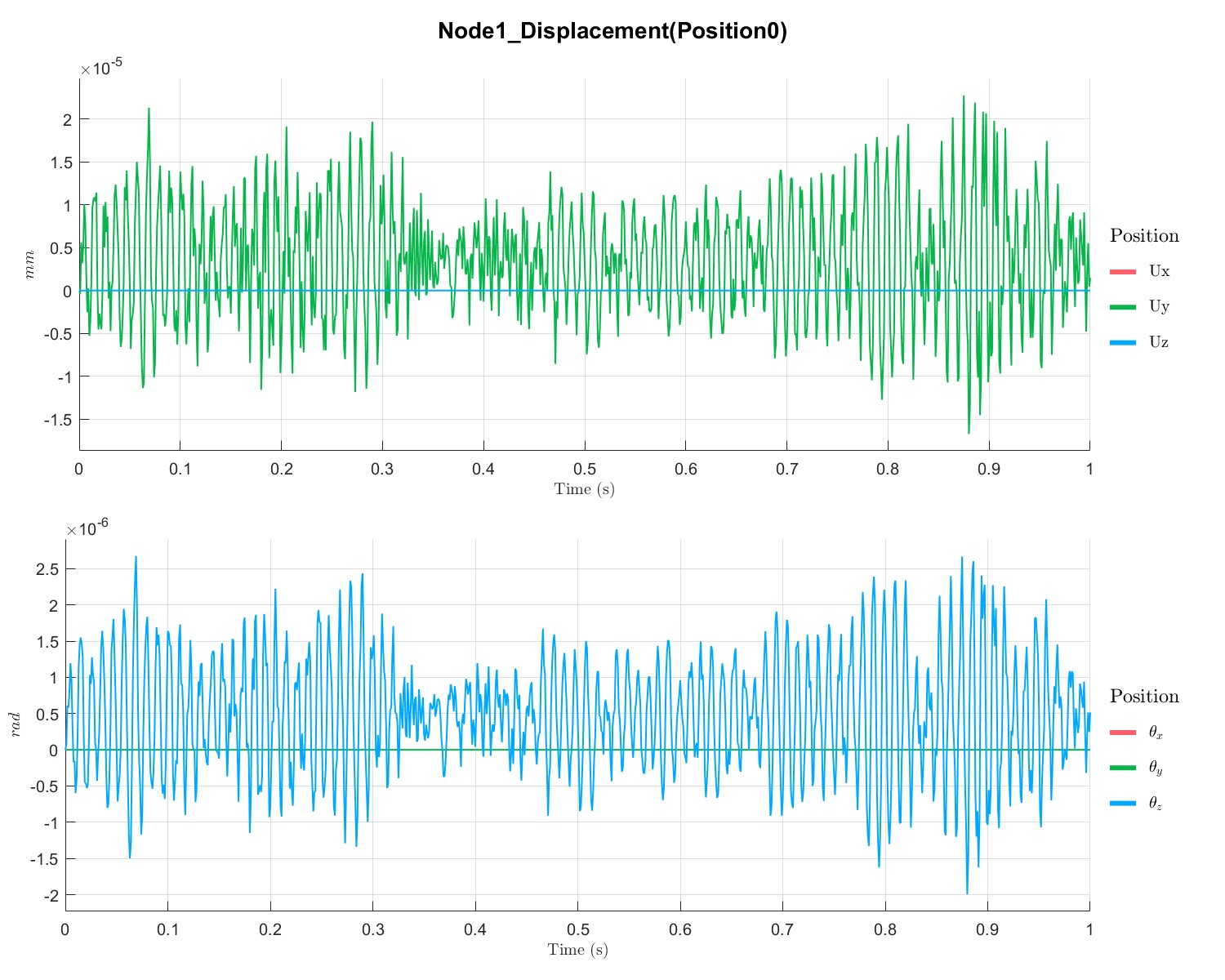
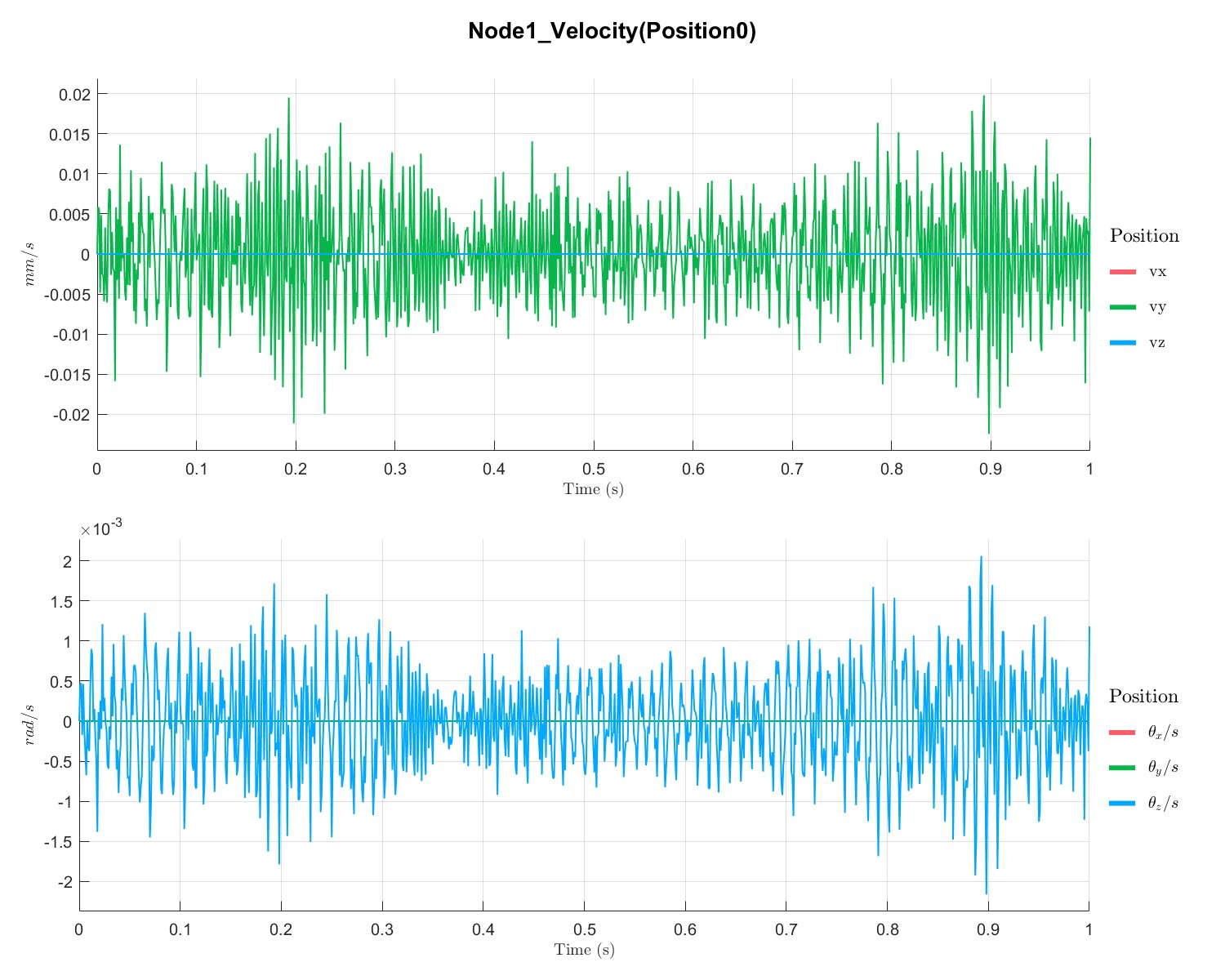
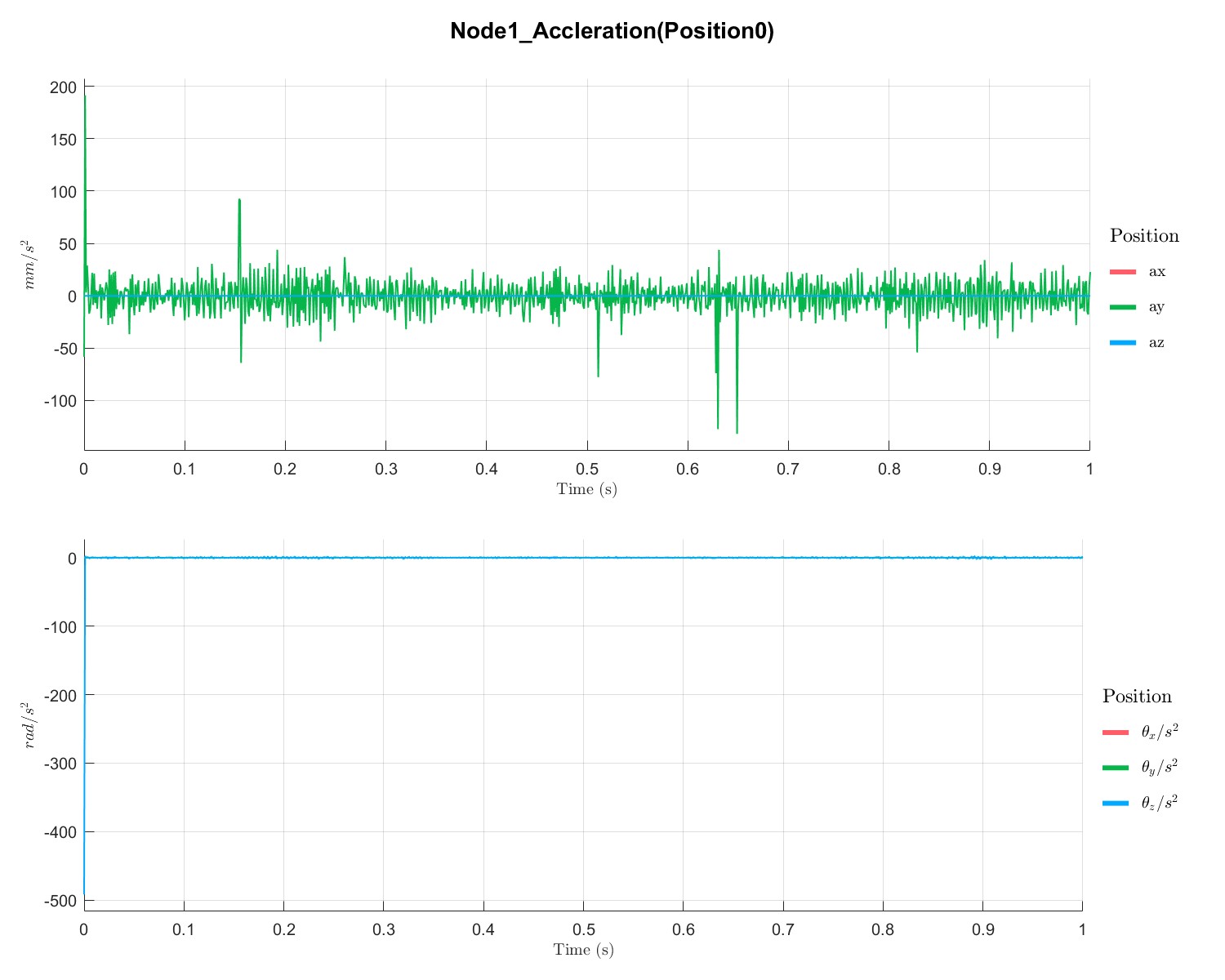
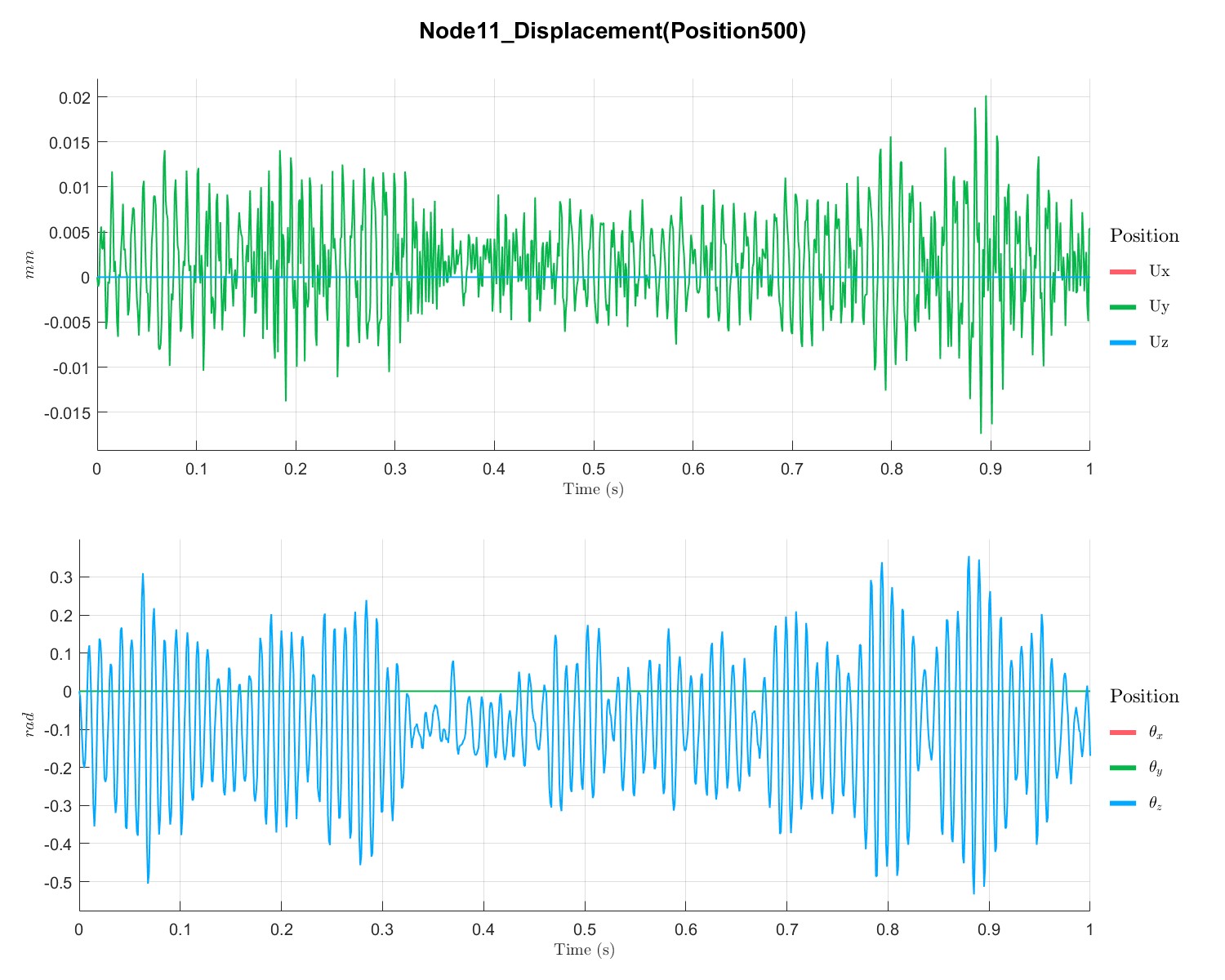
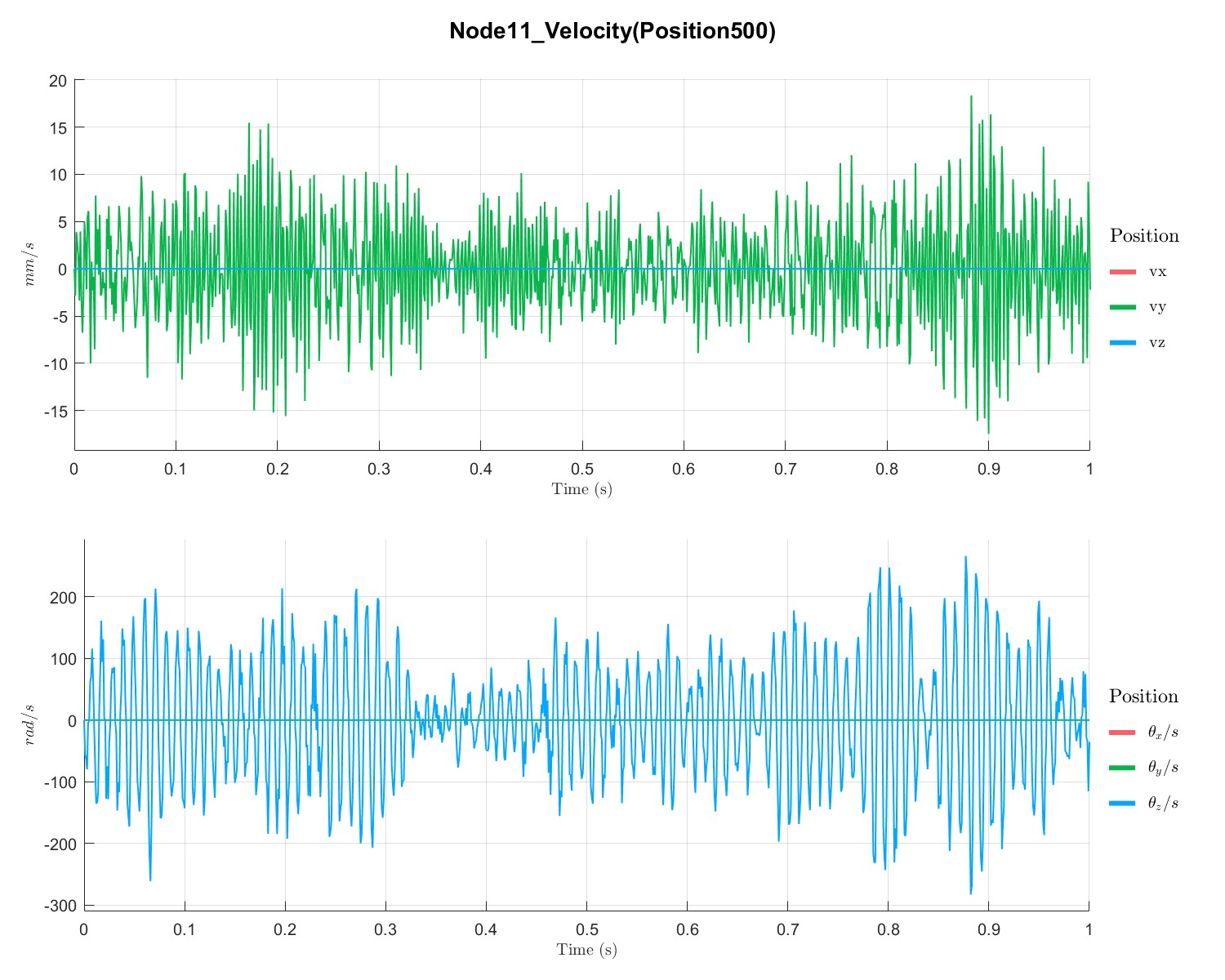
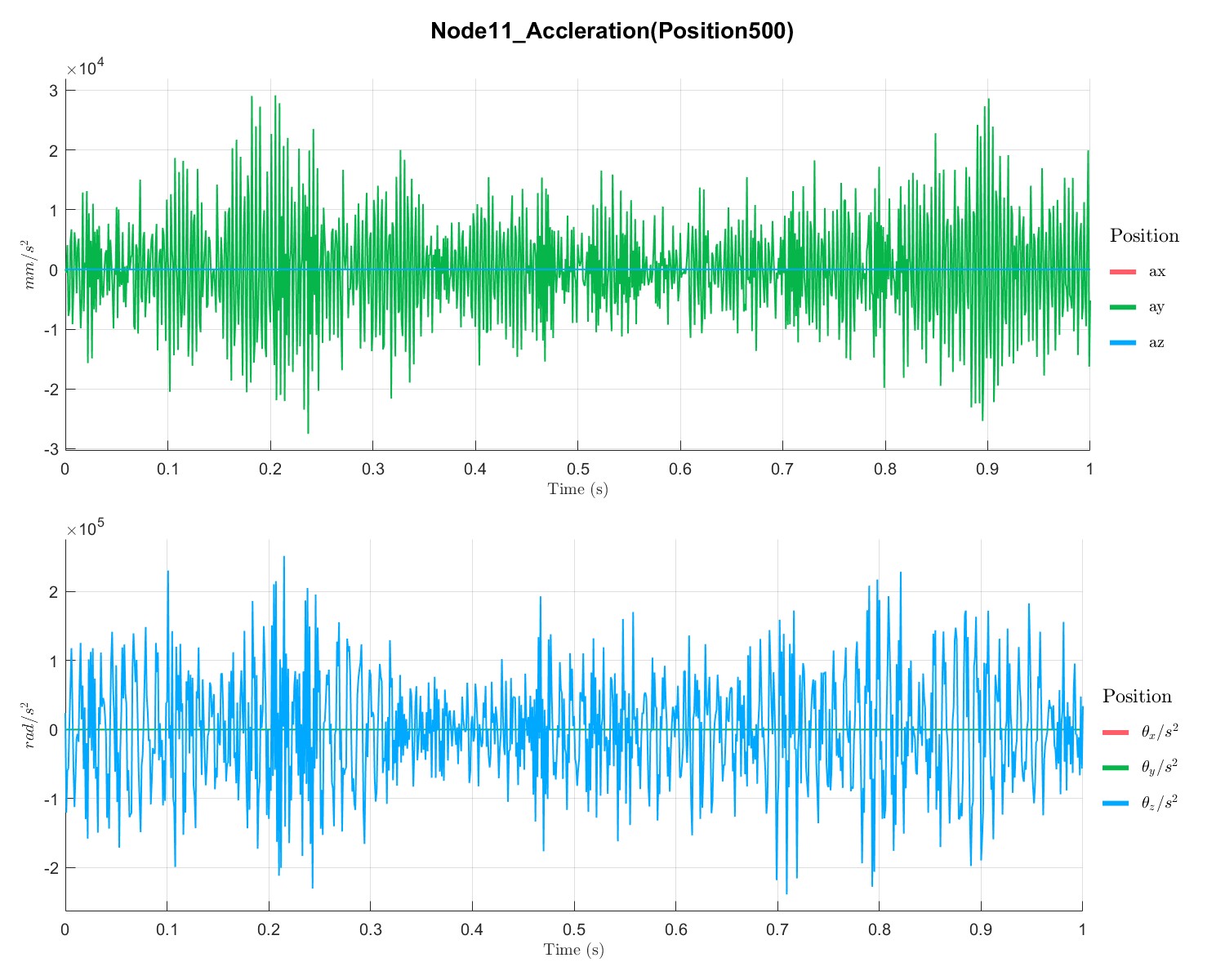
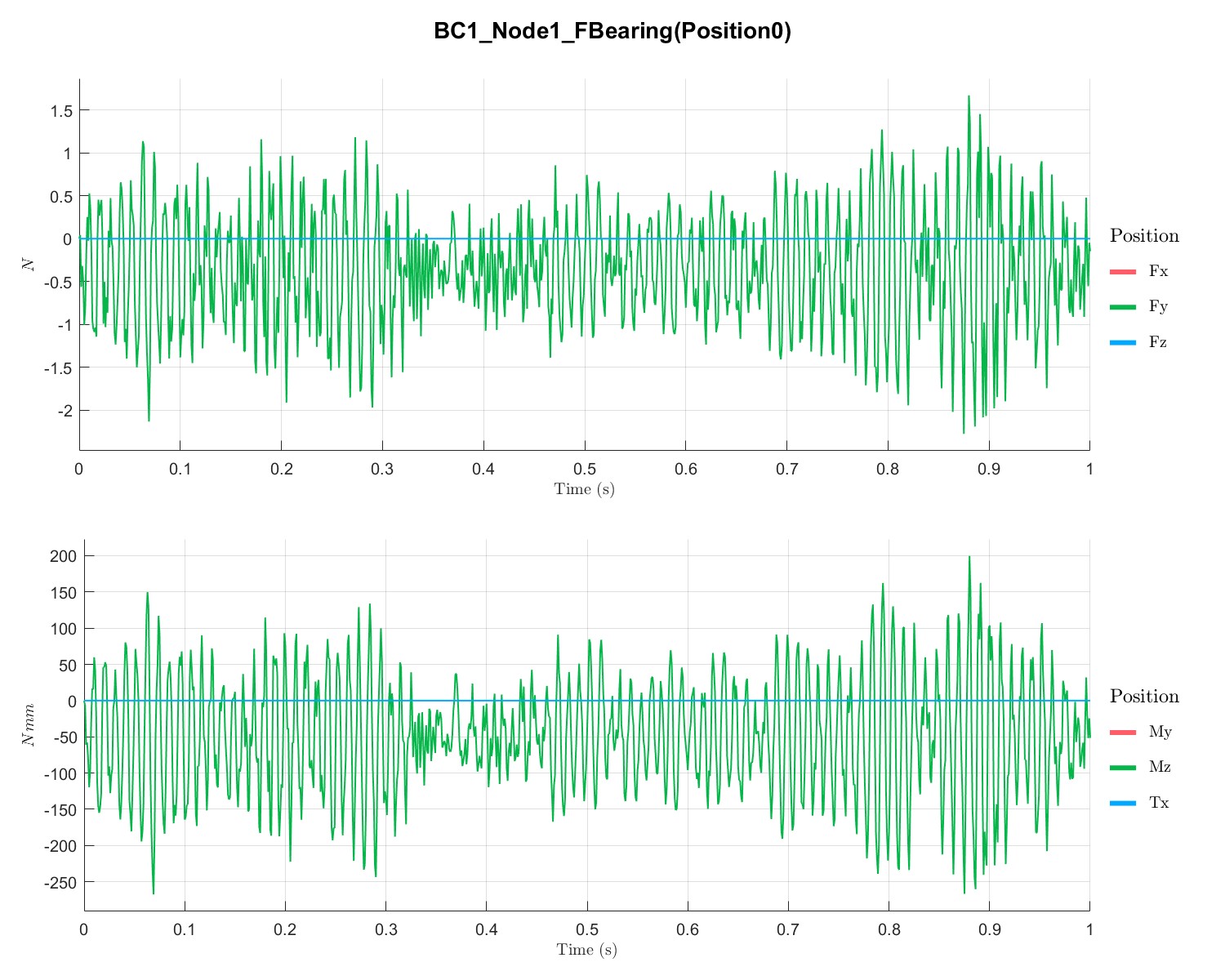
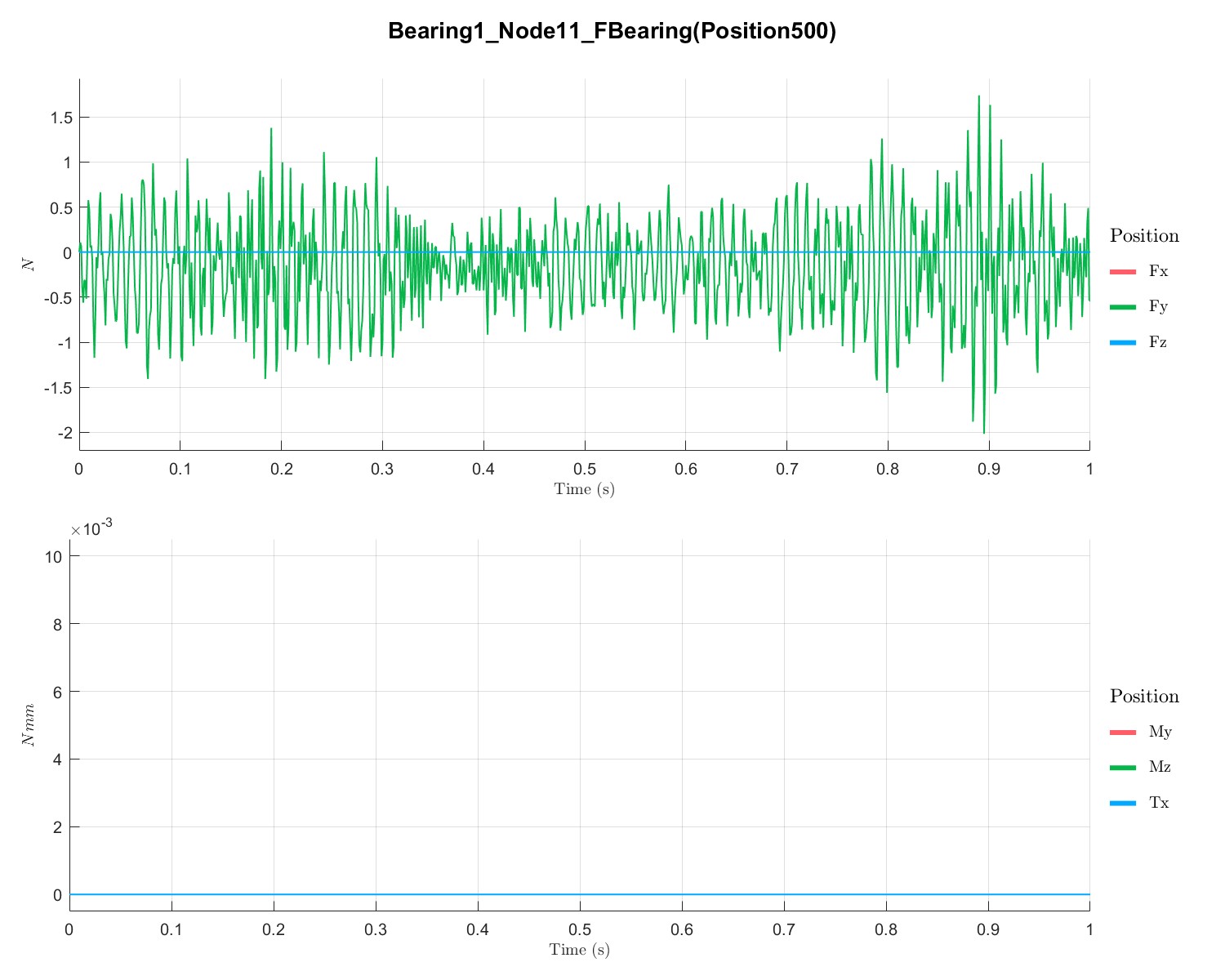
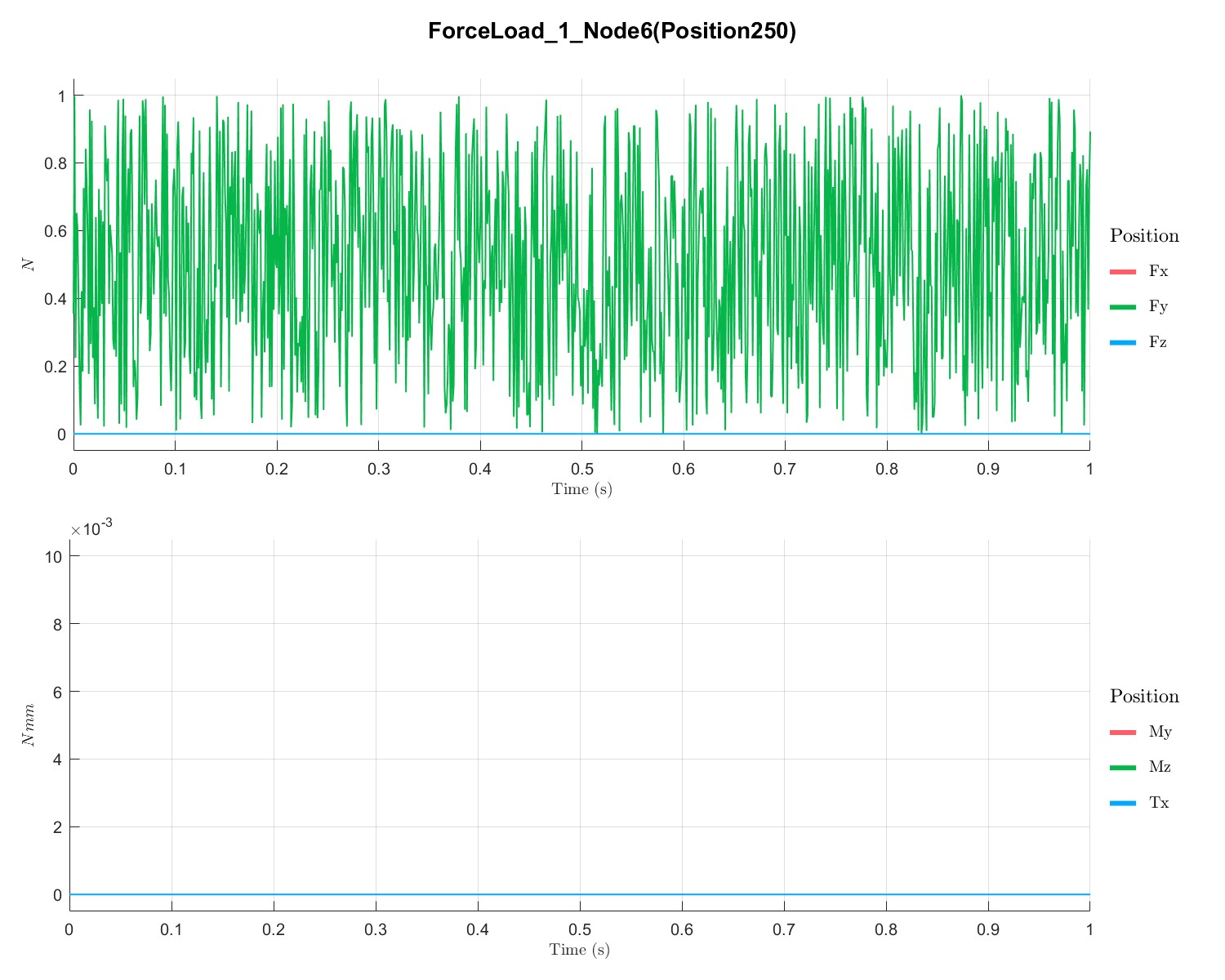
Rotor with disc campbell analysis with local solver (Flag=17)
% Shaft
inputshaft1.Length = [118;158;215;345;402;442;580];
inputshaft1.ID = [[0,0];[0,0];[0,0];[0,0];[0,0];[0,0];[0,0]];
inputshaft1.OD = [[16,16];[17.6,17.6];[16,16];[17.6,17.6];[16,16];[17.6,17.6];[16,16]];
paramsshaft1.Beam_N = 16;
paramsshaft1.N_Slice=118;
Shaft = shaft.Commonshaft(paramsshaft1, inputshaft1);
Shaft = Shaft.solve();
Plot3D(Shaft)
mat{1,1}=Shaft.params.Material;
inputRotDyn.Shaft=Shaft.output.BeamMesh;
inputRotDyn.Speed=(1000:1000:8000);
inputRotDyn.MaterialNum=1;
paramsRotDyn.Material=mat;
paramsRotDyn.Type=2;
paramsRotDyn.PrintMode=1;
paramsRotDyn.PrintCampbell=1;
paramsRotDyn.Solver='Local';
% paramsRotDyn.Rayleigh=[0,0];
paramsRotDyn.Rayleigh=[1.69e-5,16.04];% 0.001
Dyn1 = solve.RotDyn(paramsRotDyn,inputRotDyn);
[Dyn1,Num1]= AddCnode(Dyn1,9);
[Dyn1,Num2]= AddCnode(Dyn1,138);
[Dyn1,Num3]= AddCnode(Dyn1,422);
[Dyn1,Num4]= AddCnode(Dyn1,551);
Dyn1=AddPointMass(Dyn1,Num1,1.056e-4,2.4649e-2,1.6004e-2);
Dyn1=AddPointMass(Dyn1,Num2,4.207e-4,1.3102e-2,1.2324e-2);
Dyn1=AddPointMass(Dyn1,Num3,4.207e-4,1.3102e-2,1.2324e-2);
Dyn1=AddPointMass(Dyn1,Num4,1.056e-4,2.4649e-2,1.6004e-2);
nEle=28;
Step=(345-215)/(nEle-1);
[Dyn1,Num]= AddCnode(Dyn1,215);
Dyn1=AddPointMass(Dyn1,Num,2.01e-5,7.0059e-3,3.3452e-3);
for i=2:nEle-1
[Dyn1,Num]= AddCnode(Dyn1,215+(i-1)*Step);
Dyn1=AddPointMass(Dyn1,Num,2.01e-5,7.0059e-3,3.3452e-3);
[Dyn1,Num]= AddCnode(Dyn1,215+(i-1)*Step);
Dyn1=AddPointMass(Dyn1,Num,2.01e-5,7.0059e-3,3.3452e-3);
end
[Dyn1,Num]= AddCnode(Dyn1,345);
Dyn1=AddPointMass(Dyn1,Num,2.01e-5,7.0059e-3,3.3452e-3);
Dyn1=AddBearing(Dyn1,1,[1e7,0,0,0,0,0,0,0,0,0]); % Axial bearing
[Dyn1,Num1]= AddCnode(Dyn1,9);
Dyn1=AddTorBearing(Dyn1,Num1,[1e13,0]);% Torsional bearing
Dyn1=AddBearing(Dyn1,Num1,[0,2e5,2e5,0,0,0,0,0,0,0]);% Simple bearing
[Dyn1,Num4]= AddCnode(Dyn1,551);
Dyn1=AddBearing(Dyn1,Num4,[0,2e5,2e5,0,0,0,0,0,0,0]);% Simple bearing
% LUTBearing
load TestRigLam1Ecc0.mat %#ok<LOAD>
RPM=rpm';
K11=stiffness_matrix{1,1}/1000; %#ok<USENS>
K22=stiffness_matrix{2,2}/1000;
K12=stiffness_matrix{1,2}/1000;
K21=stiffness_matrix{2,1}/1000;
C11=damping_matrix{1, 1}/1000; %#ok<USENS>
C22=damping_matrix{2, 2}/1000;
C12=damping_matrix{1, 2}/1000;
C21=damping_matrix{2, 1}/1000;
LUTBearing1=table(RPM,K11,K22,K12,K21,C11,C22,C12,C21);
Dyn1=AddTable(Dyn1,LUTBearing1);
% LUTBearing
load TestRigLam2Ecc0.mat %#ok<LOAD>
RPM=rpm';
K11=stiffness_matrix{1,1}/1000;
K22=stiffness_matrix{2,2}/1000;
K12=stiffness_matrix{1,2}/1000;
K21=stiffness_matrix{2,1}/1000;
C11=damping_matrix{1, 1}/1000;
C22=damping_matrix{2, 2}/1000;
C12=damping_matrix{1, 2}/1000;
C21=damping_matrix{2, 1}/1000;
LUTBearing2=table(RPM,K11,K22,K12,K21,C11,C22,C12,C21);
Dyn1=AddTable(Dyn1,LUTBearing2);
[Dyn1,Num]= AddCnode(Dyn1,250);
Dyn1=AddLUTBearing(Dyn1,Num,1);
[Dyn1,Num]= AddCnode(Dyn1,310);
Dyn1=AddLUTBearing(Dyn1,Num,2);
Dyn1 = Dyn1.solve();
PlotCampbell(Dyn1,'NMode',9);
% PlotMode(Dyn1,1,1)
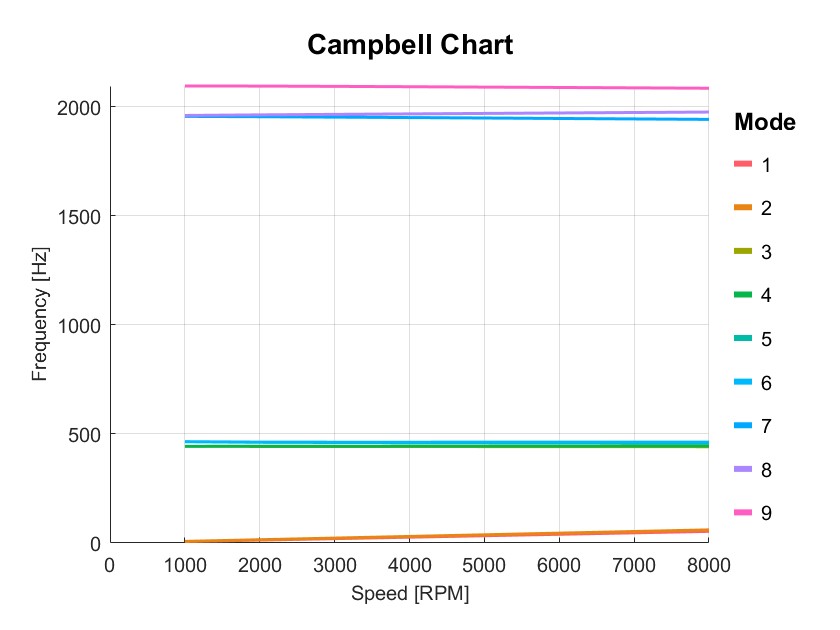
Disc rotor stationary analysis with PID controller (Flag=18)
对一个转子施加PID控制。
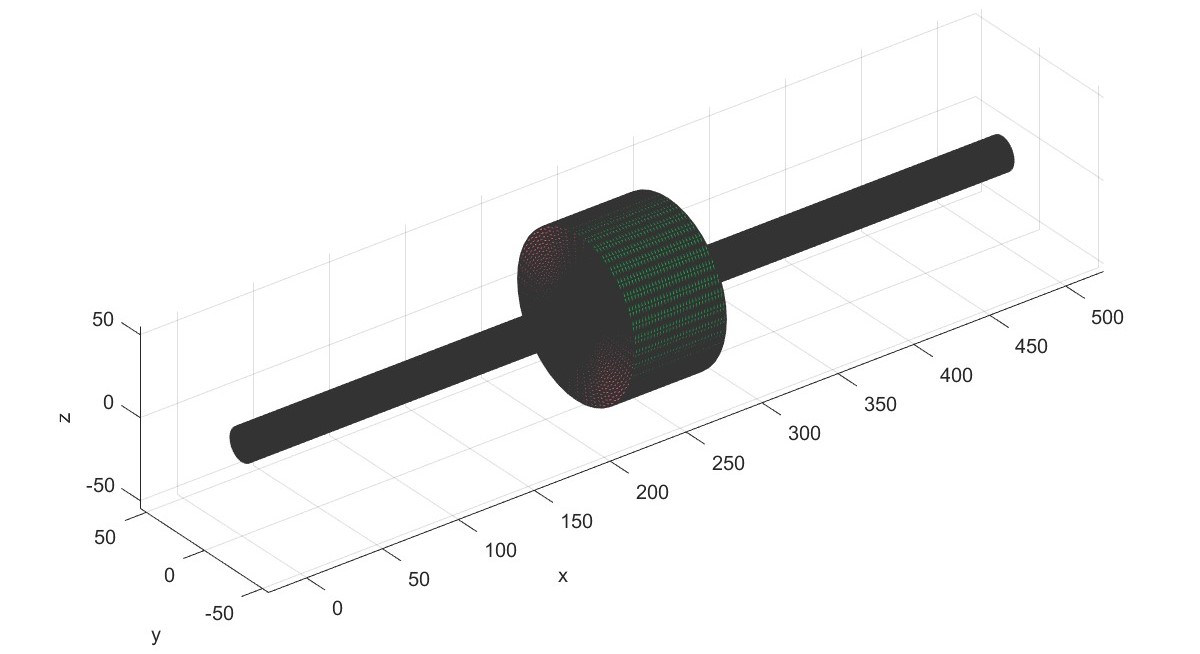
% Disc rotor
inputshaft1.Length = [220;280;500];
inputshaft1.ID = [[0,0];[0,0];[0,0]];
inputshaft1.OD = [[20,20];[100,100];[20,20]];
paramsshaft1.Beam_N = 16;
paramsshaft1.N_Slice=20;
Shaft = shaft.Commonshaft(paramsshaft1, inputshaft1);
Shaft = Shaft.solve();
Plot3D(Shaft)
% Load
inputLoad.Time=0:1e-4:0.5;
inputLoad.Fy=ones(1,length(inputLoad.Time));
paramsLoad=struct();
Load=signal.ForceLoad(paramsLoad, inputLoad);
Load=Load.solve();
Plot(Load);
mat{1,1}=Shaft.params.Material;
inputRotDyn.Shaft=Shaft.output.BeamMesh;
inputRotDyn.Speed=0;
inputRotDyn.MaterialNum=1;
paramsRotDyn.Material=mat;
paramsRotDyn.Type=4;
paramsRotDyn.Solver='Local';
paramsRotDyn.Rayleigh=[1e-5,10];
Dyn1 = solve.RotDyn(paramsRotDyn,inputRotDyn);
Dyn1 = AddBearing(Dyn1,1,[1e-3,1e3,1e3,0,0,0,0,0,0,0]);
[Dyn1,Num1]= AddCnode(Dyn1,500);
Dyn1 = AddBearing(Dyn1,Num1,[0,1e3,1e3,0,0,0,0,0,0,0]);
[Dyn1,Num2]= AddCnode(Dyn1,250);
Dyn1 = AddTimeSeries(Dyn1,Num2,Load.output.Load);
load pidTestLUT %#ok<LOAD>
% Dyn1 = AddPIDController(Dyn1,Num2,2e2/70,2e2/70,1/70,'Type',3,'Table',pidTestLUT,'Direction','Uy');
% Dyn1 = AddPIDController(Dyn1,Num2,2e2/70,2e2/70,1/70,'Type',3,'Table',pidTestLUT,'Direction','Uz');
Dyn1 = AddKeyNode(Dyn1,Num2);
Dyn1 = Dyn1.solve();
% PlotTimeSeriesResult(Dyn1,'Node',Dyn1.input.KeyNode,'Component',[1;2],'Load',1,'PIDController',1);
PlotTimeSeriesResult(Dyn1,'Node',Dyn1.input.KeyNode,'Component',[1;2],'Load',1);
无控制下转子中心位移。
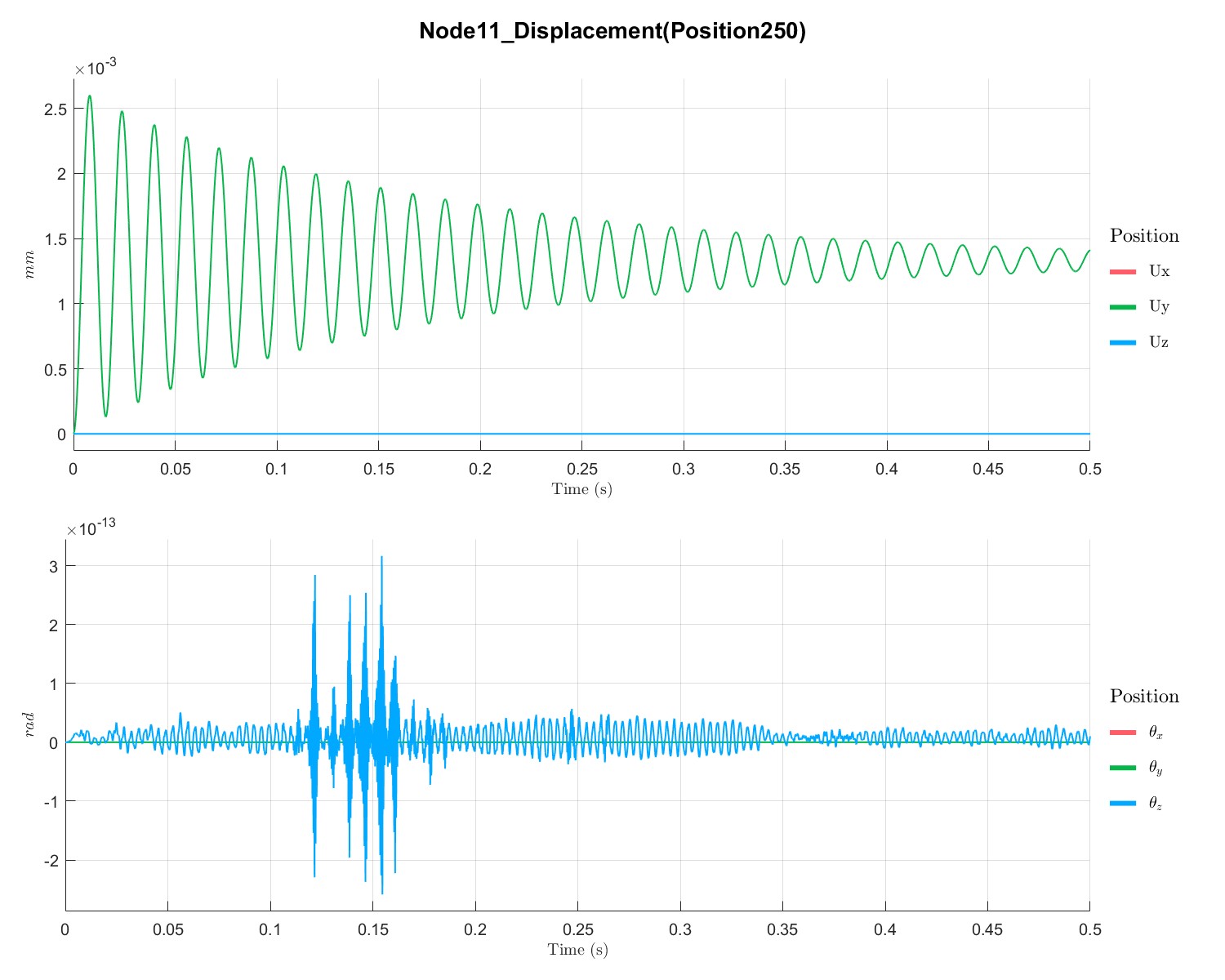
施加PID控制后,可以看到控制器给了转子一个反作用力,使得转子中心位移趋近于0mm.
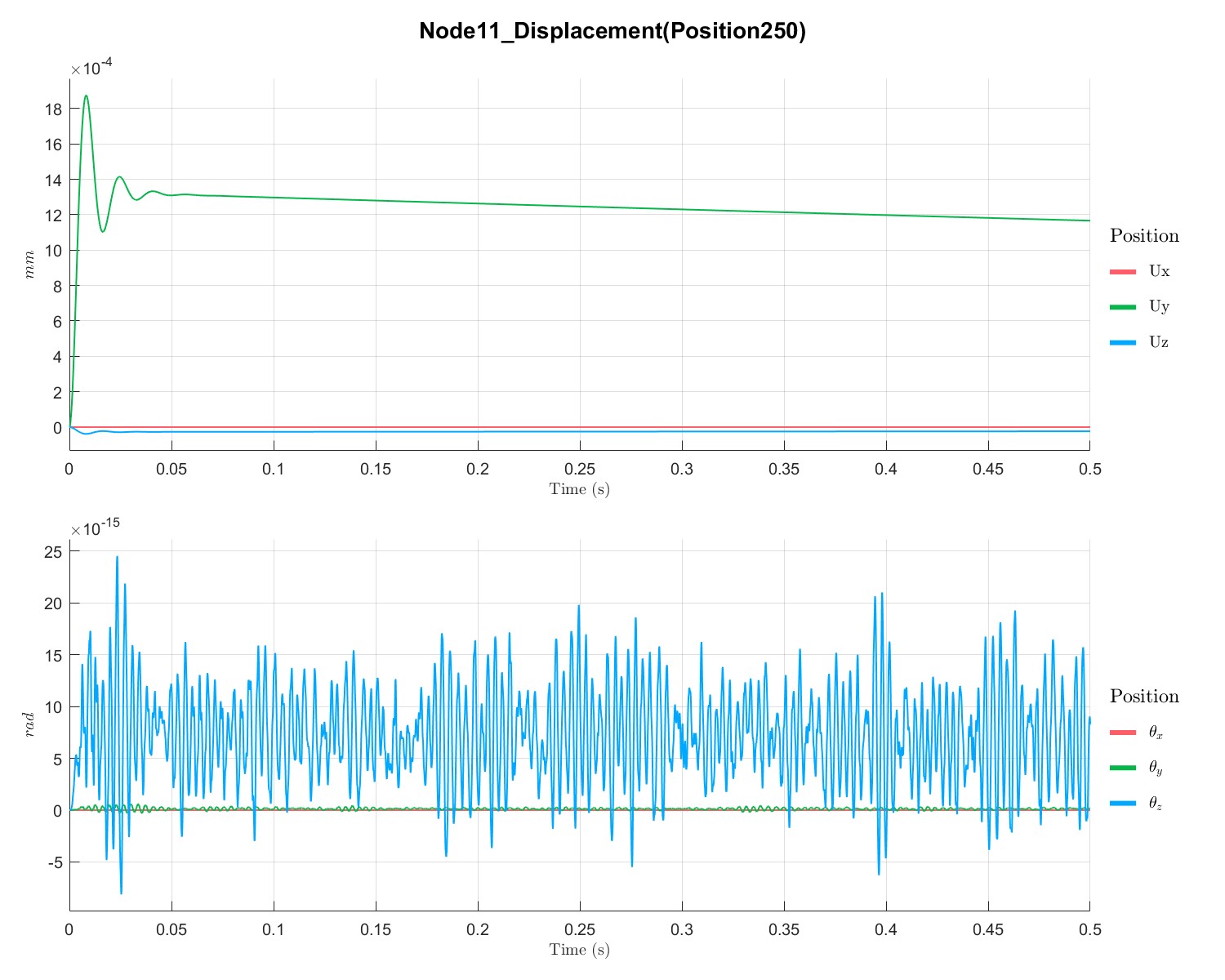
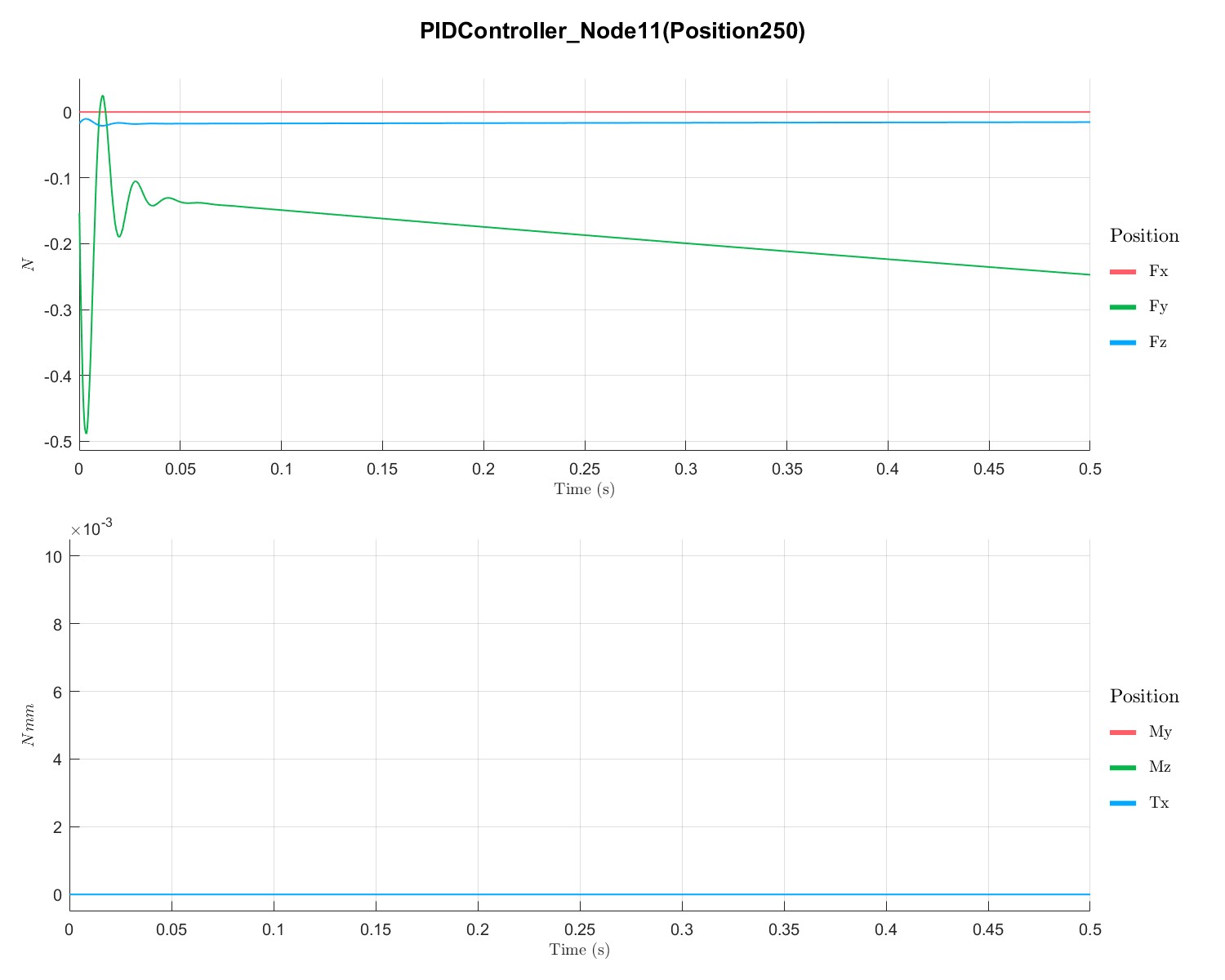
Disc rotor speedup analysis with PID controller (Flag=19)
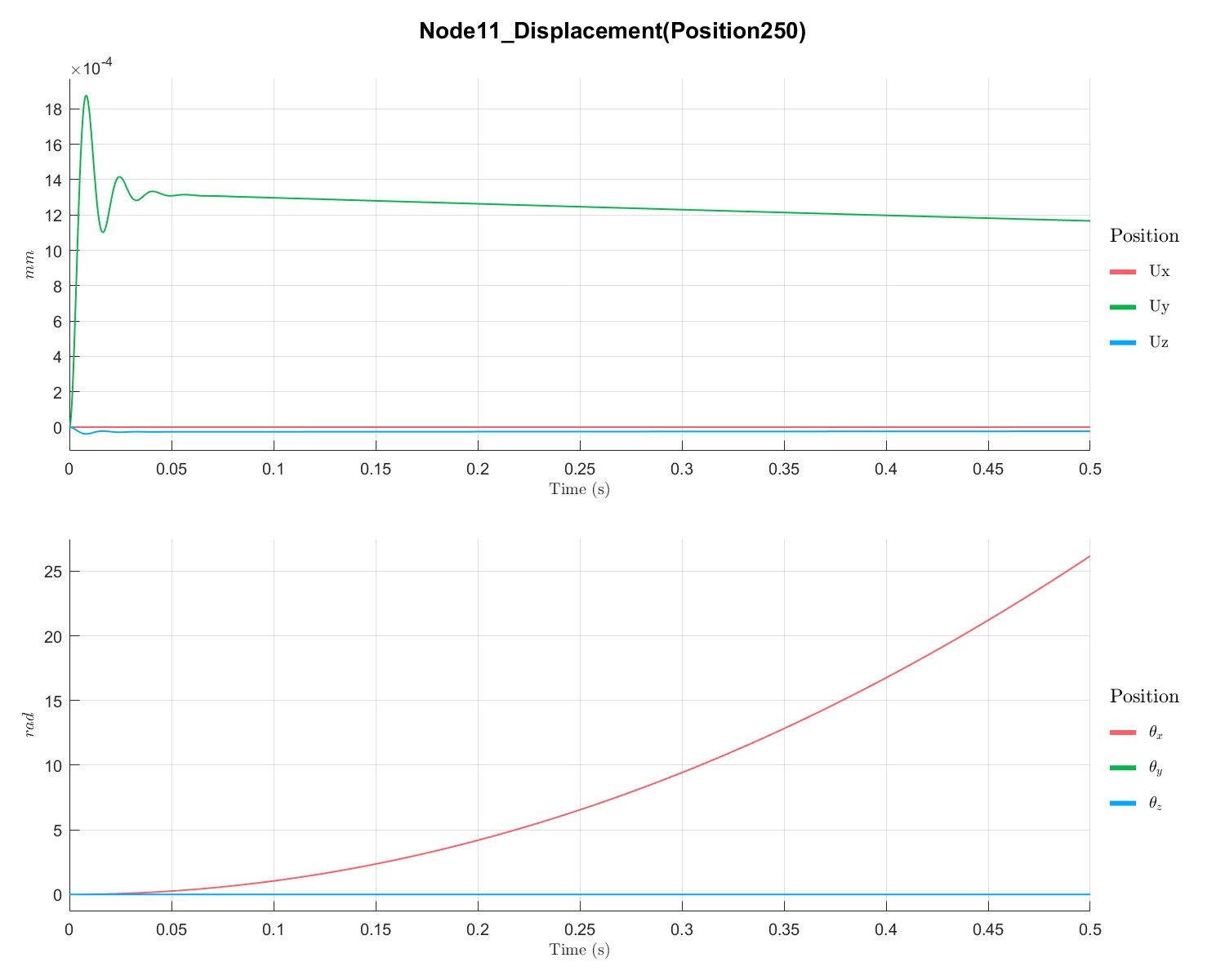
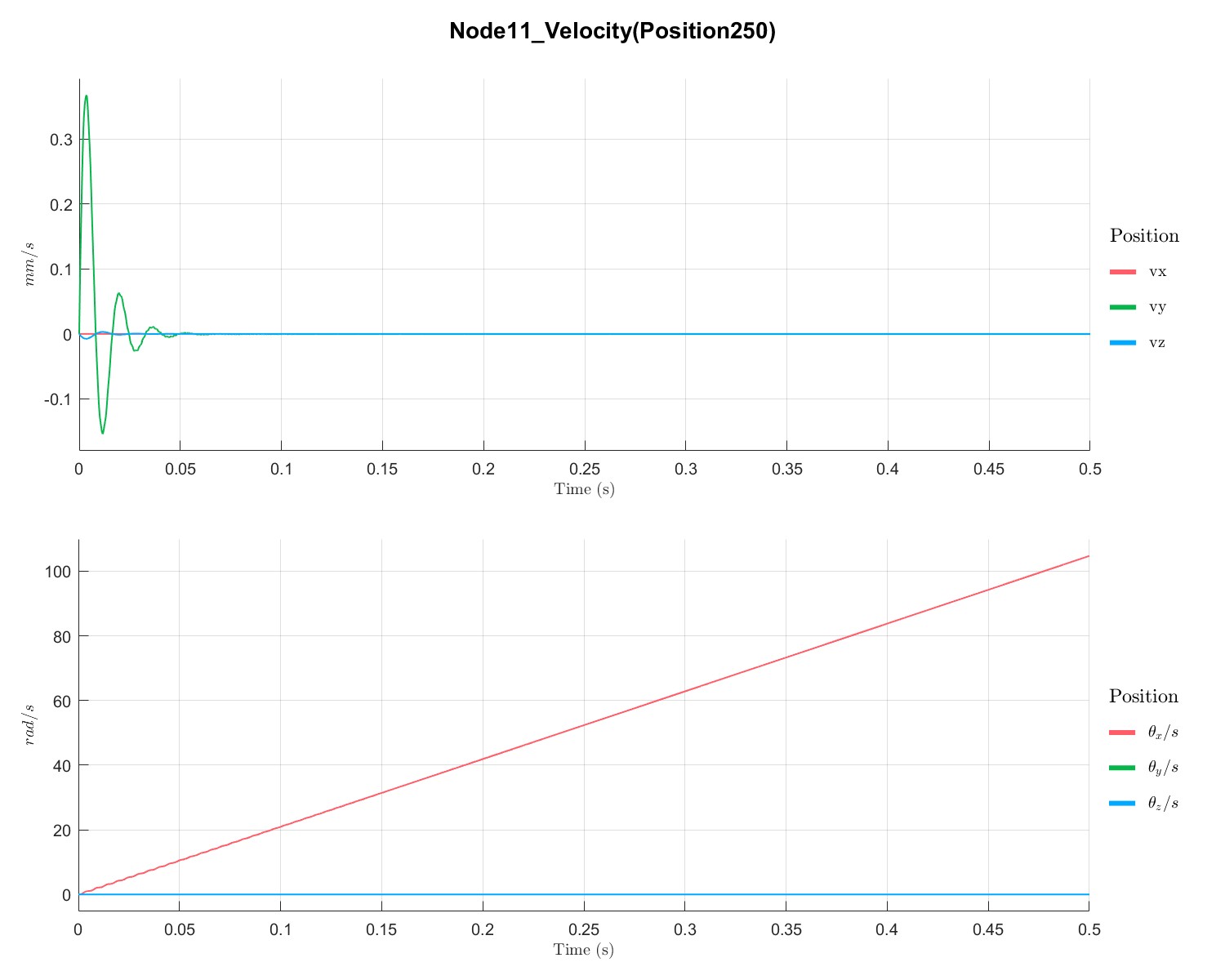
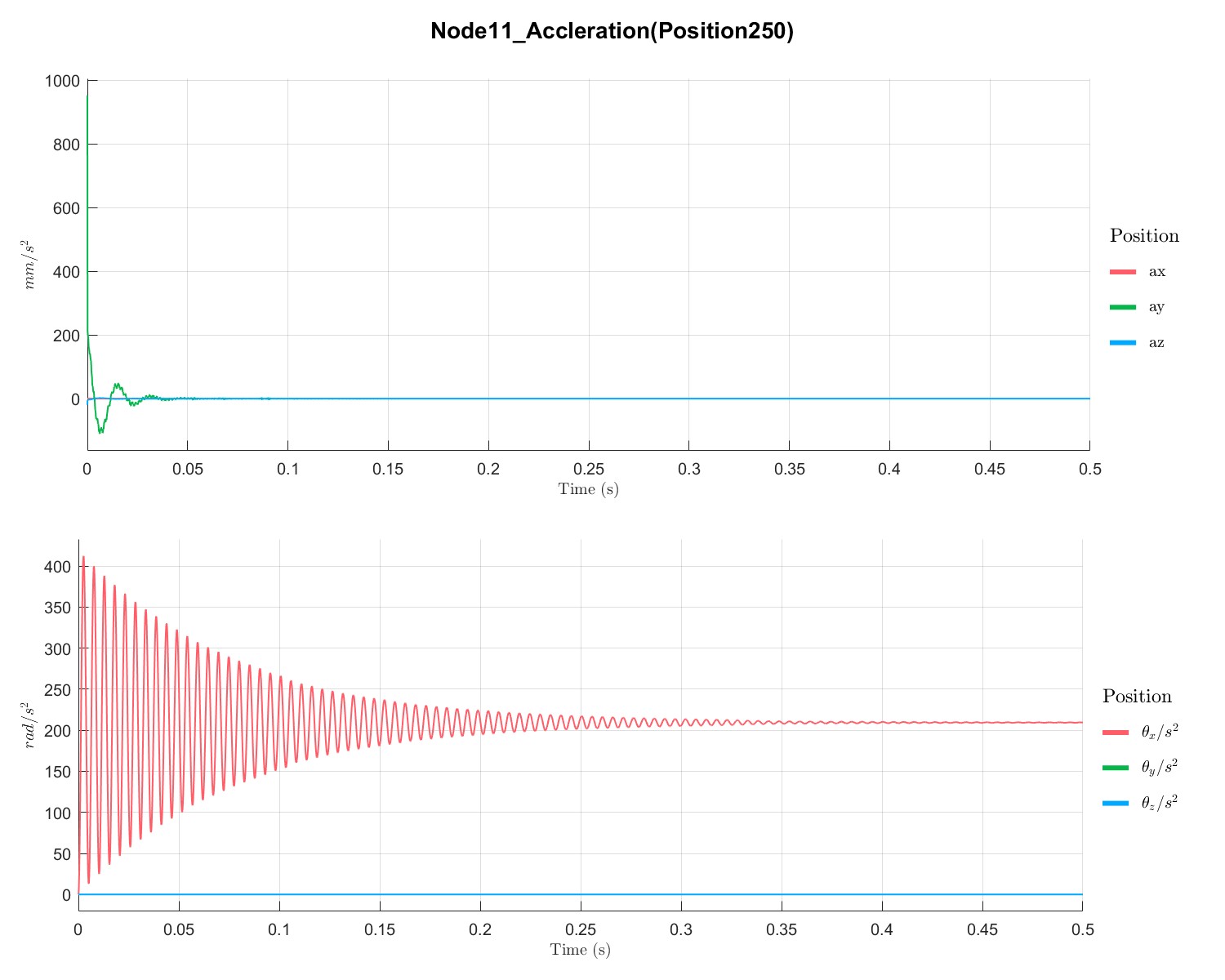
计算PID控制下转子的升速曲线
% Disc rotor
inputshaft1.Length = [220;280;500];
inputshaft1.ID = [[0,0];[0,0];[0,0]];
inputshaft1.OD = [[20,20];[100,100];[20,20]];
paramsshaft1.Beam_N = 16;
paramsshaft1.N_Slice=20;
Shaft = shaft.Commonshaft(paramsshaft1, inputshaft1);
Shaft = Shaft.solve();
Plot3D(Shaft)
% Load
inputLoad.Time=0:1e-4:0.5;
inputLoad.Fy=ones(1,length(inputLoad.Time));
paramsLoad=struct();
Load=signal.ForceLoad(paramsLoad, inputLoad);
Load=Load.solve();
Plot(Load);
mat{1,1}=Shaft.params.Material;
inputRotDyn.Shaft=Shaft.output.BeamMesh;
inputRotDyn.SpeedRange=[0,1000];
inputRotDyn.MaterialNum=1;
paramsRotDyn.Material=mat;
paramsRotDyn.Type=5;
paramsRotDyn.Solver='Local';
paramsRotDyn.Rayleigh=[1e-5,10];
Dyn1 = solve.RotDyn(paramsRotDyn,inputRotDyn);
Dyn1 = AddBearing(Dyn1,1,[1e-3,1e3,1e3,0,0,0,0,0,0,0]);
[Dyn1,Num1]= AddCnode(Dyn1,500);
Dyn1 = AddBearing(Dyn1,Num1,[0,1e3,1e3,0,0,0,0,0,0,0]);
[Dyn1,Num2]= AddCnode(Dyn1,250);
Dyn1 = AddTimeSeries(Dyn1,Num2,Load.output.Load);
load pidTestLUT %#ok<LOAD>
Dyn1 = AddPIDController(Dyn1,Num2,2e2/70,2e2/70,1/70,'Type',3,'Table',pidTestLUT,'Direction','Uy');
Dyn1 = AddPIDController(Dyn1,Num2,2e2/70,2e2/70,1/70,'Type',3,'Table',pidTestLUT,'Direction','Uz');
Dyn1 = AddKeyNode(Dyn1,Num2);
Dyn1 = Dyn1.solve();
PlotTimeSeriesResult(Dyn1,'Node',Dyn1.input.KeyNode,'Component',[1;2],'Load',1,'PIDController',1);
Rotor speedup analysis with AMB (Flag=20)
带主动磁力轴承的转子动力学分析。
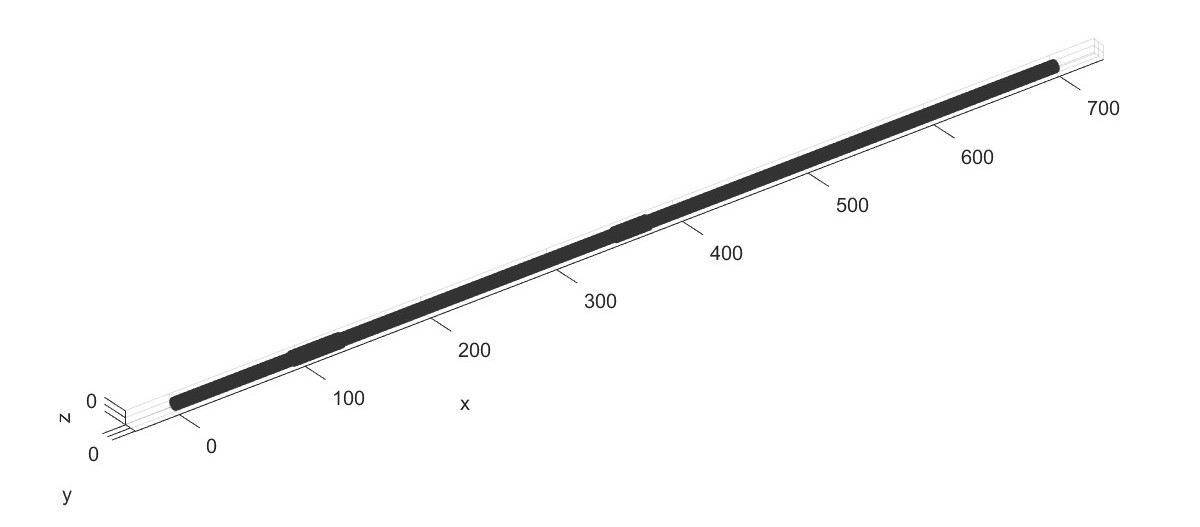
% Shaft
inputshaft1.Length = [94;132;350;376;700];
inputshaft1.ID = [[0,0];[0,0];[0,0];[0,0];[0,0]];
inputshaft1.OD = [[8,8];[9.6,9.6];[8,8];[9.6,9.6];[8,8]];
paramsshaft1.Beam_N = 16;
paramsshaft1.N_Slice=50;
Shaft = shaft.Commonshaft(paramsshaft1, inputshaft1);
Shaft = Shaft.solve();
Plot3D(Shaft)
% Load
inputStruct2.Time=0:1e-3:0.2;
inputStruct2.Fy=rand(1,length(inputStruct2.Time));
paramsStruct2=struct();
Load1=signal.ForceLoad(paramsStruct2, inputStruct2);
Load1=Load1.solve();
Plot(Load1);
Load2=signal.ForceLoad(paramsStruct2, inputStruct2);
Load2=Load2.solve();
Plot(Load2);
mat{1,1}=Shaft.params.Material;
inputRotDyn.Shaft=Shaft.output.BeamMesh;
inputRotDyn.SpeedRange=[0,1000];
inputRotDyn.MaterialNum=1;
paramsRotDyn.Material=mat;
paramsRotDyn.Type=5;
paramsRotDyn.Solver='Local';
paramsRotDyn.Rayleigh=[1e-5,10];
% Add disc
Dyn1 = solve.RotDyn(paramsRotDyn,inputRotDyn);
[Dyn1,Num1]= AddCnode(Dyn1,113);
Dyn1=AddPointMass(Dyn1,Num1,0.85074e-3,4.036839e-1,4.840066e-1);
[Dyn1,Num2]= AddCnode(Dyn1,363);
Dyn1=AddPointMass(Dyn1,Num2,1.276499e-3,2.83275,1.487212);
[Dyn1,Num3]= AddCnode(Dyn1,623);
Dyn1=AddPointMass(Dyn1,Num3,0.8574e-3,4.036839e-1,4.840066e-1);
% Add Bearing
Dyn1 = AddBearing(Dyn1,Num1,[1e7,1e7,1e7,0,0,0,0,0,0,0]);
Dyn1 = AddBearing(Dyn1,Num1,[0,-1e2,-1e2,0,0,0,0,0,0,0]);
Dyn1 = AddBearing(Dyn1,Num3,[0,-1e2,-1e2,0,0,0,0,0,0,0]);
% Add PIDController
Dyn1 = AddPIDController(Dyn1,Num1,5,1.5,5e-3,'Type',1,'Ki',50,'Direction','Uy');
Dyn1 = AddPIDController(Dyn1,Num1,5,1.5,5e-3,'Type',1,'Ki',50,'Direction','Uz');
Dyn1 = AddPIDController(Dyn1,Num3,5,1.5,5e-3,'Type',1,'Ki',50,'Direction','Uy');
Dyn1 = AddPIDController(Dyn1,Num3,5,1.5,5e-3,'Type',1,'Ki',50,'Direction','Uz');
% Add Timeseries
Dyn1 = AddTimeSeries(Dyn1,Num1,Load1.output.Load);
Dyn1 = AddTimeSeries(Dyn1,Num3,Load2.output.Load);
Dyn1 = Dyn1.solve();
PlotTimeSeriesResult(Dyn1,'Node',Dyn1.input.KeyNode,'Component',[1;2;3],'Load',[1;2],'PIDController',[1;3]);
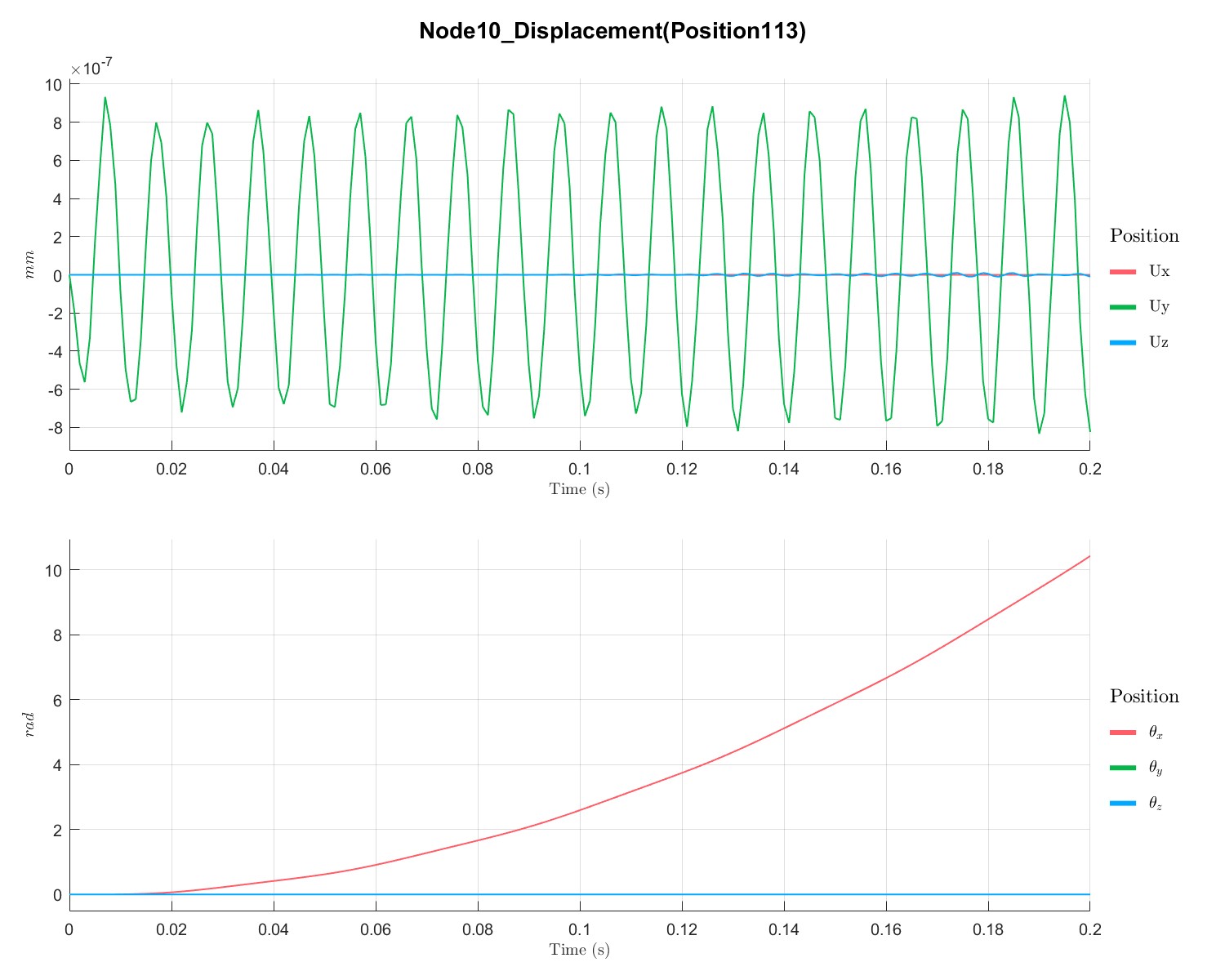


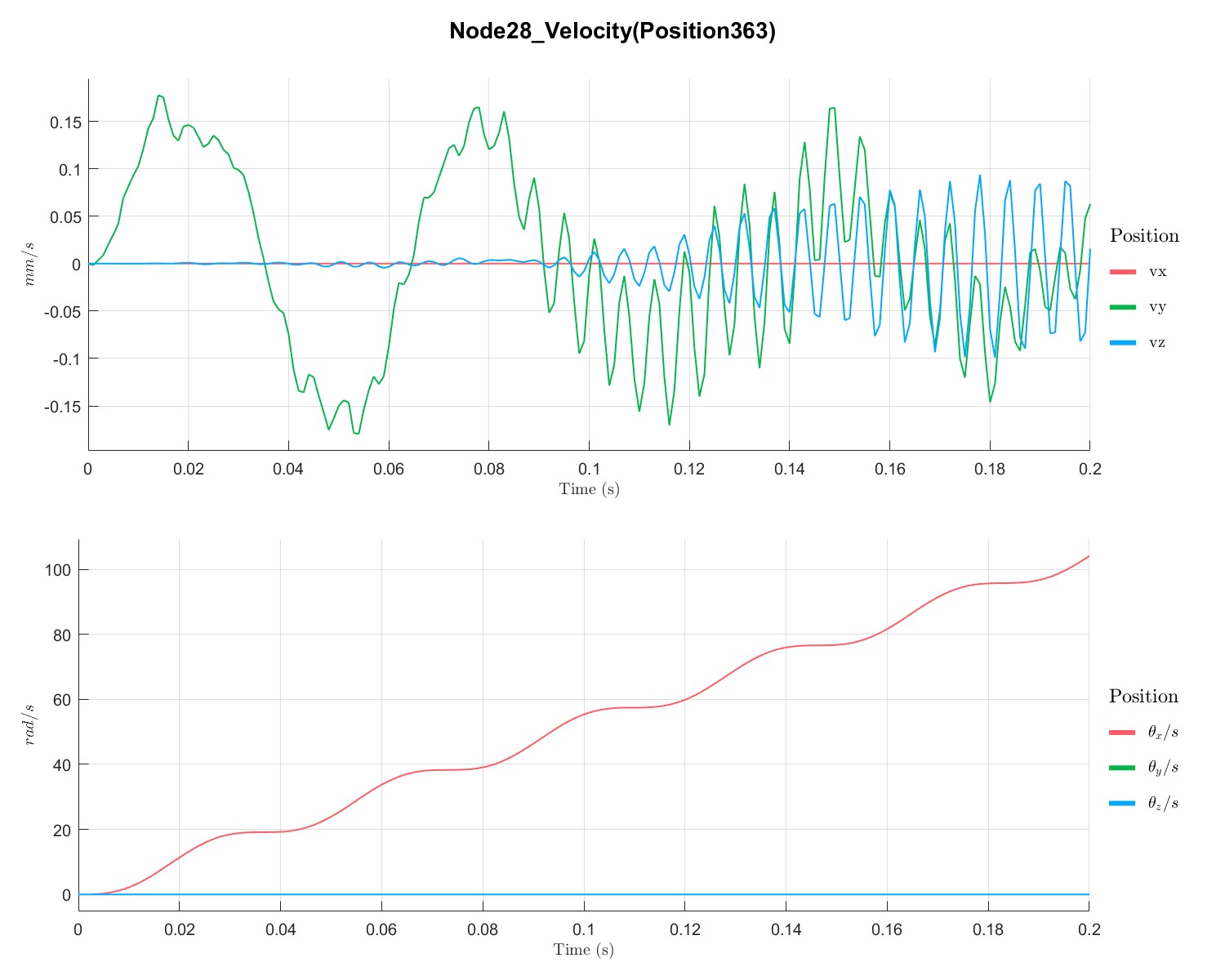
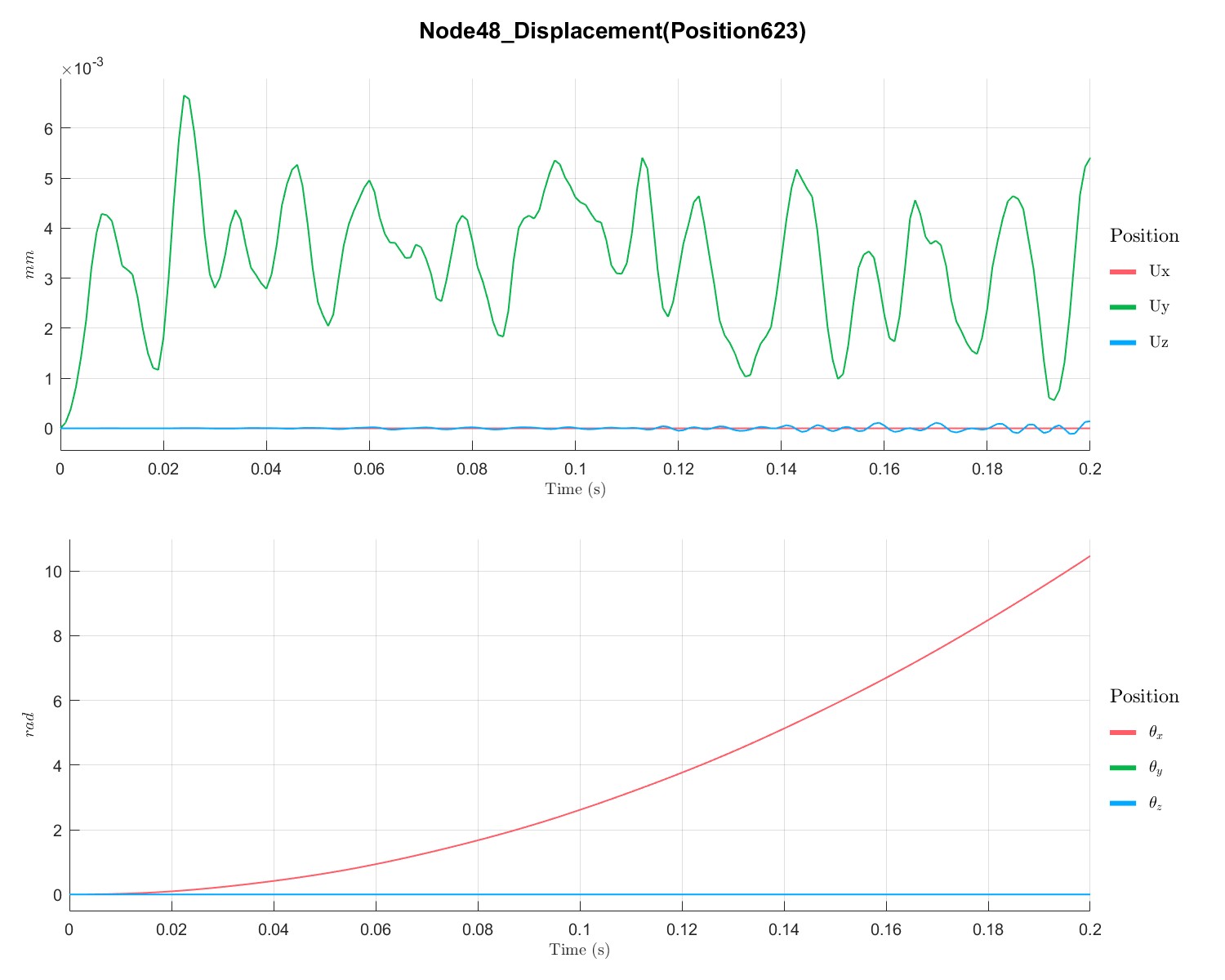
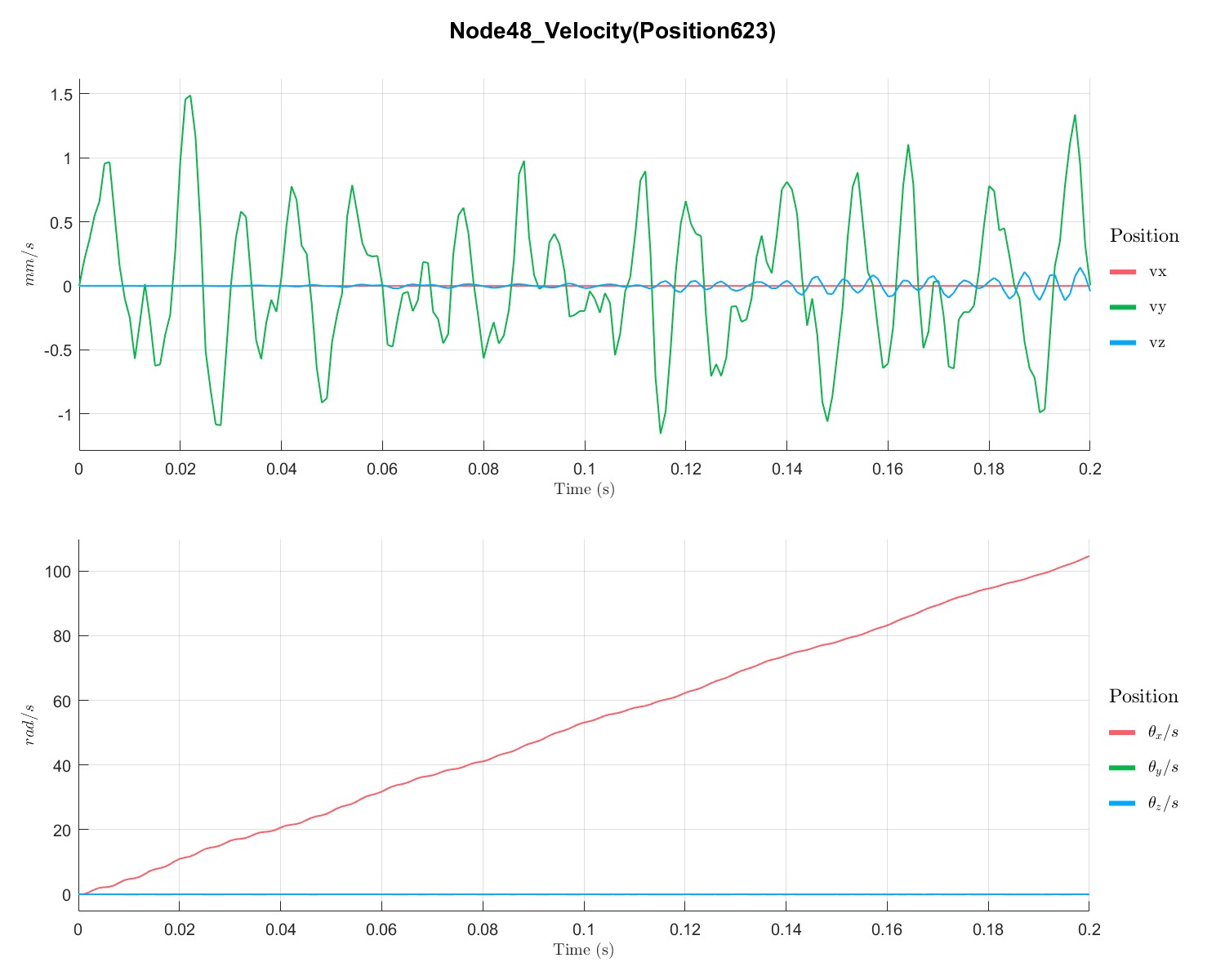
Generate unbalance time series (Flag=21)
当设置不平衡的载荷时,RotDyn会根据不平衡量生成不平衡载荷时序。
% Shaft
inputshaft1.Length = [35;45;70;200;250;300];
inputshaft1.ID = [[0,0];[10,10];[10,10];[10,10];[10,10];[10,10]];
inputshaft1.OD = [[40,40];[70,70];[40,40];[40,40];[40,40];[70,70]];
paramsshaft1.Beam_N = 16;
paramsshaft1.N_Slice=201;
obj1 = shaft.Commonshaft(paramsshaft1, inputshaft1);
obj1 = obj1.solve();
Plot3D(obj1)
mat{1,1}=obj1.params.Material;
inputRotDyn.Shaft=obj1.output.BeamMesh;
inputRotDyn.Speed=1000;
inputRotDyn.SpeedRange=[0,1000];
inputRotDyn.PointMass=[1,1.2e-3,2.4,1.2;size(obj1.output.Node,1),1e-3,2,1];
inputRotDyn.MaterialNum=1;
inputRotDyn.Time=0:1e-4:1;
inputRotDyn.BalanceQuality=[2.5,3000,0,300,0];
paramsRotDyn.Material=mat;
paramsRotDyn.Rayleigh=[1e-5,10];
paramsRotDyn.Type=4;
%paramsRotDyn.Type=5;
Dyn1 = solve.RotDyn(paramsRotDyn,inputRotDyn);
[Dyn1,Num1]= AddCnode(Dyn1,70);
Dyn1=AddBearing(Dyn1,Num1,[1e10,8e4,1e5,1e4,6e4,0,8,12,3,3]);
[Dyn1,Num2]= AddCnode(Dyn1,200);
Dyn1=AddBearing(Dyn1,Num2,[0,5e4,7e4,2e4,4e4,0,6,8,1.5,1.5]);
Dyn1 = Dyn1.solve();
PlotTimeSeriesResult(Dyn1,'Node',Dyn1.input.KeyNode,'Component',[1;2]);
在 1000 rpm下,转子的响应:
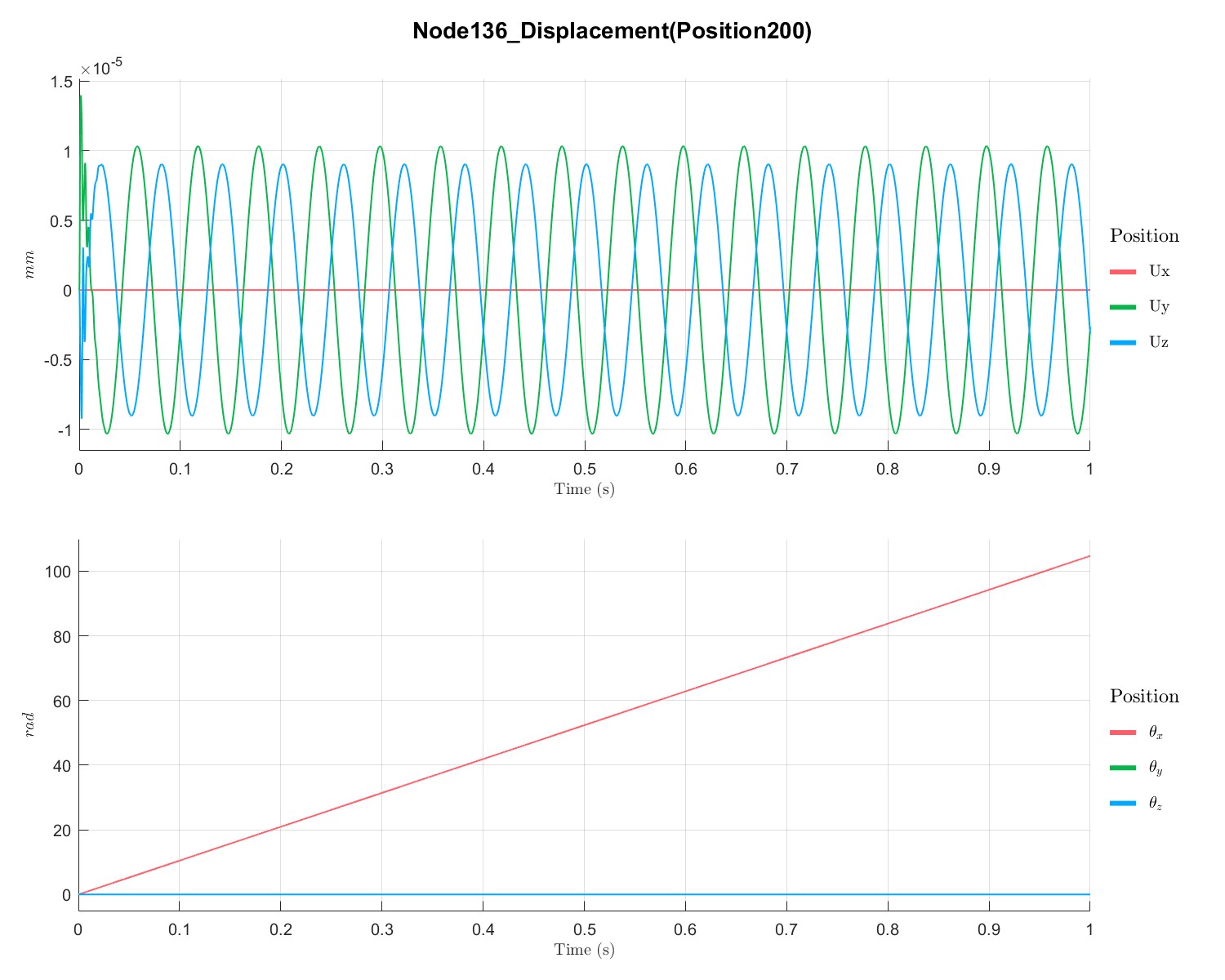
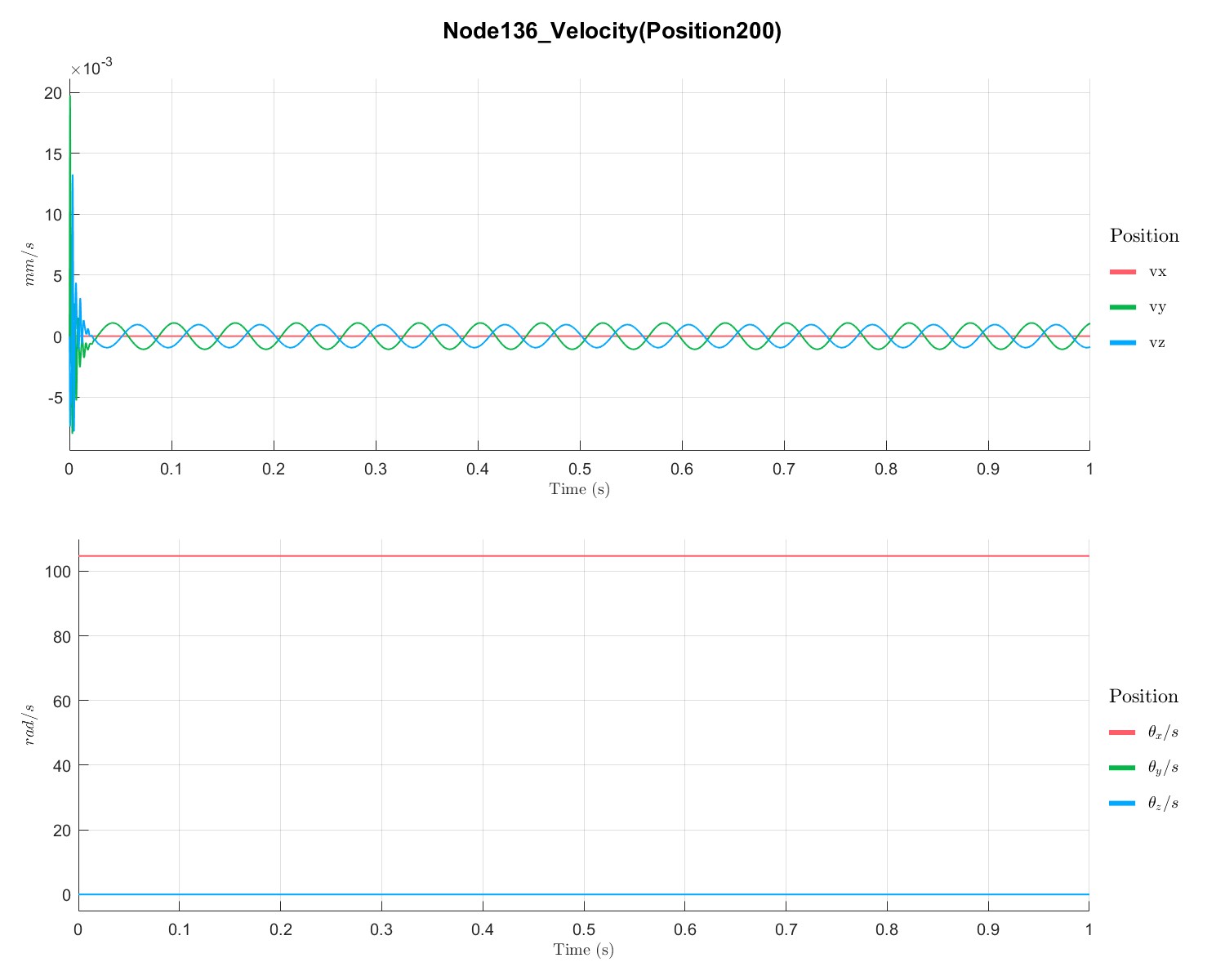
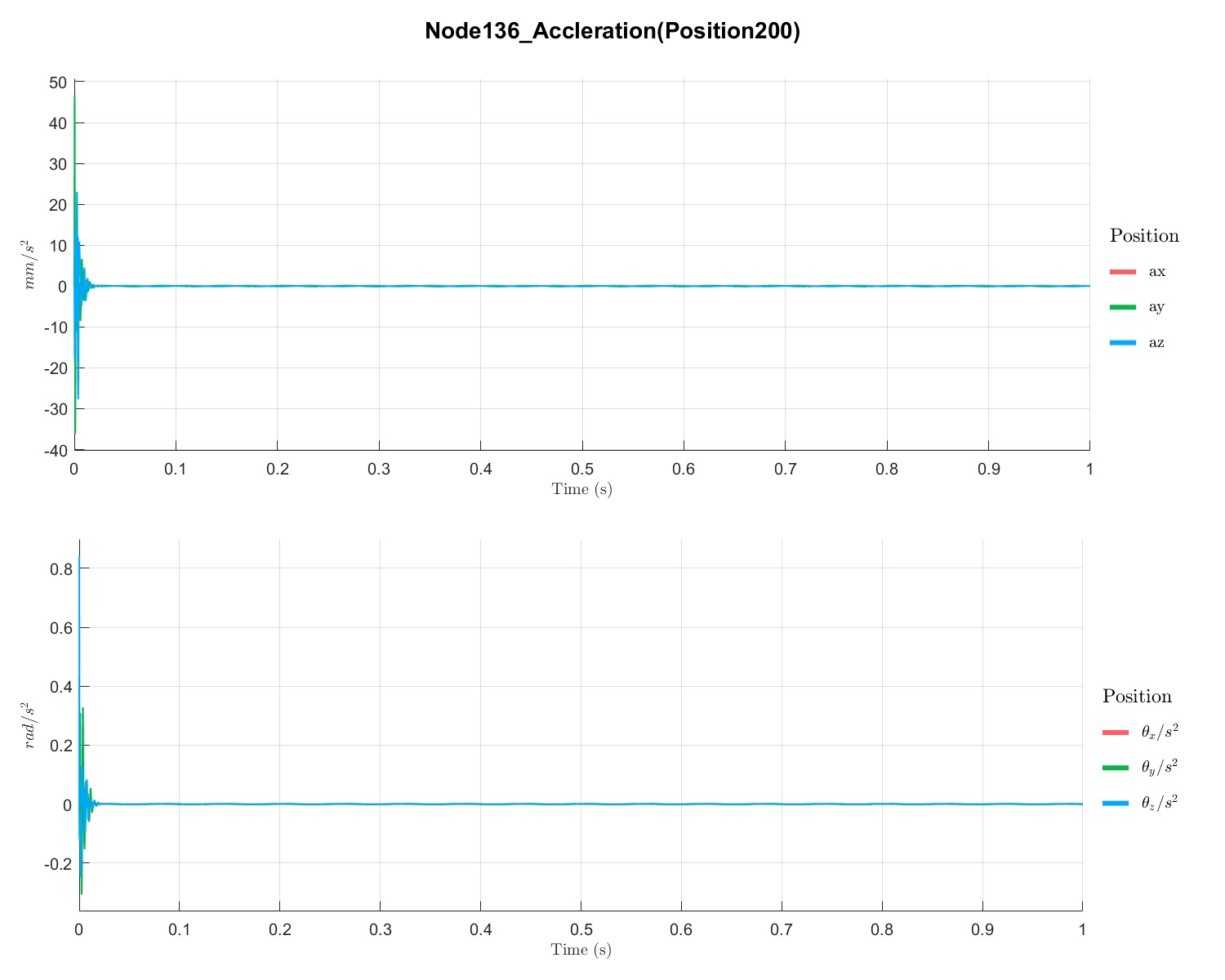
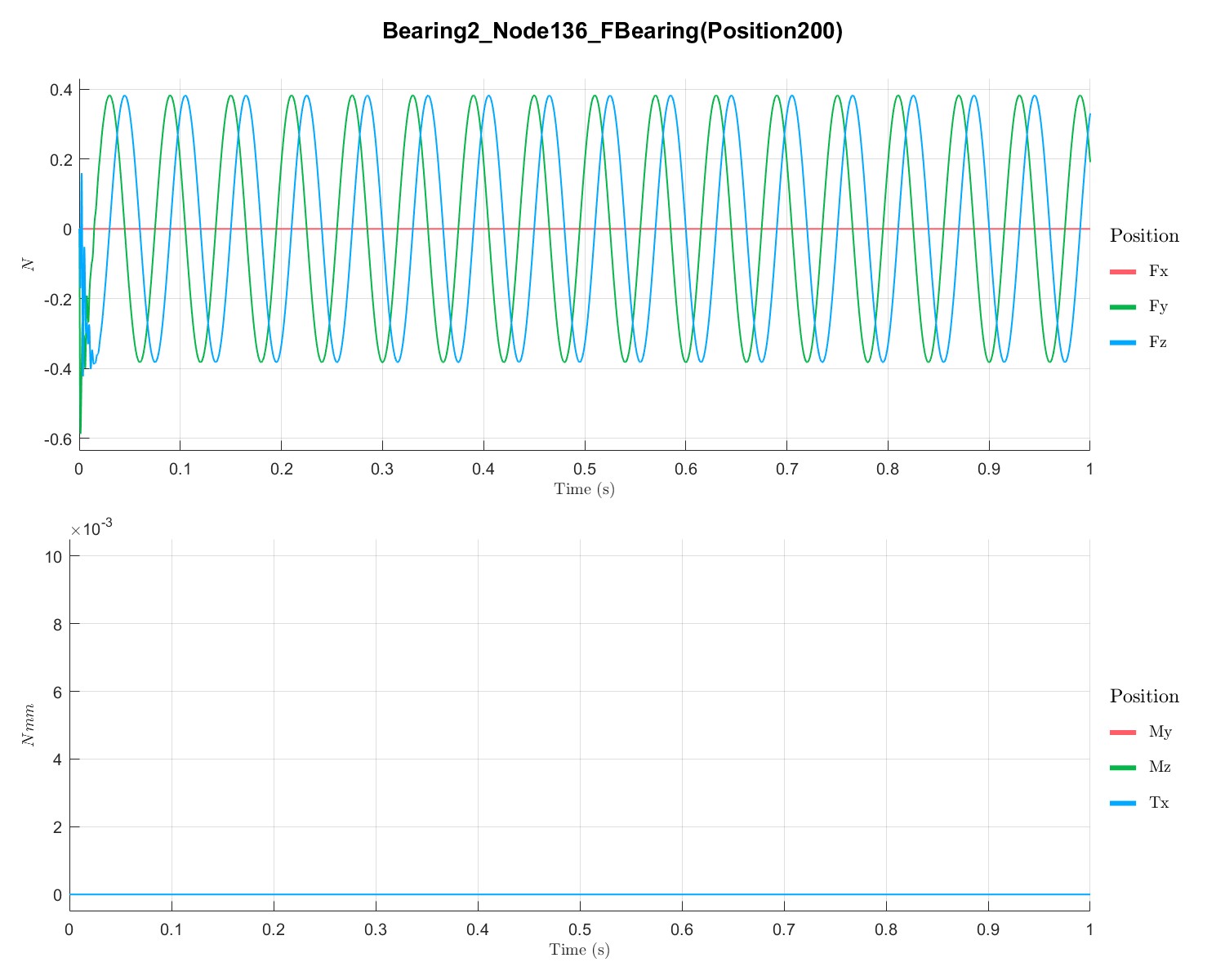
1s内由0 RPM升速到 1000 RPM 下转子的响应:
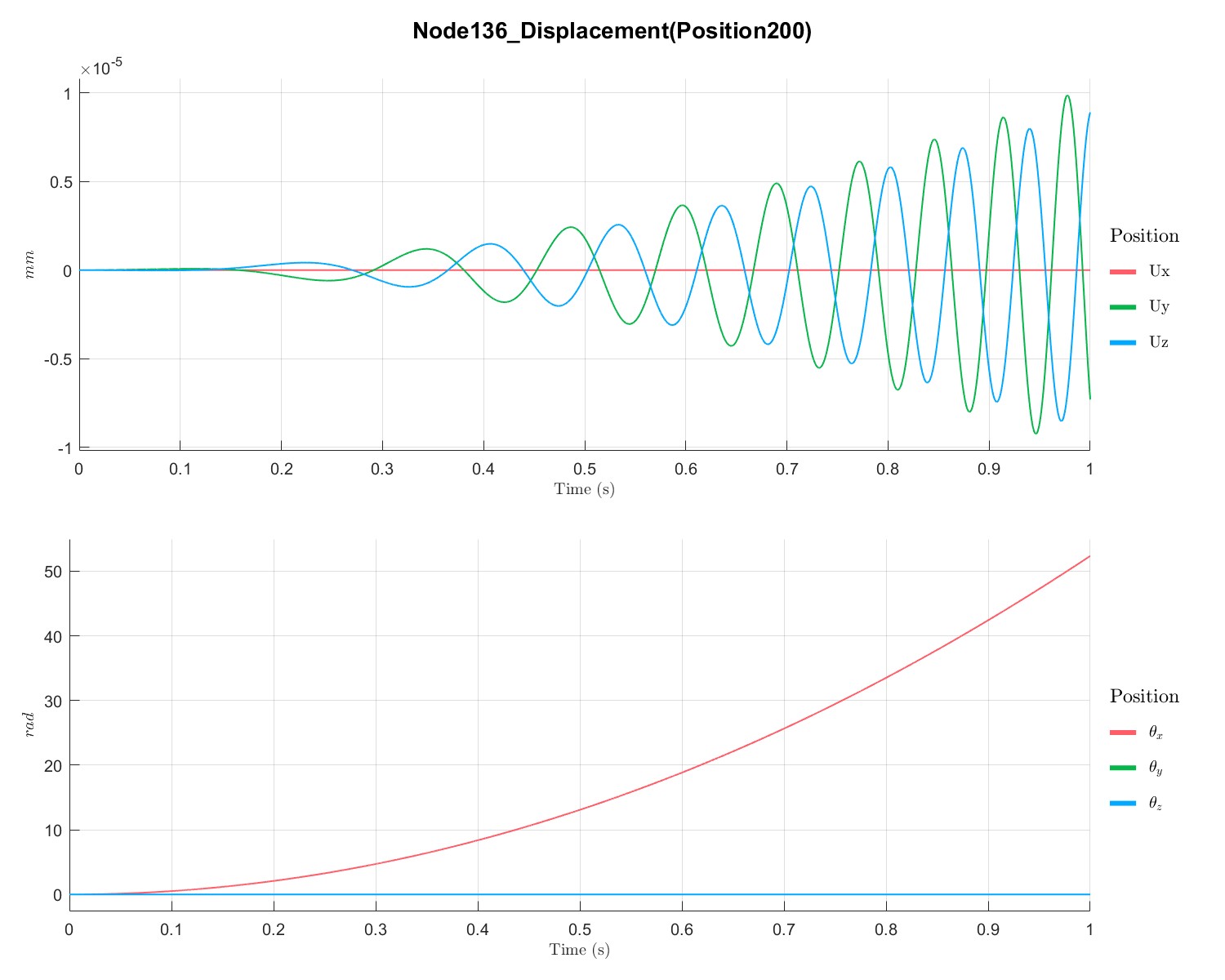
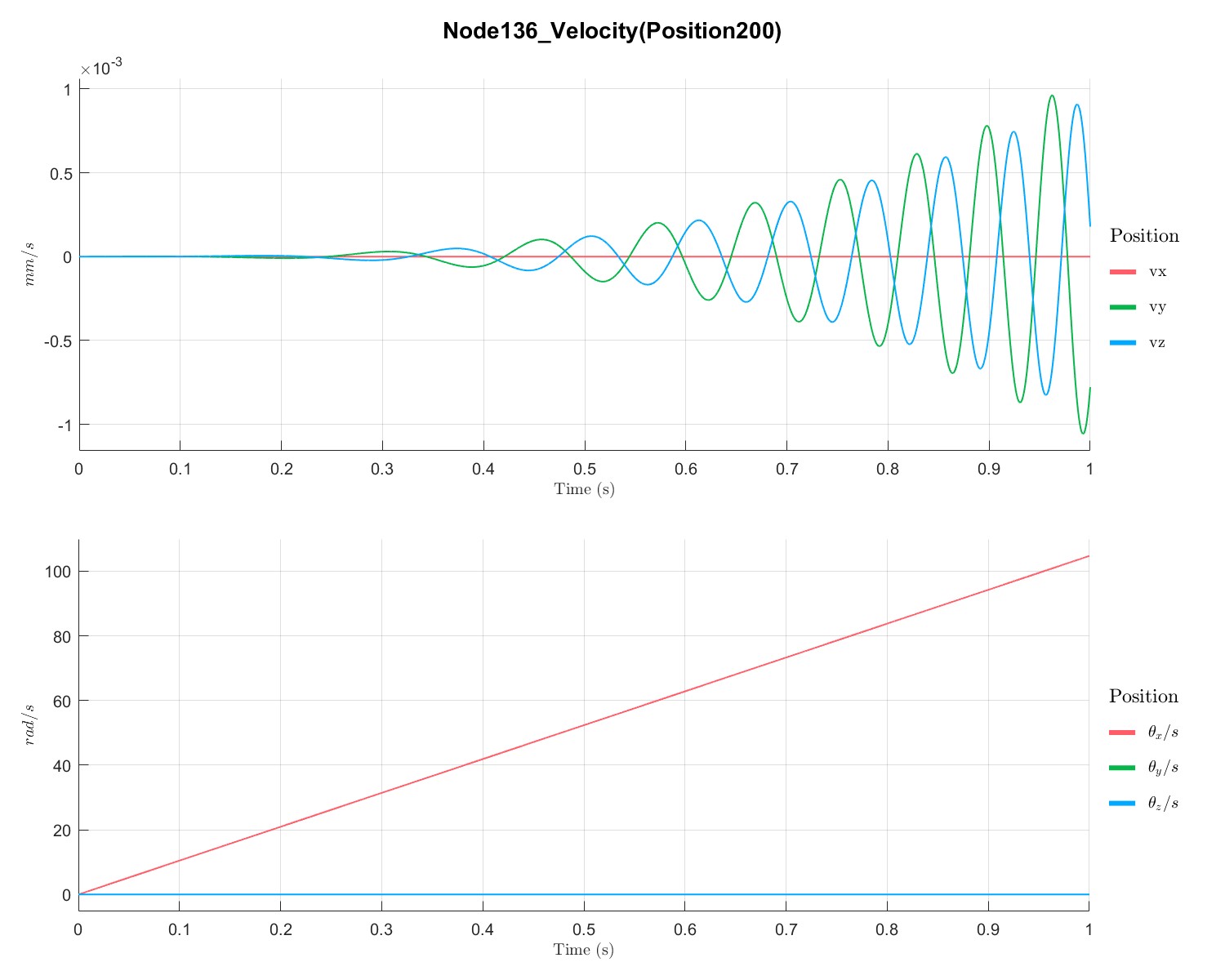
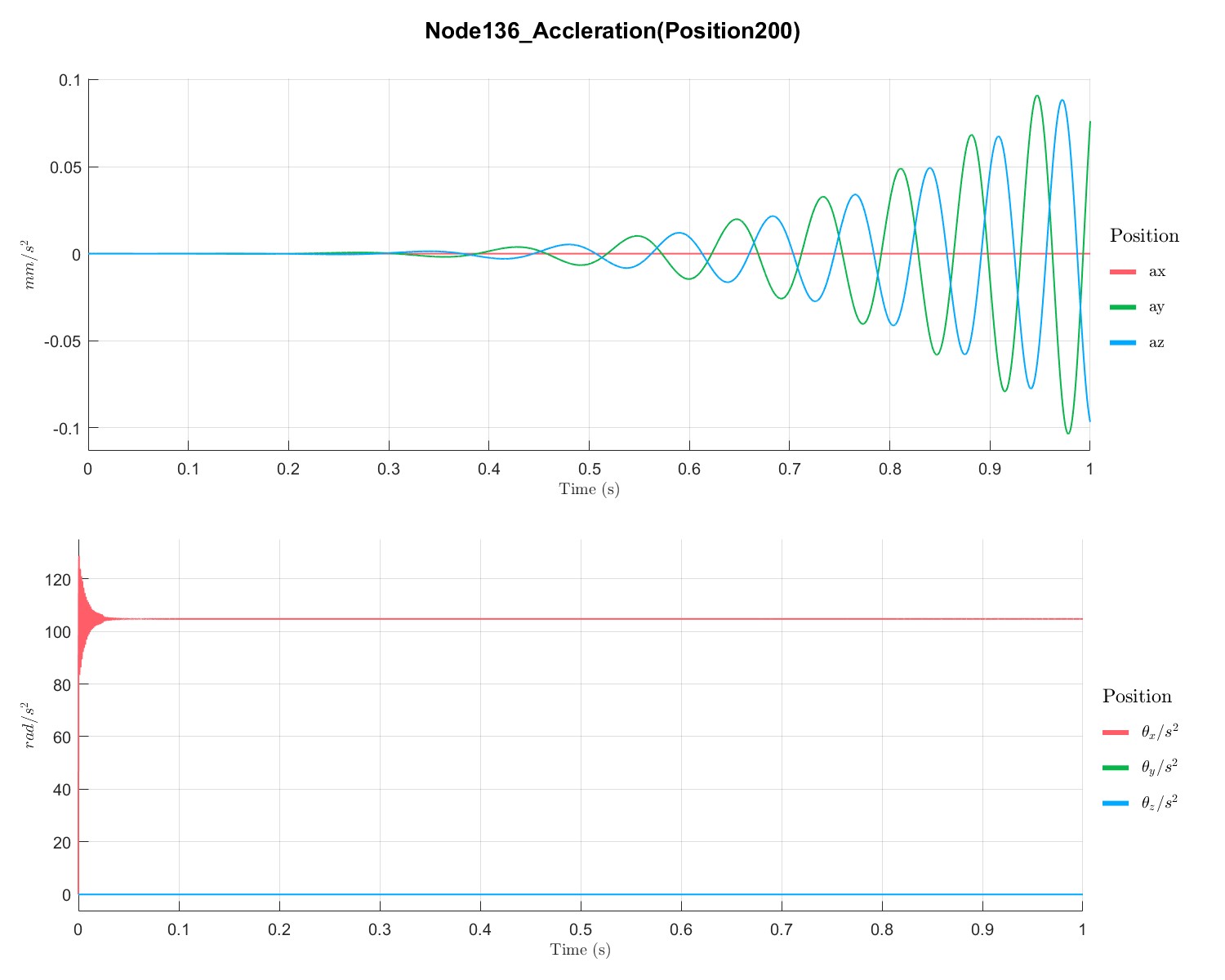

参考文献
[1] ANSYS结构动力分析与应用
[2] 转动机械的转子动力学设计
[3] https://github.com/AppliedMechanics/AMrotor
[4] AMrotor – A MATLAB Toolbox for the Simulation of Rotating Machinery, Johannes Maierhofer, M.Kreutz, T.Mulser, T. Thümmel, D. Rixen. DOI: 10.1201/9781003132639
[5] Comparison of different time integration schemes and application to a rotor system with magnetic bearings in Matlab, Michael Kreutz, J. Maierhofer, T. Thümmel, D. Rixen. DOI: 10.1201/9781003132639
本网站基于Hexo 3-Hexz主题生成。如需转载请标注来源,如有错误请批评指正,欢迎邮件至 392176462@qq.com