RayleighEstimate

Line2D

介绍

Line2D类是用来生成2D的曲线，主要参考了FEM19$^{[1][2][3][4]}$开源项目。

关键曲线的参数：

CT： 曲线类型（1：直线 2：圆弧 3：曲线 4：椭圆弧 5：贝塞尔6：B样条7：样条8：抛物线9：双曲线10：Nurb曲线）

CIX： 曲线编号

C ： 曲线数据

案例

Add different curves (Flag=1)

%% AddLine
x1=[-1;1];
y1=[-3;-3];
a=Point2D('Point Ass1');
a=AddPoint(a,x1,y1);
b=Line2D('Line Ass1');
b=AddLine(b,a,1);
Plot(b,'clabel',1,'styles',{'-'});
%% AddCurve
x2=[0;0.3;-0.3;0];
y2=[0;-1;-1;0];
a=AddPoint(a,x2,y2);
b=AddCurve(b,a,2);
Plot(b,'clabel',1,'styles',{'-'},'equal',0);
%% AddCircle
x3=-3;y3=2;
x4=3;y4=2;
x5=0;y5=0;
a=AddPoint(a,x3,y3);
a=AddPoint(a,x4,y4);
a=AddPoint(a,x5,y5);
b=AddCircle(b,0.5,a,3);
b=AddCircle(b,0.5,a,4);
b=AddCircle(b,5,a,5);
Plot(b,'clabel',1,'styles',{'-'},'equal',1);
%% AddEllipse
x6=0;y6=-3;
a=AddPoint(a,x6,y6);
b=AddEllipse(b,1,0.5,a,6,'rot',-90,'sang',-90,'ang',180);
Plot(b,'clabel',1,'styles',{'-'},'equal',1);
%% AddSpline
x7=[-4;-3;-2];y7=[2.5;3;2.5];
a=AddPoint(a,x7,y7);
b=AddSpline(b,1,a,7);
Plot(b,'clabel',1,'styles',{'-'},'equal',1);
%% AddBezier
x8=[4;3;2];y8=[2.5;3;2.5];
a=AddPoint(a,x8,y8);
b=AddBezier(b,a,8);
Plot(b,'clabel',1,'styles',{'-'},'equal',1);
%% AddBspline
x9=[-1.5;0;1.5];y9=[3;3.5;3];
a=AddPoint(a,x9,y9);
b=AddBspline(b,3,a,9);
Plot(b,'clabel',1,'styles',{'-'},'equal',1);
%% AddHyperbola
b1=Line2D('Line Ass2');
b1=AddHyperbola(b1, 2, 1,a,5,'t1',-1,'t2',3);
b1=AddHyperbola(b1, 1, 1,a,5,'t1',-3,'t2',3);
b1=AddHyperbola(b1, 2, 1,a,5,'rot',90,'t1',-3,'t2',3);
Plot(b1,'clabel',1,'styles',{'--'},'equal',1);
%% AddParabola
b2=Line2D('Line Ass3');
b2=AddParabola(b2, 2,a,5,'t1',-1,'t2',3);
b2=AddParabola(b2, 1,a,5,'t1',-3,'t2',3);
b2=AddParabola(b2, 2,a,5,'rot',90,'t1',-3,'t2',3);
Plot(b2,'clabel',1,'styles',{':'},'equal',1);

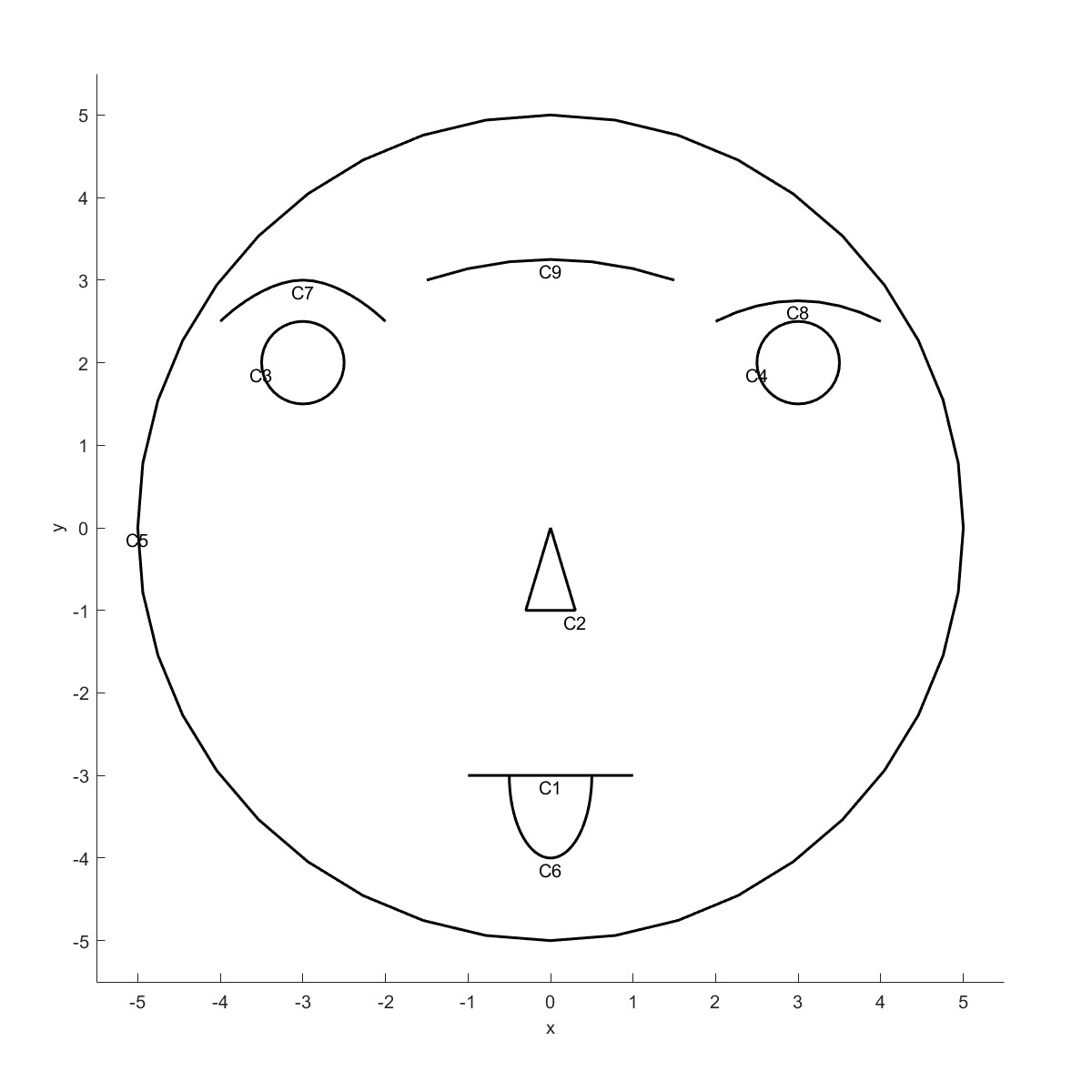
C1为直线，C2为多段的曲线，C3~C5为圆形，C6为半圆弧，C7为样条曲线，C8为贝塞尔曲线，C9为B样条

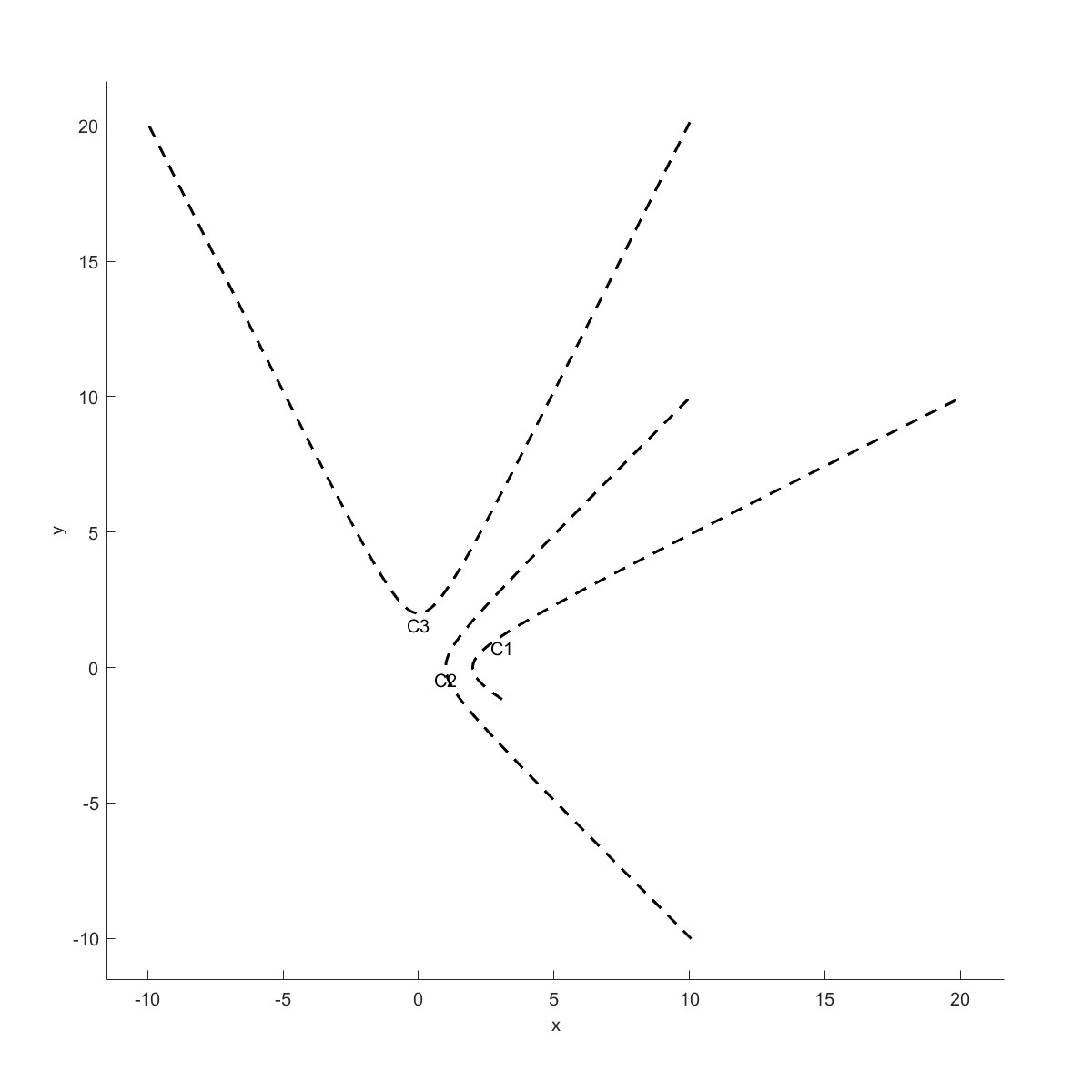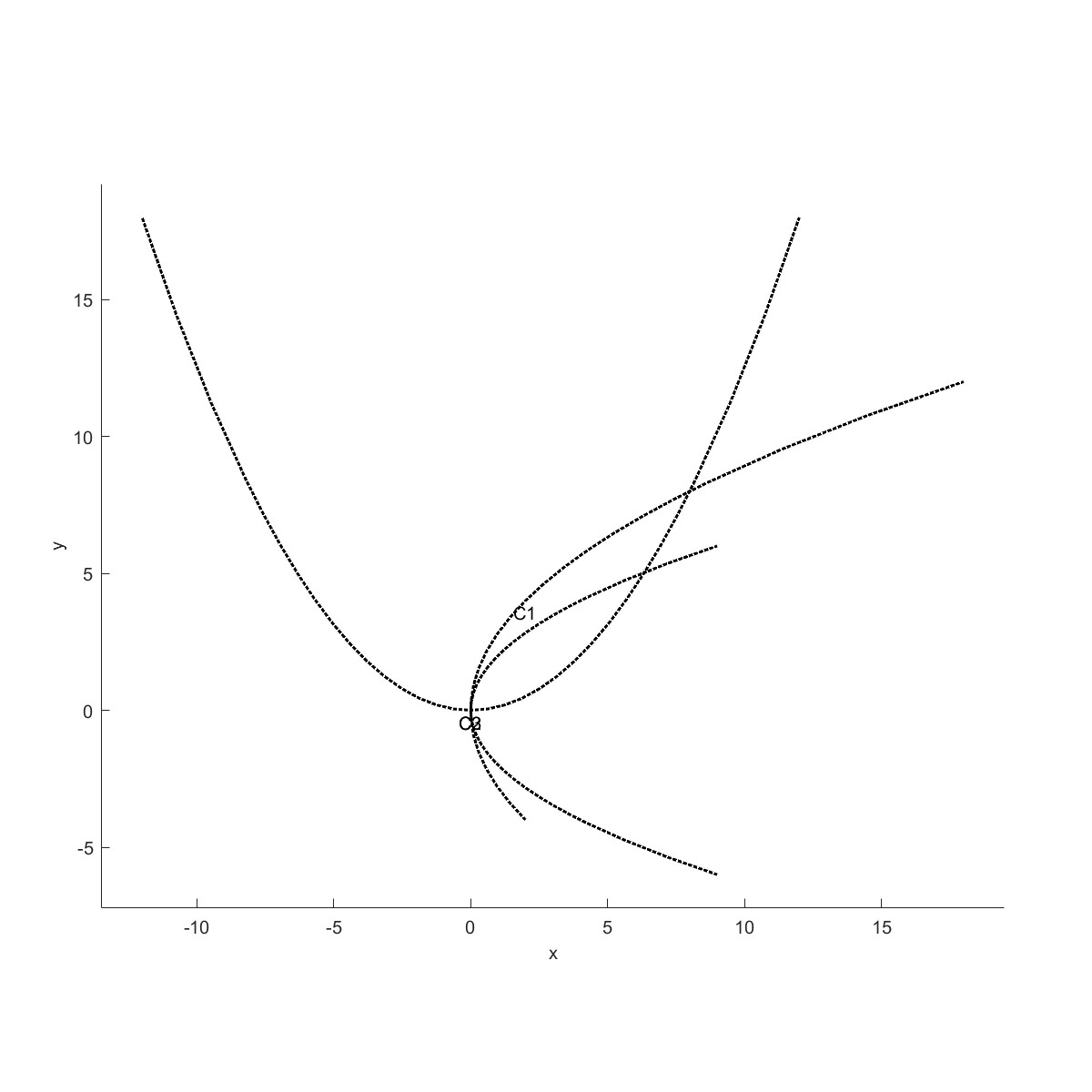双曲线	抛物线

Calculate the boundary of points (Flag=2)

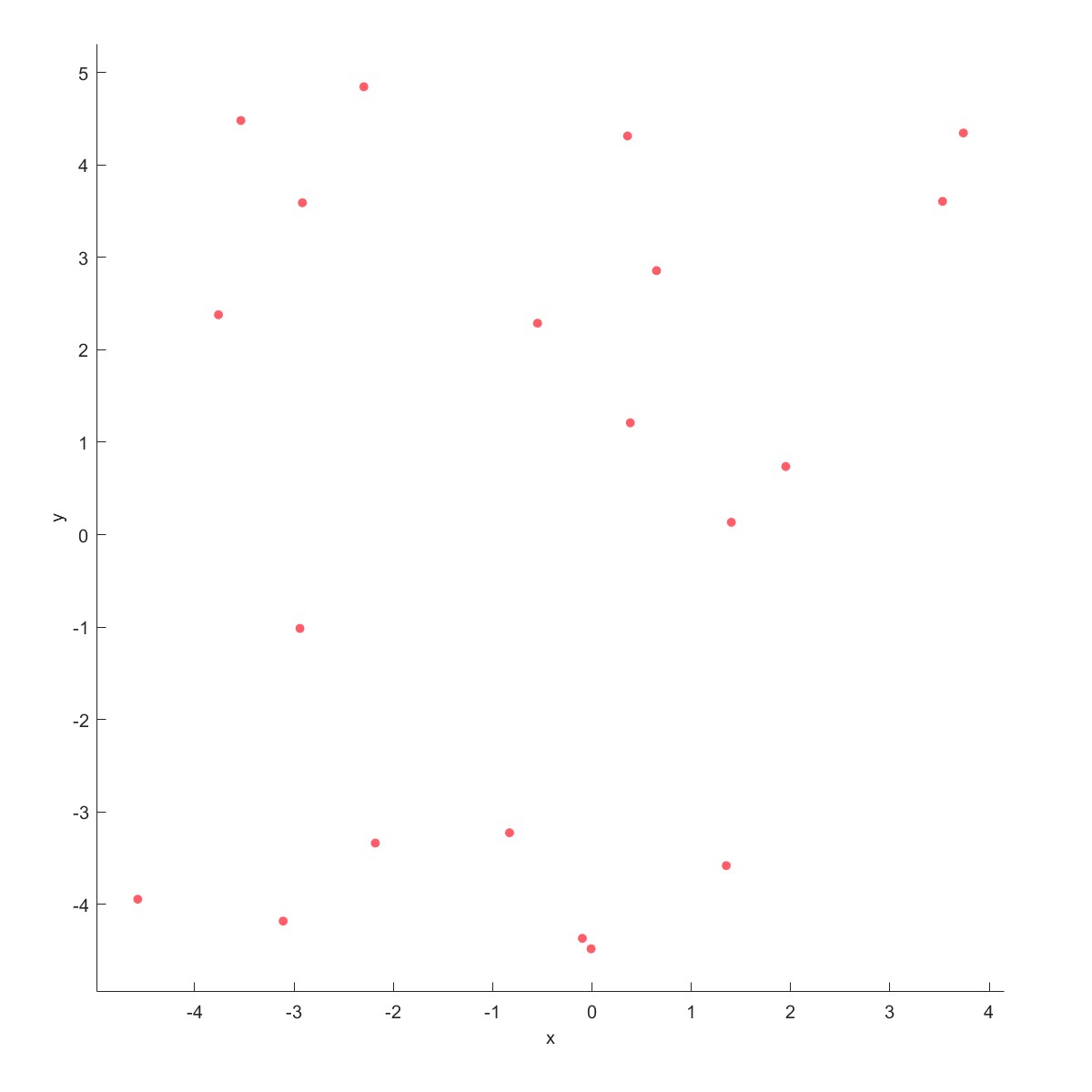
Boundary用来计算点集的边界，调整松弛因子可得到不同的边界曲线。

x1=-5 + (5+5)*rand(20,1);
y1=-5 + (5+5)*rand(20,1);
x2=-5 + (5+5)*rand(20,1);
y2=-5 + (5+5)*rand(20,1);
a=Point2D('Point Ass1');
a1=Point2D('Point Ass2');
a=AddPoint(a,x1,y1);
a1=AddPoint(a1,x2,y2);
Plot(a);
b=Line2D('Line Ass1','Compress',0);
b1=Line2D('Line Ass1','Compress',0);
b=Boundary(b,a);
b=Boundary(b,a,'scale',1);
b1=Boundary(b1,a1);
b1=Boundary(b1,a1,'scale',1);
Plot(b,'map','lch','color',1);
Plot(b1,'map','lch','color',1);
L=Layer('Layer 1');
L=AddElement(L,a,'Transform',[0,0,0,0,0,0]);
L=AddElement(L,a1,'Transform',[0,0,1,0,0,0]);
L=AddElement(L,b,'Transform',[0,0,0,0,0,0]);
L=AddElement(L,b1,'Transform',[0,0,1,0,0,0]);
Plot(L,'linesmerge',1,'equal',2);

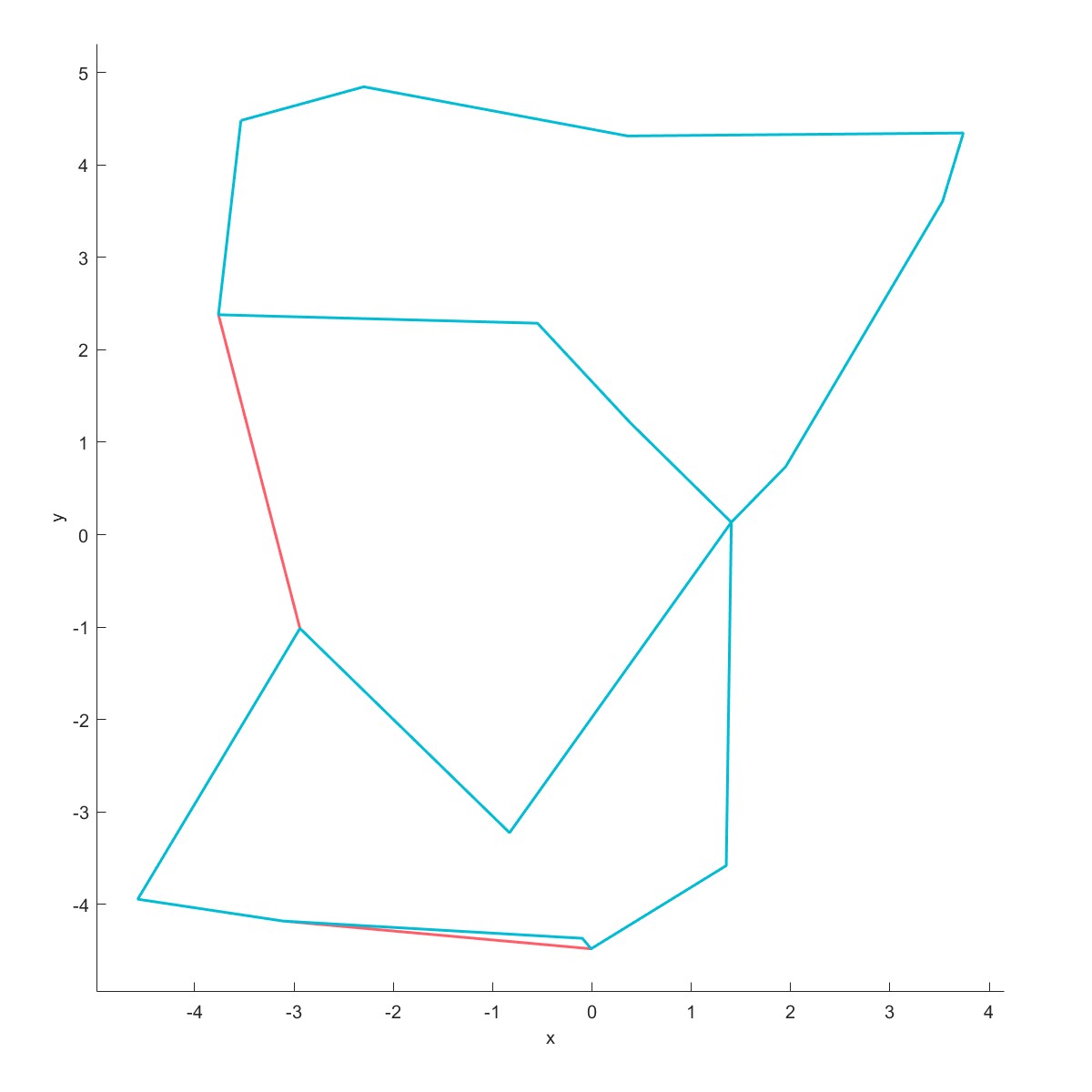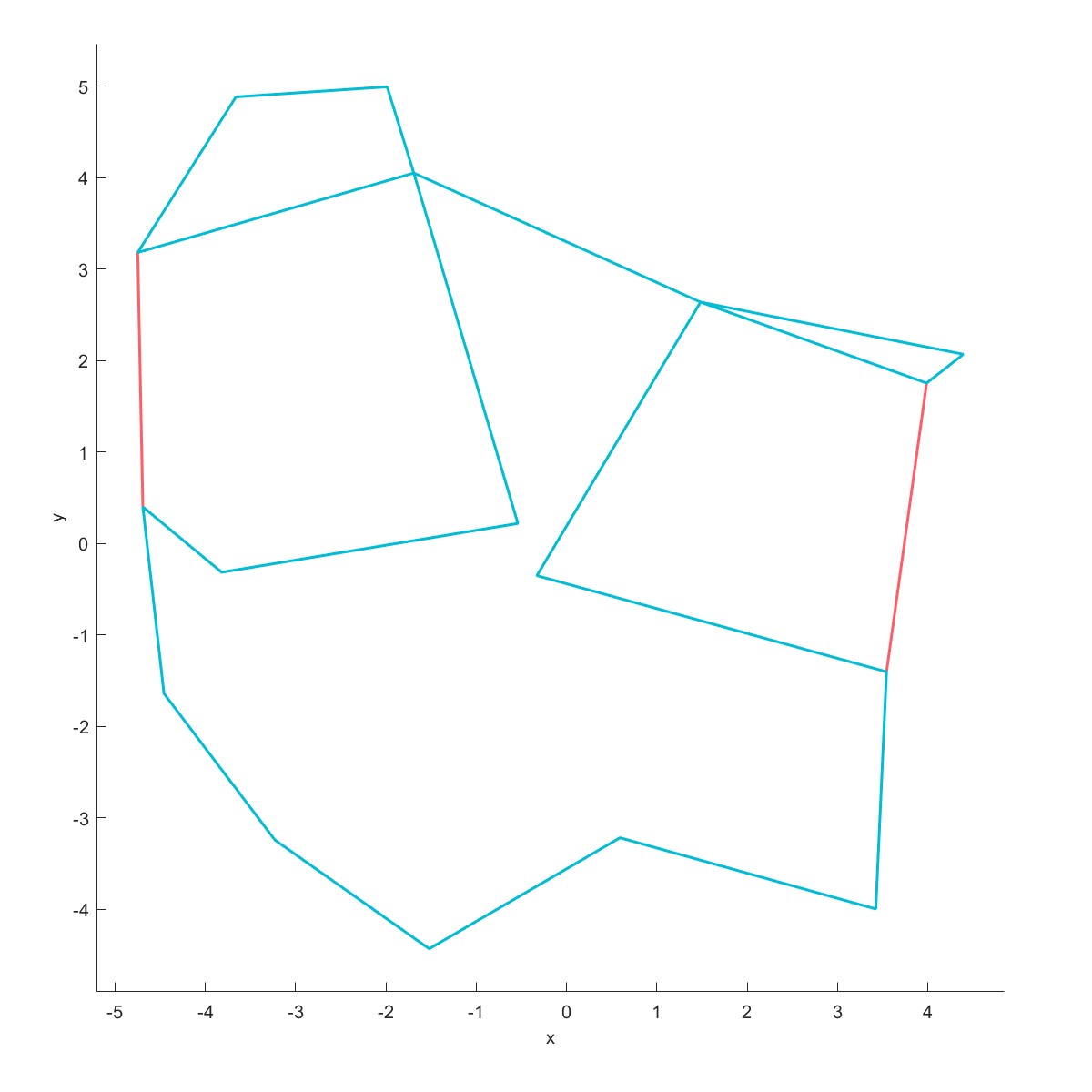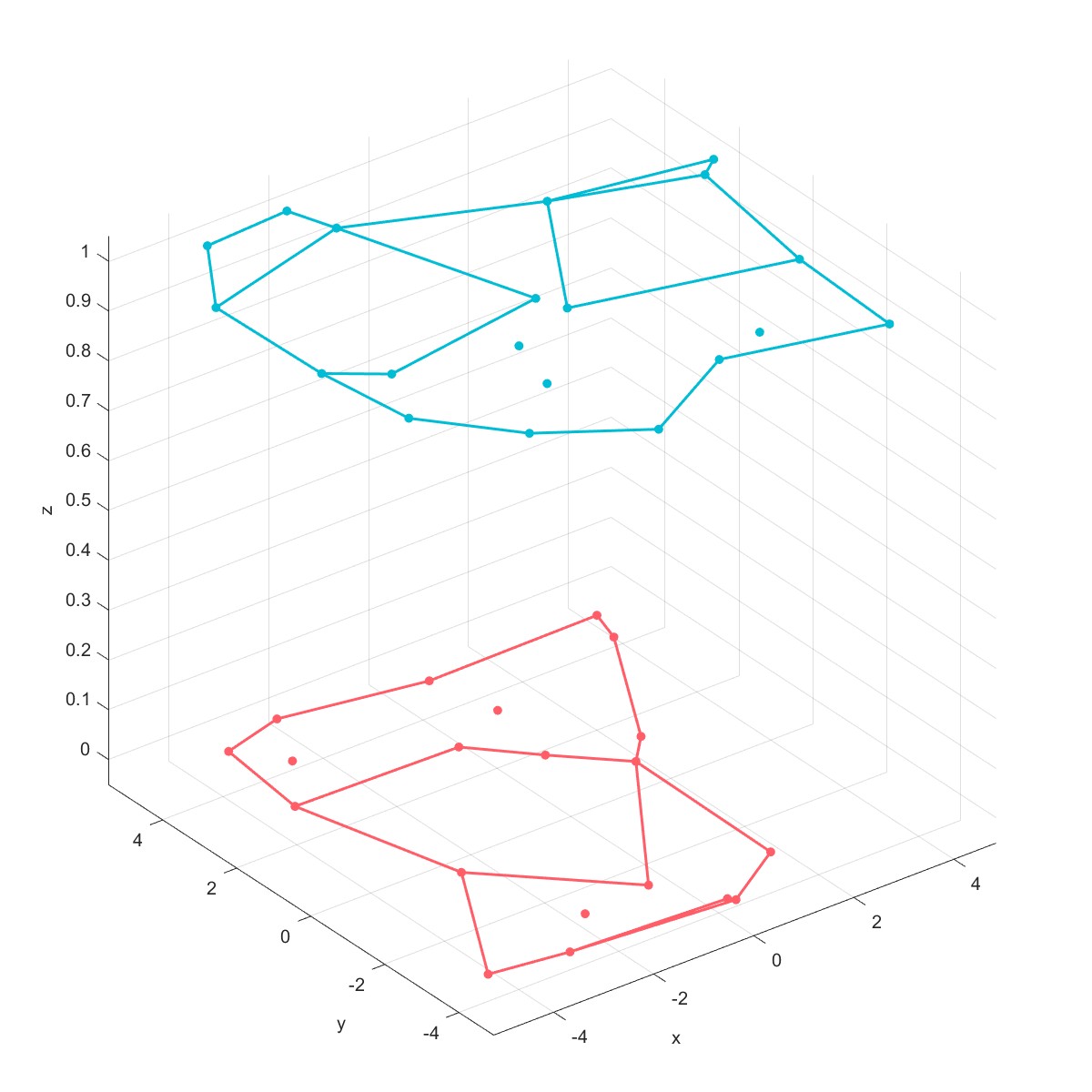Draw arrow (Flag=3)

绘制线段时，可将Arrow打开，并设置箭头的形式Form.

a=Point2D('Point Ass1');
for i=1:4
x=[i-1;i-0.5];
for j=1:3
y=[j-1;j-0.5];
a=AddPoint(a,x,y);
end
end
b=Line2D('Line Ass1','Arrow',1,'Form',(1:12)');
for i=1:12
b=AddLine(b,a,i);
end
Plot(b,'equal',1)

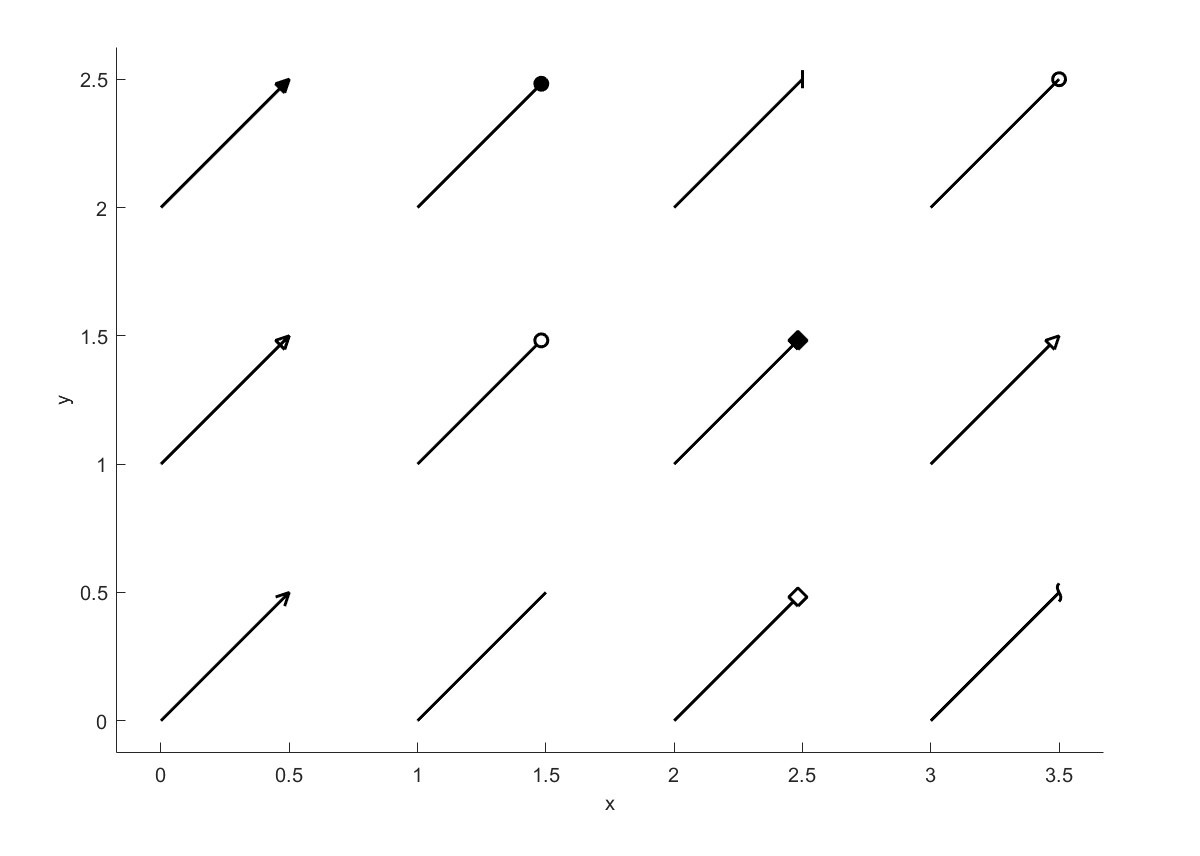
Polygon (Flag=4)

b=Line2D('Line Ass1','Arrow',1,'Adfac',0.01);
b=AddPolygon(b,1,10,'sang',90,'close',0);
b=Shift(b,1,2);
Plot(b,'equal',1,'crv',1);
Plot(b,'equal',1,'crv',2);

AddPolygon绘制多边形，打开close可得到封闭的多边形。

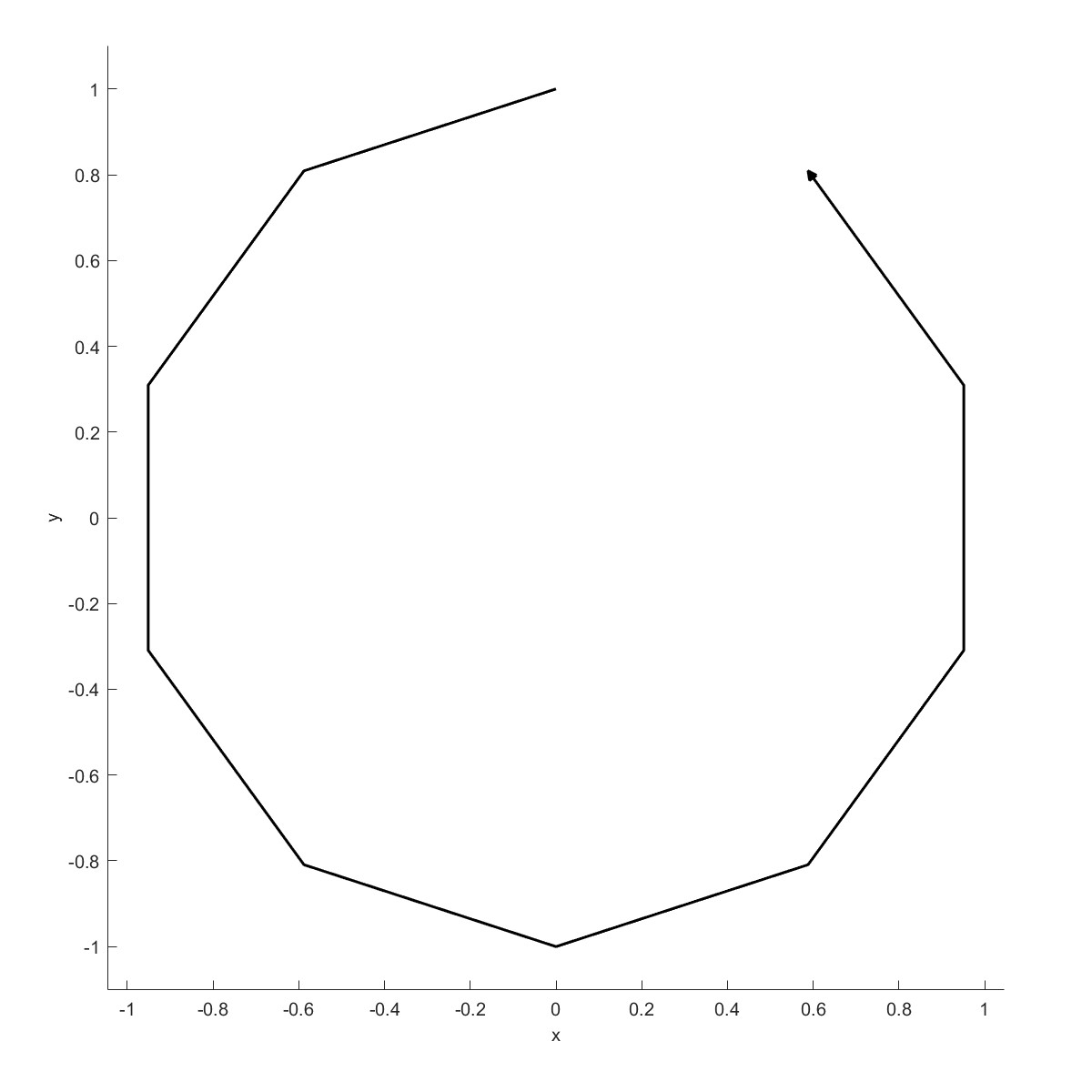
运用shift函数可以转换连接点位置，比如Shift(obj,1,2)代表将曲线1端点移动两个位置，得到效果如下。

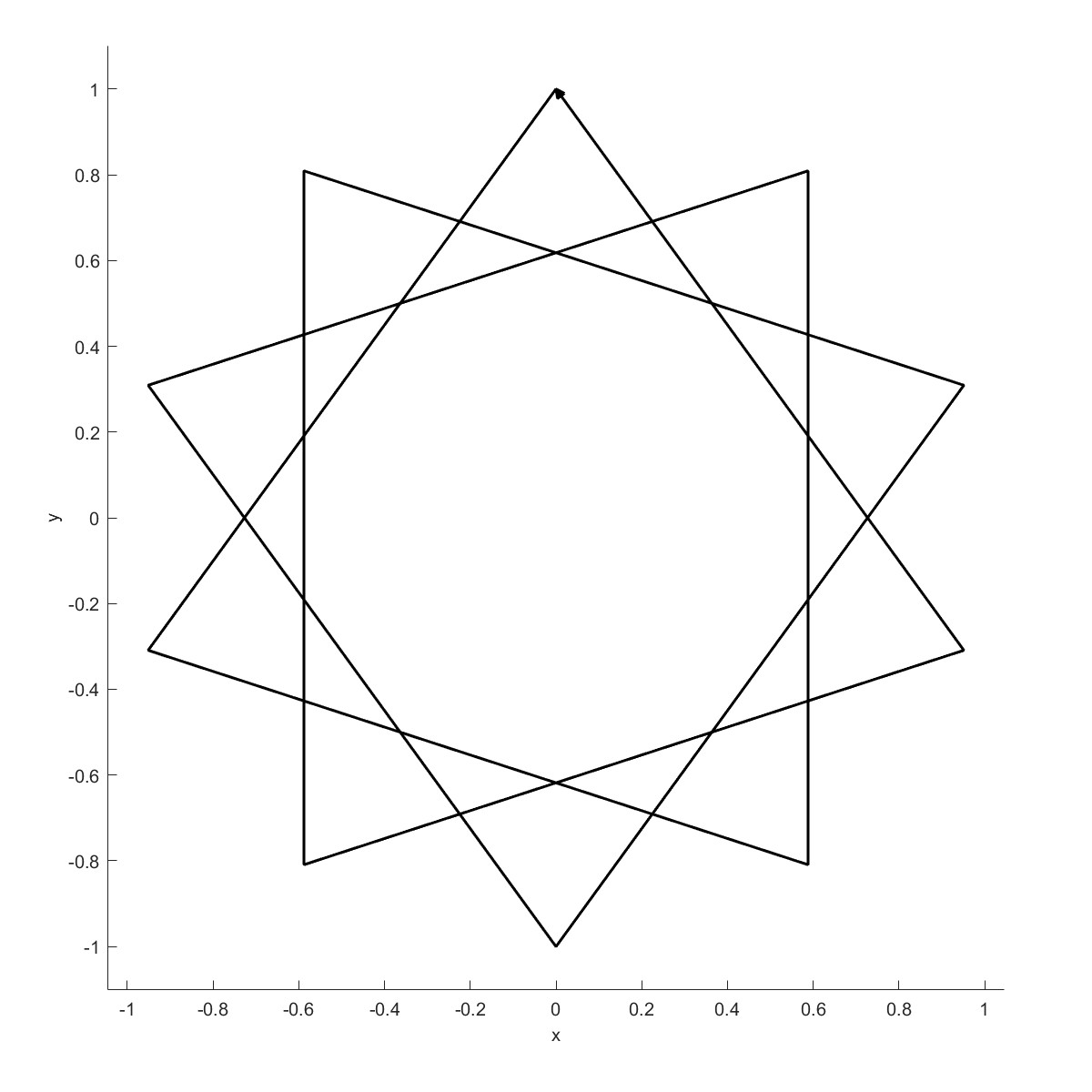
AddStar (Flag=5)

b=Line2D('Line Ass1');
b=AddStar(b,51,1,'sang',90,'close',1,'anglelimit',0);
Plot(b,'equal',1,'base_size',0.1);

AddStar可以列出n角星绘制的所有可能，下图是一个51角星所有绘制方法合成的一张图。

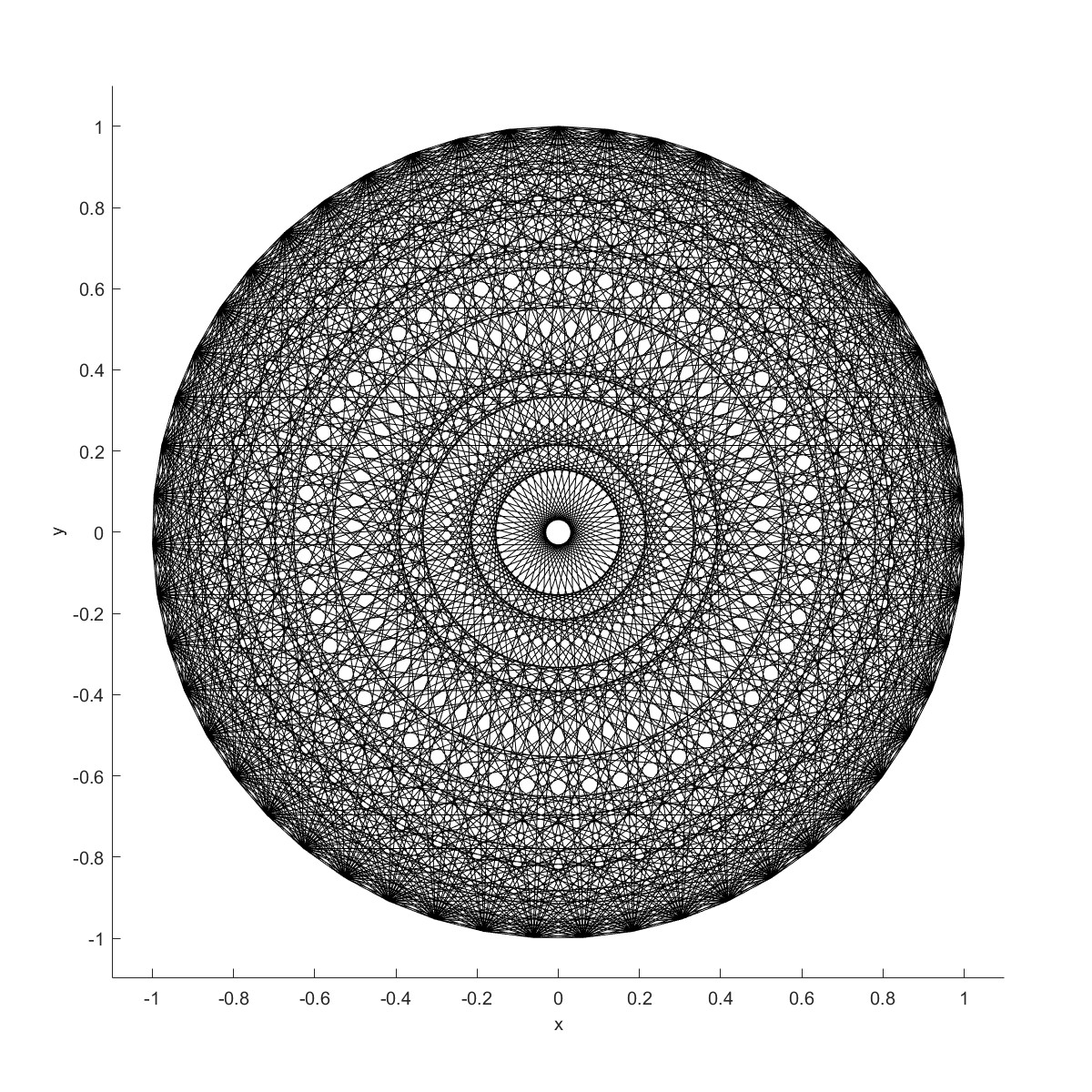
DeleteCurve (Flag=6)

b=Line2D('Line Ass1');
b=AddStar(b,11,1,'sang',90,'close',1);
Plot(b,'equal',1,'base_size',0.1);
b=DeleteCurve(b,1);
Plot(b,'equal',1,'base_size',0.1);

绘制11角星的所有可能，接下来把第一种方法删除，采用DeleteCurve来删除指定的曲线。

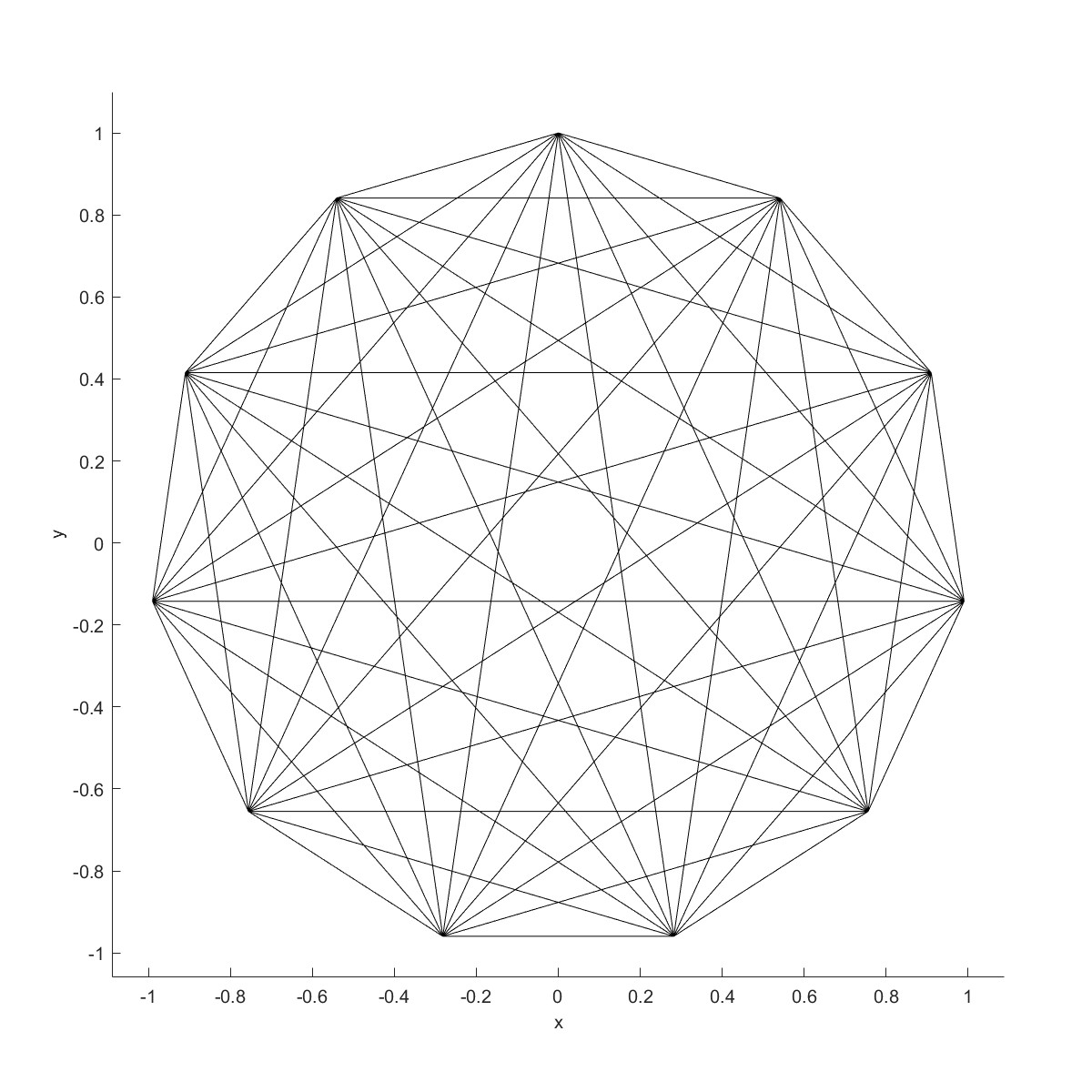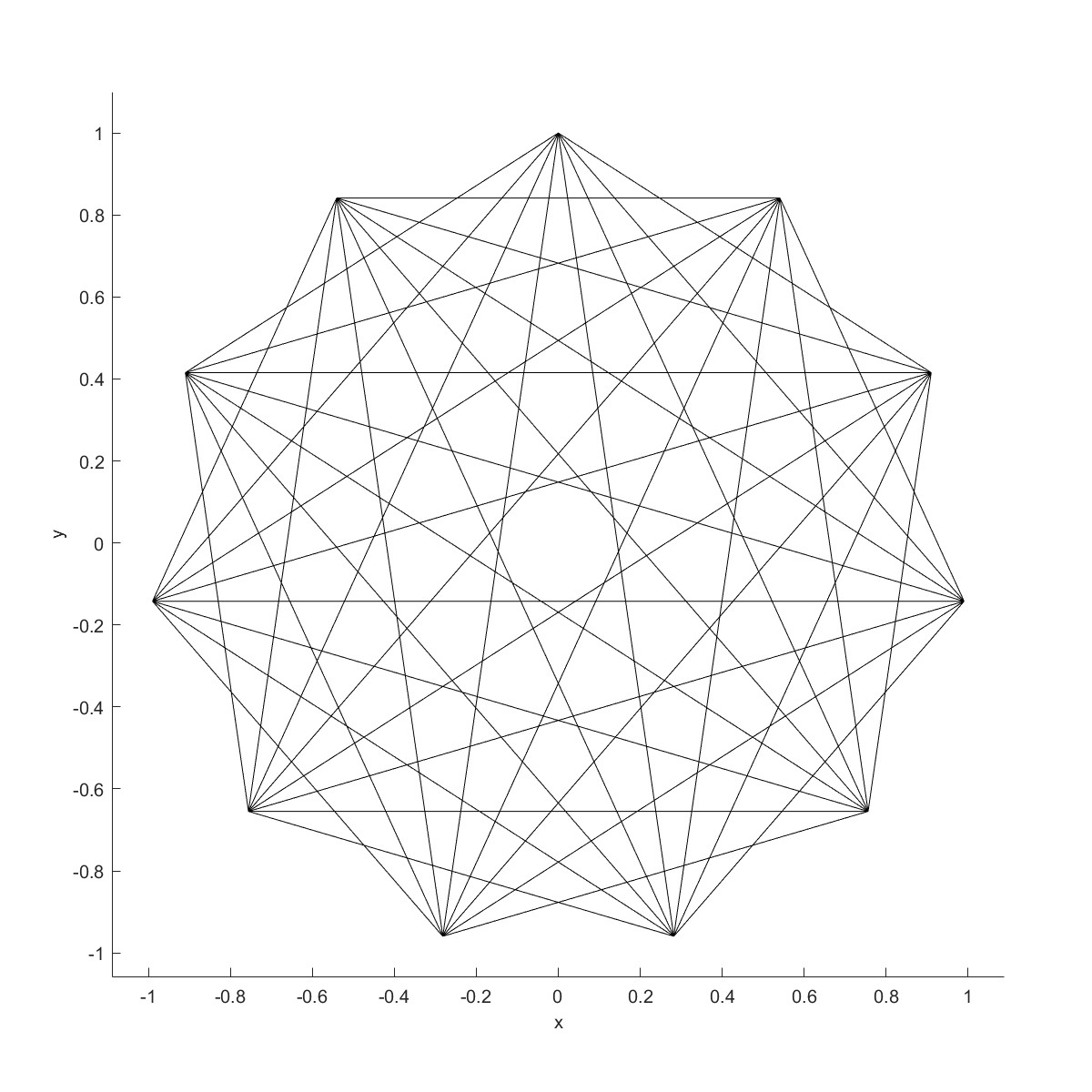Bounding box (Flag=7)

points=rand(100,2);
a=Point2D('Point Ass1');
a=AddPoint(a,points(:,1),points(:,2));
b=Line2D('Line Ass1');
b=BoundingBox(b,a);
L=Layer('Layer 1');
L=AddElement(L,a,'Transform',[0,0,0,0,0,0]);
L=AddElement(L,b,'Transform',[0,0,0,0,0,0]);
Plot(L,'linesmerge',1);

BoundingBox采用矩形的方式将所有的点包围。

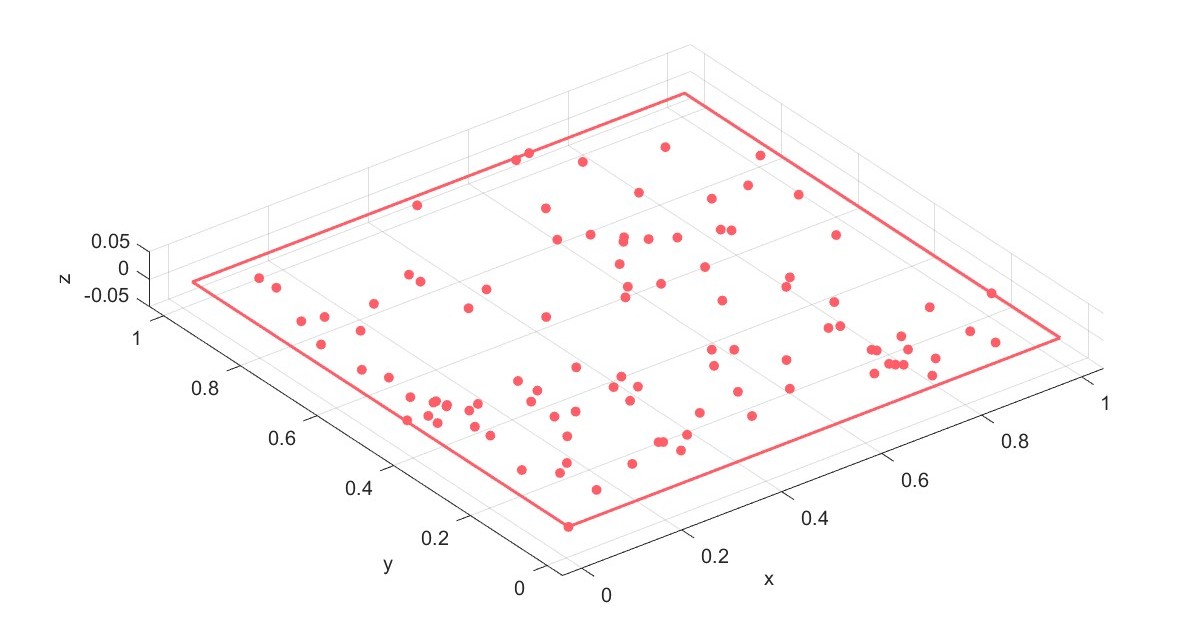
Create radius (Flag=8)

%% AddLine
x1=[0;5];y1=[0;5];
x2=[5;10];y2=[5;0];
a=Point2D('Point Ass1');
a=AddPoint(a,x1,y1);
a=AddPoint(a,x2,y2);
b=Line2D('Line Ass1');
b=AddLine(b,a,1);
b=AddLine(b,a,2);
Plot(b,'clabel',1);
b = CreateRadius(b,1,4);
Plot(b)

绘制两根相交的线段，采用CreateRadius在相交处生成倒角。

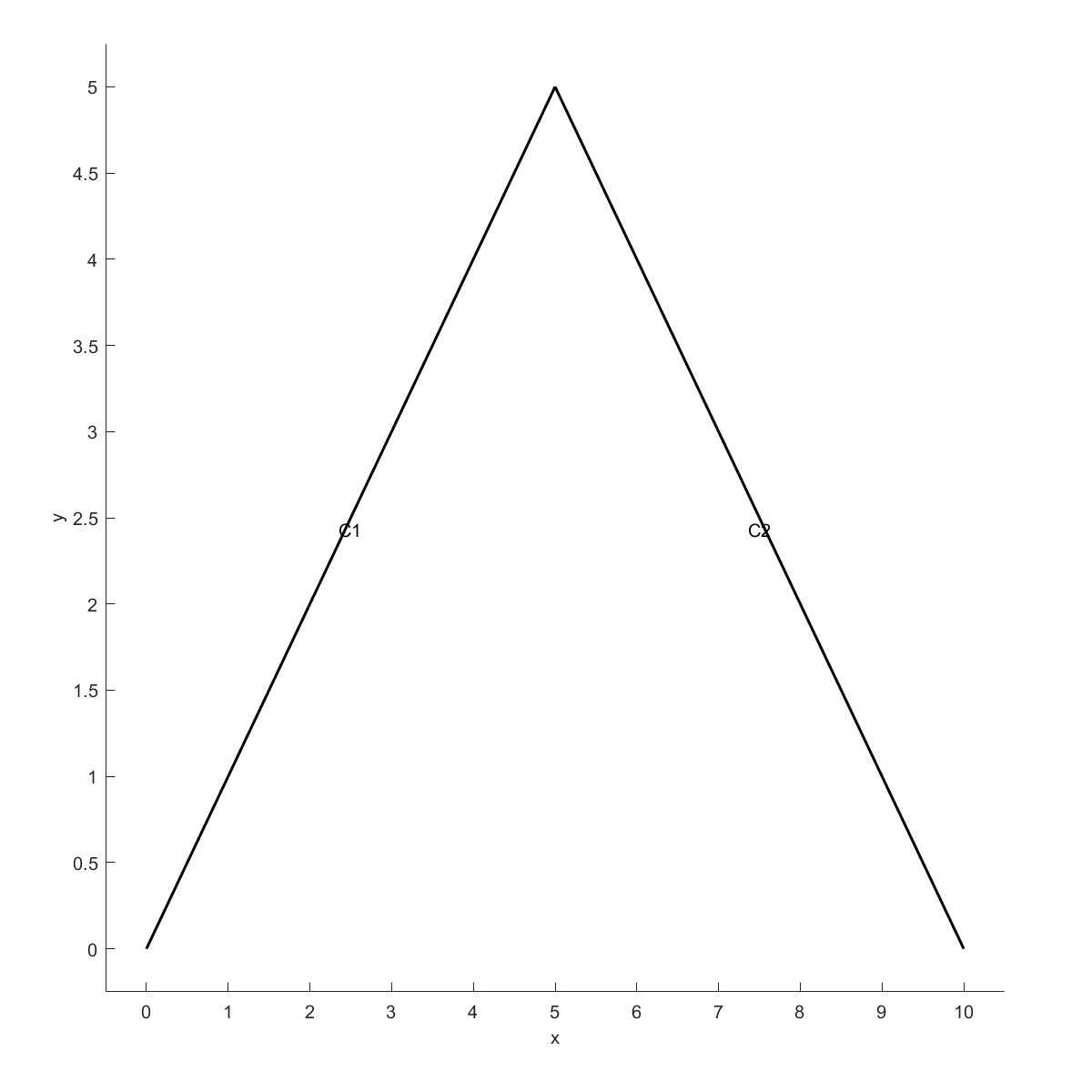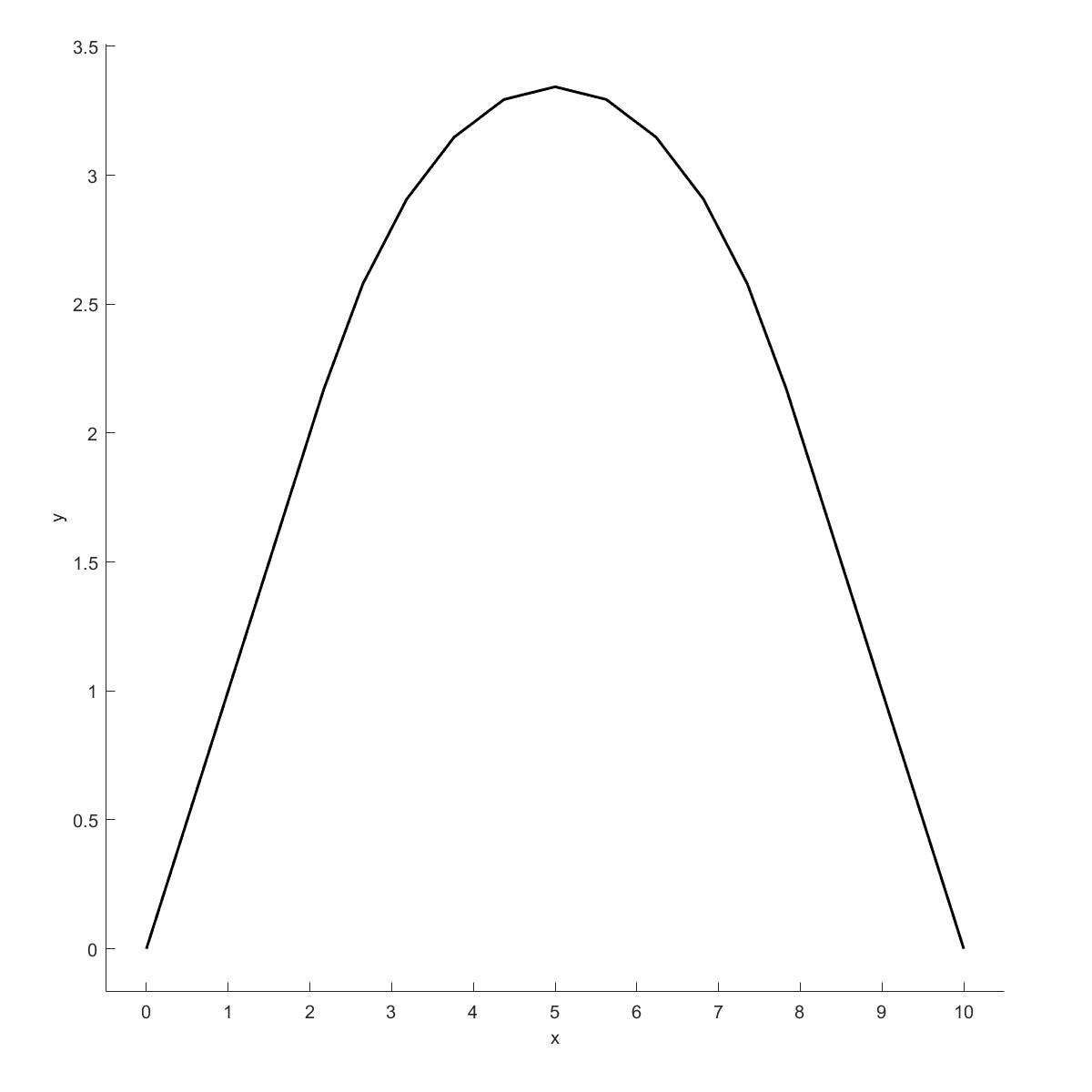Circle fit (Flag=9)

% Create data for a circle + noise
th = linspace(0,2*pi,20)';
R=1.1111111;
sigma = R/10;
x = R*cos(th)+randn(size(th))*sigma;
y = R*sin(th)+randn(size(th))*sigma;
a=Point2D('Point Ass1');
a=AddPoint(a,x,y);
Plot(a);
b=Line2D('Line Ass1');
[b,~,~,~]=CircleFit(b,a,1);
[b,~,~,~]=CircleFit(b,a,1,'method','Taubin');
Plot(b);

Circle fit将散点拟合成圆形，设有两种方式 Taubin method$^{[6]}$和Pratt method$^{[5]}$,两种方法测试下来差别不大。

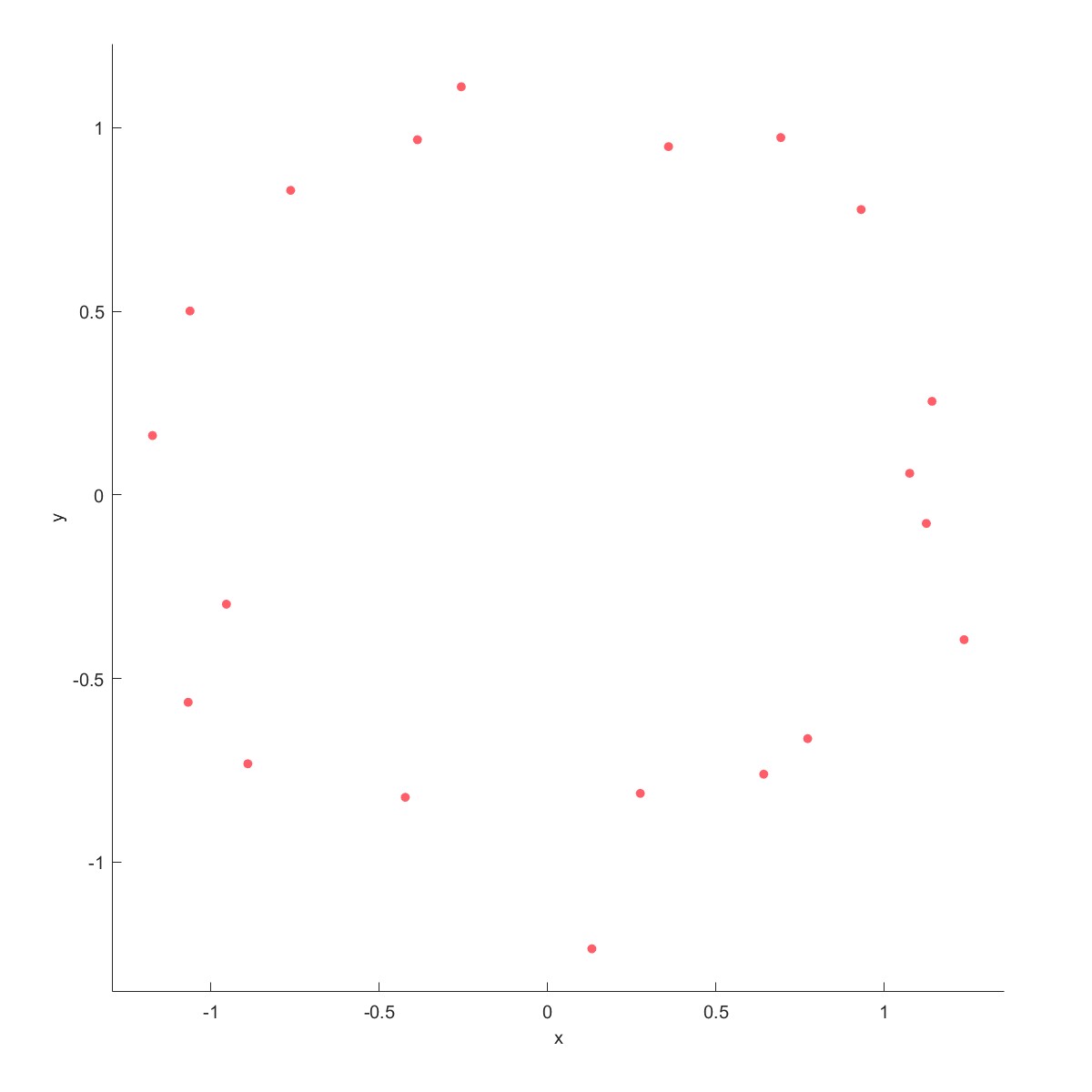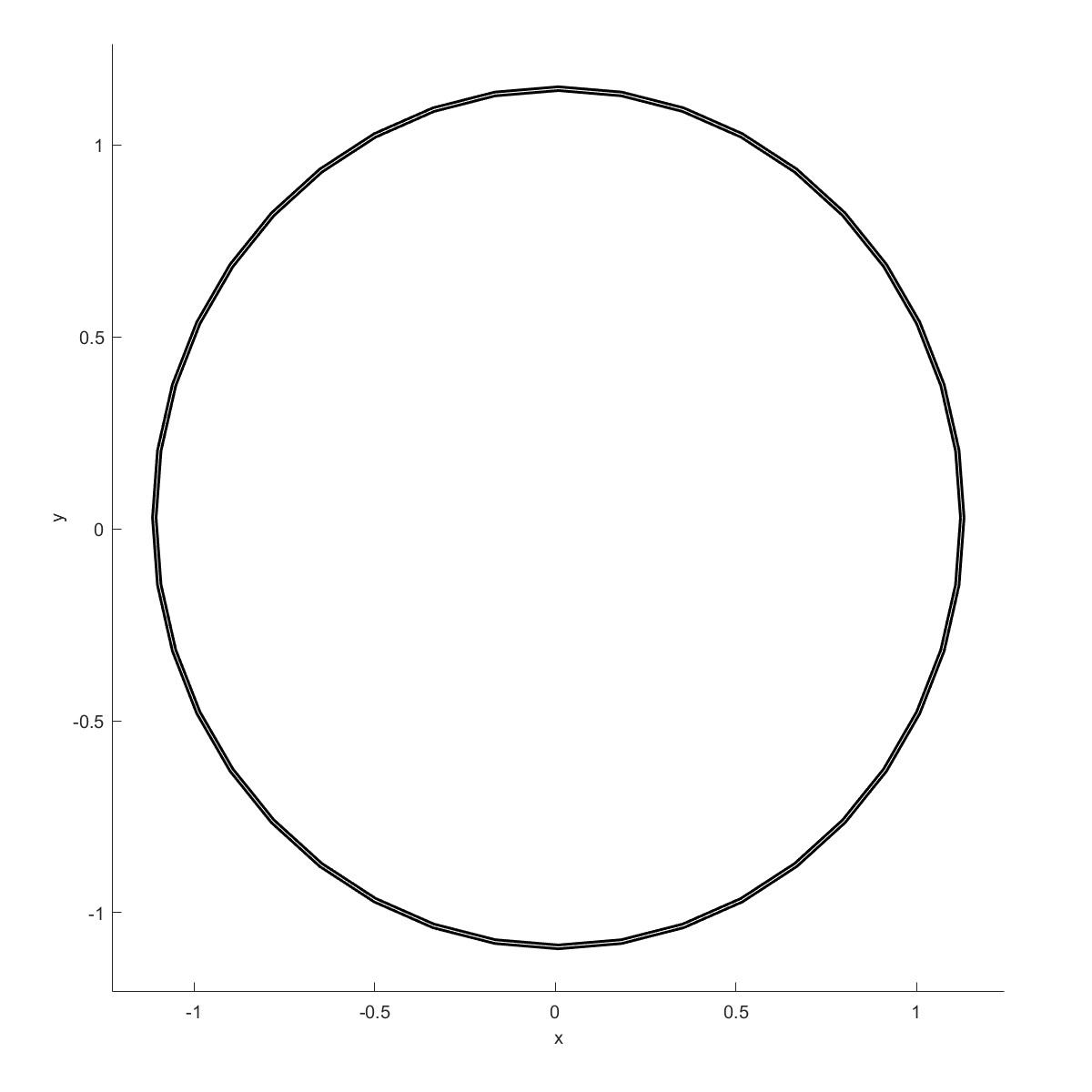Curve Intersection (Flag=10)

x=linspace(0,2*pi,100);
y1=sin(x);
y2=cos(x);
plot(x,y1);hold on
plot(x,y2);hold on
a=Point2D('Point Ass1');
a=AddPoint(a,x',y1');
a=AddPoint(a,x',y2');
b=Line2D('Line Ass1');
b=AddCurve(b,a,1);
b=AddCurve(b,a,2);
[x0,y0]=CurveIntersection(b,1,2);
plot(x0,y0,'k*')

CurveIntersection计算曲线的交点$^{[7]}$

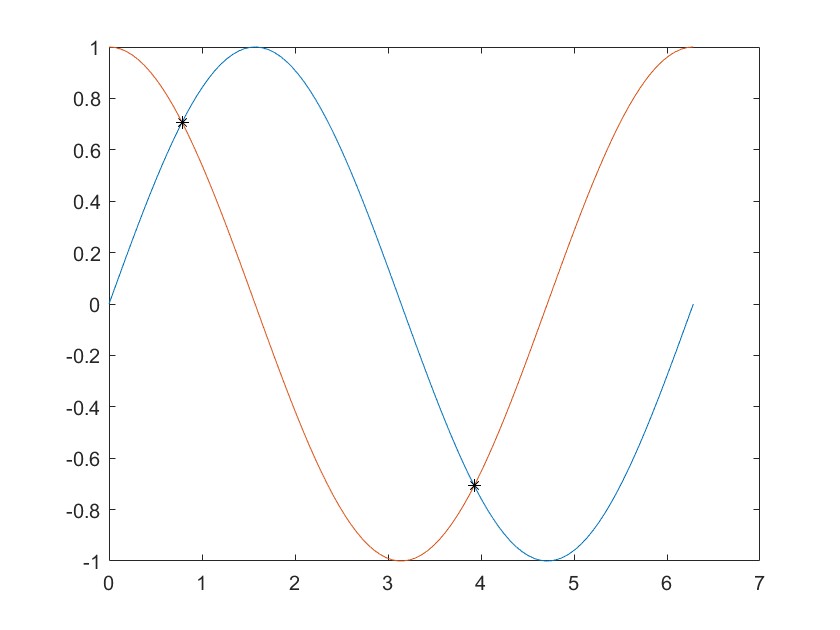
Add Round Polygon (Flag=11)

b=Line2D('Round Polygon');
b=AddRoundPolygon(b,5*sqrt(2),4,2,'sang',45);
Plot(b)

绘制圆角多边形。

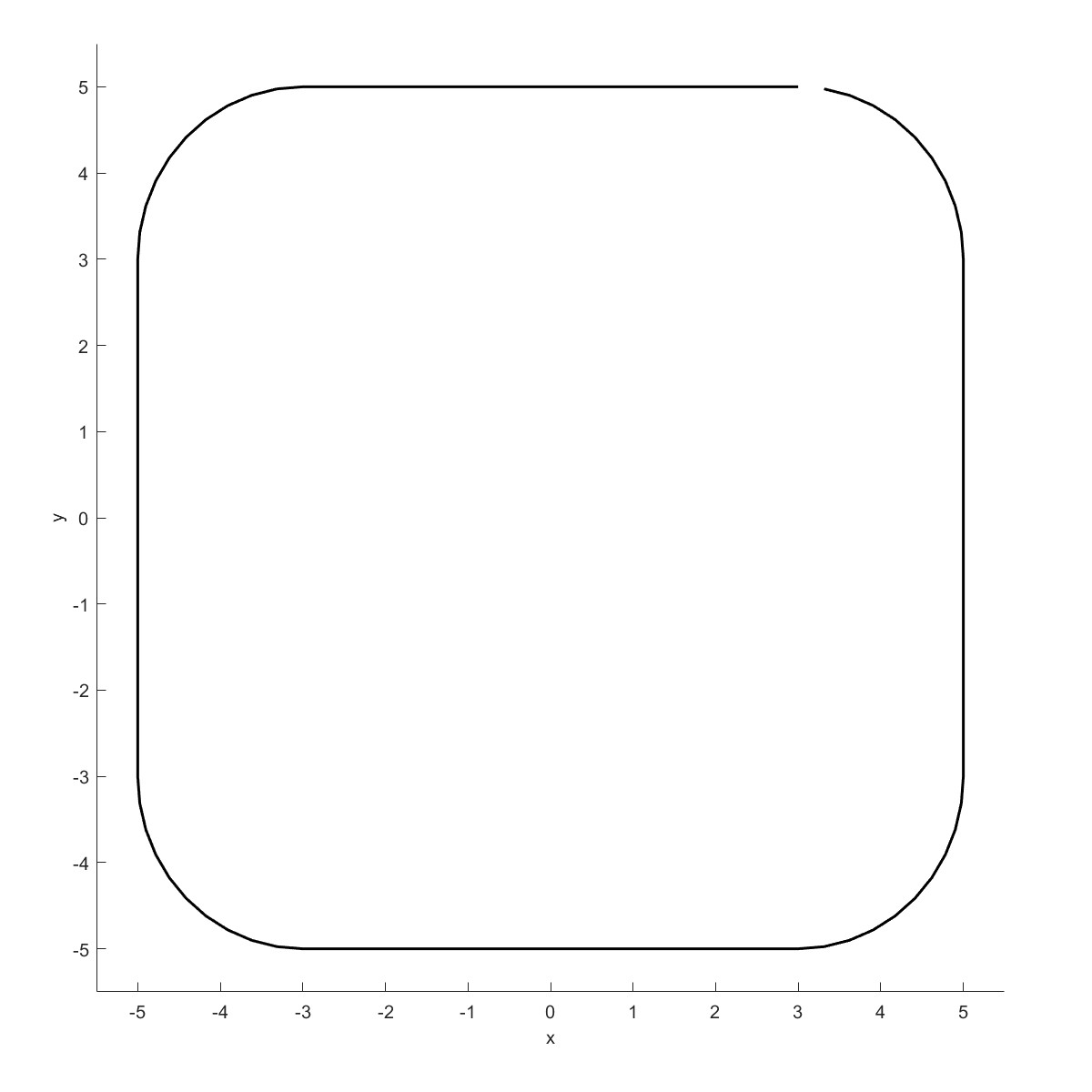
Plot Line2D in ParaView (Flag=12)

b=Line2D('Round Polygon');
b=AddRoundPolygon(b,5*sqrt(2),6,2);
Plot2(b)

Plot2可将曲线导出为VTK格式，并在Paraview中绘制。

Add Nurb curve (Flag=13)

Points = [0.5 1.5 4.5 3.0 7.5 6.0 8.5;
3.0 5.5 5.5 1.5 1.5 4.0 4.5]';
Knots=[0 0 0 1/10 2/5 3/5 4/5 1 1 1];
b=Line2D('Nurb Test');
b=AddNurb(b,Points,Knots);
Plot(b);
PlotNurbs(b,'coefs',1);

AddNurb绘制Nurb曲线，参考于Nurbs tool$^{[8]}$.

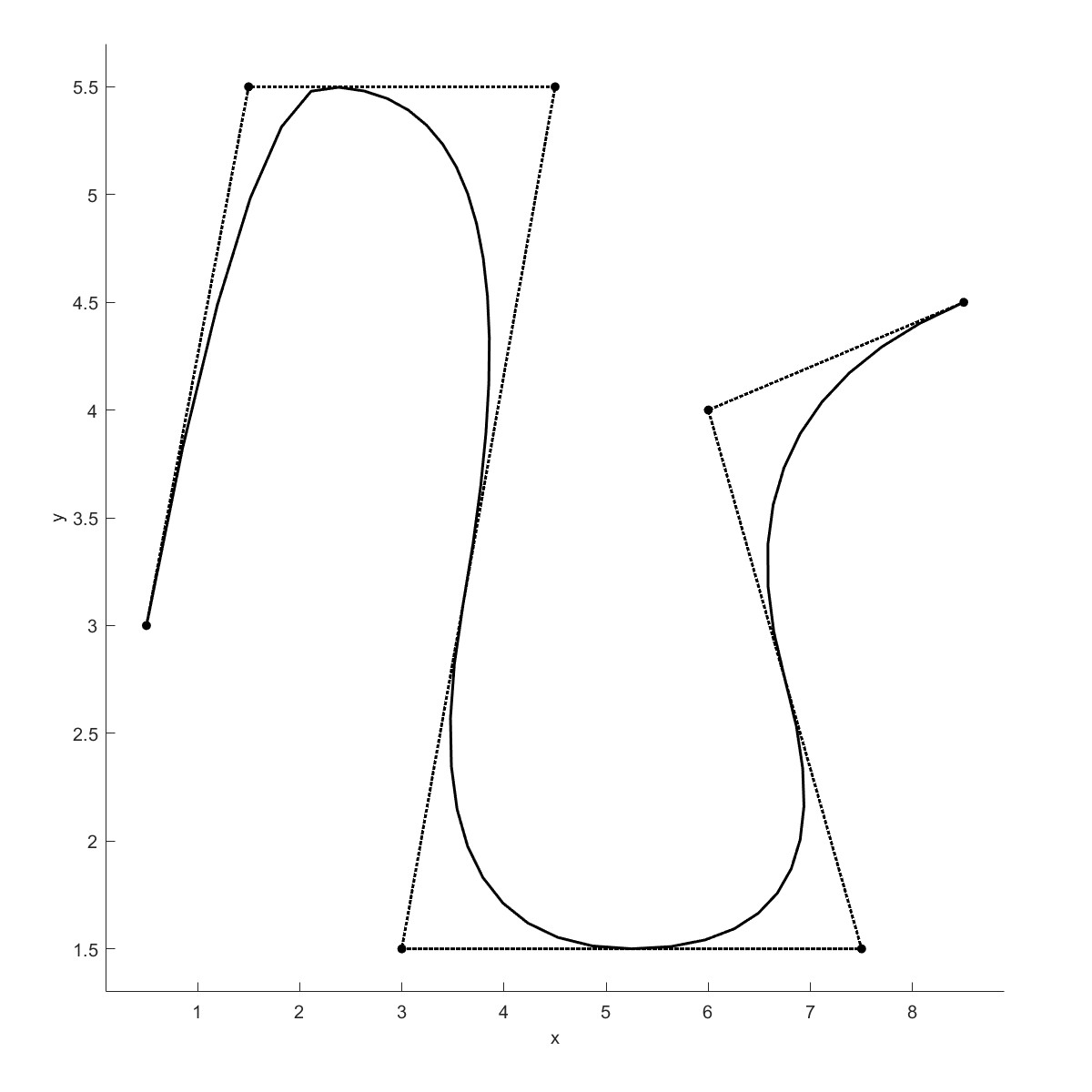
Convert to nurbs (Flag=14)

%% AddLine
x1=[-1;1];
y1=[-3;-3];
a=Point2D('Point Ass1');
a=AddPoint(a,x1,y1);
b=Line2D('Line Ass1');
b=AddLine(b,a,1);
%% AddCurve
x2=[0;0.15;0.3;-0.3;0];
y2=[0;-0.5;-1;-1;0];
a=AddPoint(a,x2,y2);
b=AddCurve(b,a,2);
%% AddCircle
x3=-3;y3=2;
x4=3;y4=2;
x5=0;y5=0;
a=AddPoint(a,x3,y3);
a=AddPoint(a,x4,y4);
a=AddPoint(a,x5,y5);
b=AddCircle(b,0.5,a,3);
b=AddCircle(b,0.5,a,4);
b=AddCircle(b,5,a,5);
%% AddEllipse
x6=0;y6=-3;
a=AddPoint(a,x6,y6);
b=AddEllipse(b,1,0.5,a,6,'rot',-90,'sang',-90,'ang',180);
%% AddSpline
x7=[-4;-3;-2];y7=[2.5;3;2.5];
a=AddPoint(a,x7,y7);
b=AddSpline(b,1,a,7);
%% AddBezier
x8=[4;3;2];y8=[2.5;3;2.5];
a=AddPoint(a,x8,y8);
b=AddBezier(b,a,8);
%% AddBspline
x9=[-1.5;0;1.5];y9=[3;3.5;3];
a=AddPoint(a,x9,y9);
b=AddBspline(b,3,a,9);
Plot(b,'equal',1);
for i=1:9
b=Convert2Nurb(b,i);
end
PlotNurbs(b,'equal',1,'coefs',0);

Convert2Nurb可将多段线转环为Nurb曲线。

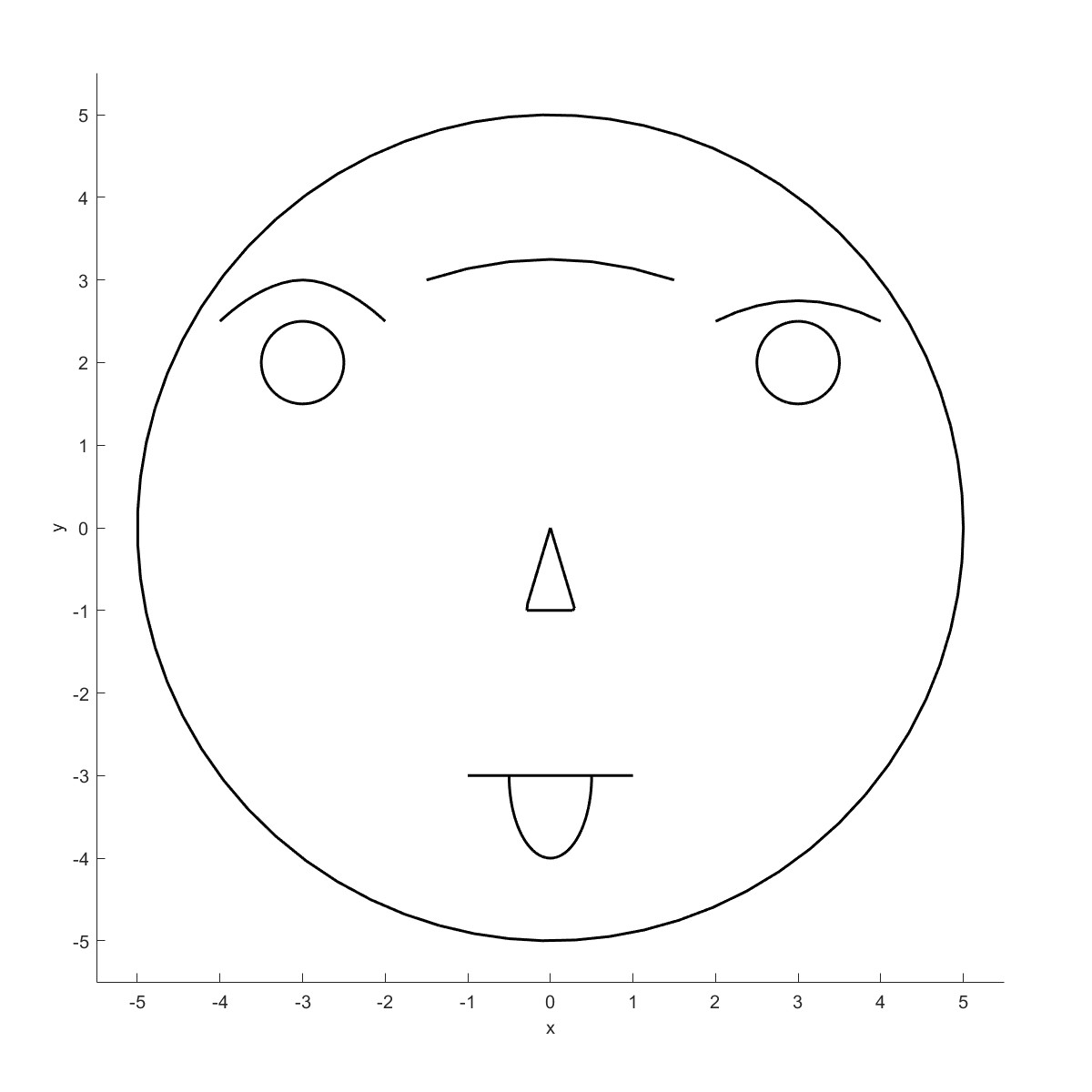
Add Cell data (Flag=15)

%% AddLine
x1=[-1;1];
y1=[-3;-3];
a=Point2D('Point Ass1');
a=AddPoint(a,x1,y1);
b=Line2D('Line Ass1');
b=AddLine(b,a,1);
%% AddCurve
x2=[0;0.15;0.3;-0.3;0];
y2=[0;-0.5;-1;-1;0];
a=AddPoint(a,x2,y2);
b=AddCurve(b,a,2);
%% AddCircle
x3=-3;y3=2;
x4=3;y4=2;
x5=0;y5=0;
a=AddPoint(a,x3,y3);
a=AddPoint(a,x4,y4);
a=AddPoint(a,x5,y5);
b=AddCircle(b,0.5,a,3);
b=AddCircle(b,0.5,a,4);
b=AddCircle(b,5,a,5);
%% AddEllipse
x6=0;y6=-3;
a=AddPoint(a,x6,y6);
b=AddEllipse(b,1,0.5,a,6,'rot',-90,'sang',-90,'ang',180);
%% AddSpline
x7=[-4;-3;-2];y7=[2.5;3;2.5];
a=AddPoint(a,x7,y7);
b=AddSpline(b,1,a,7);
%% AddBezier
x8=[4;3;2];y8=[2.5;3;2.5];
a=AddPoint(a,x8,y8);
b=AddBezier(b,a,8);
%% AddBspline
x9=[-1.5;0;1.5];y9=[3;3.5;3];
a=AddPoint(a,x9,y9);
b=AddBspline(b,3,a,9);
b=AddCellData(b,(1:9)');
Plot(b,'equal',1);
Plot2(b)

为曲线添加celldata，不同的曲线会有不同的色彩，celldata可以为计算分析中得到的值。

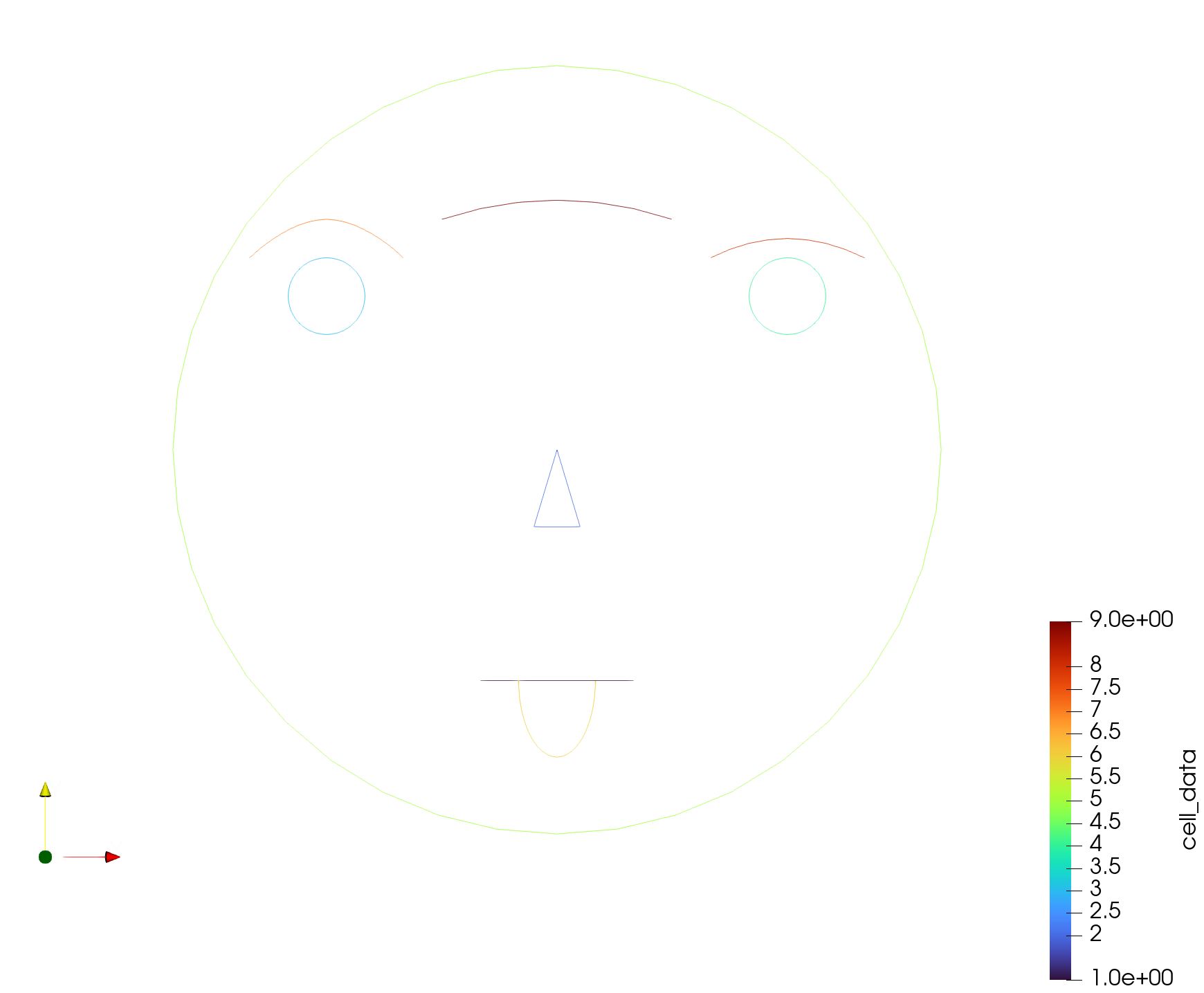
Max Inscribed Circle (Flag=16)

b=Line2D('Round Polygon');
b=AddRoundPolygon(b,5*sqrt(2),4,2);
b=MaxInscribedCircle(b,1);
Plot(b)

计算最大内切圆$^{[9]}$

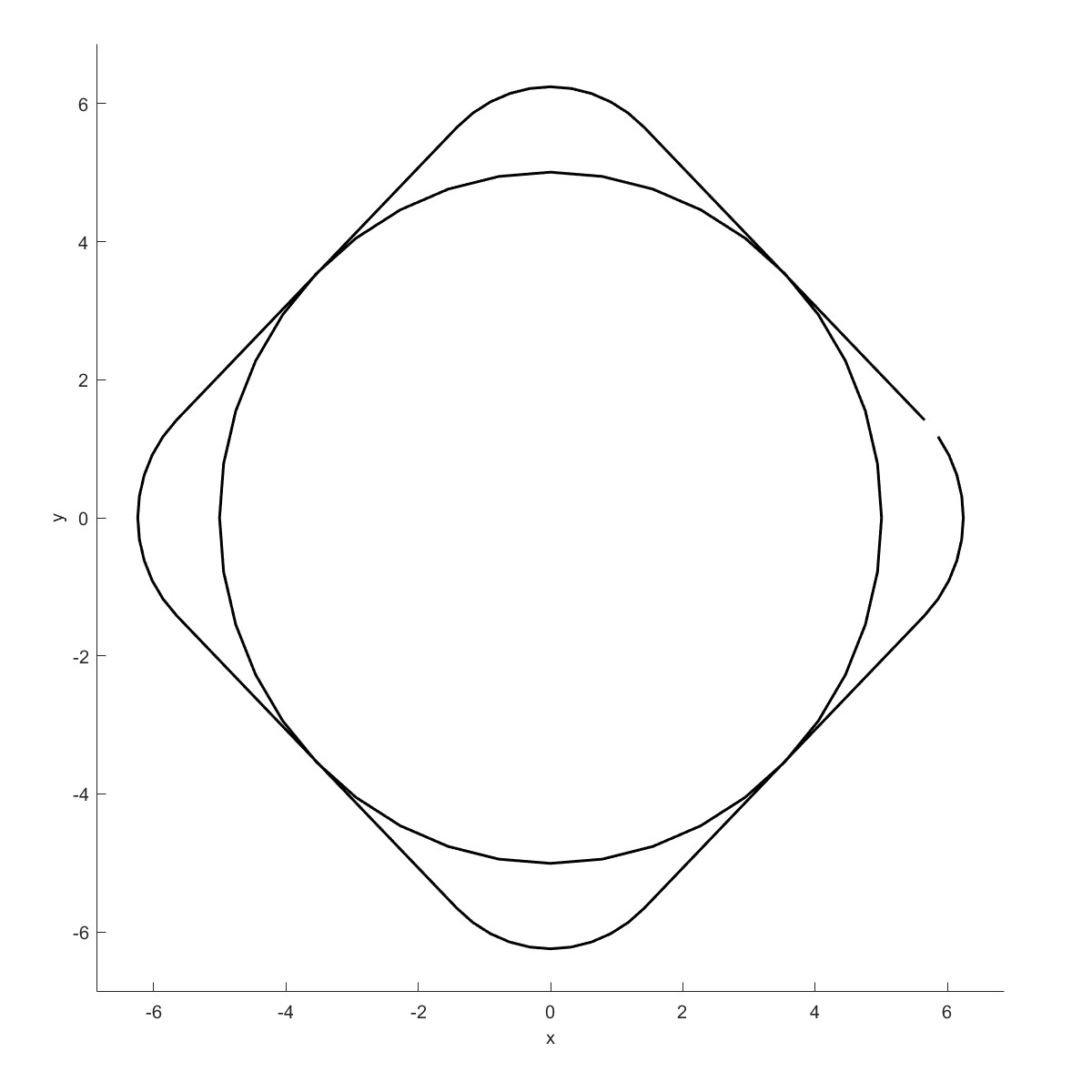
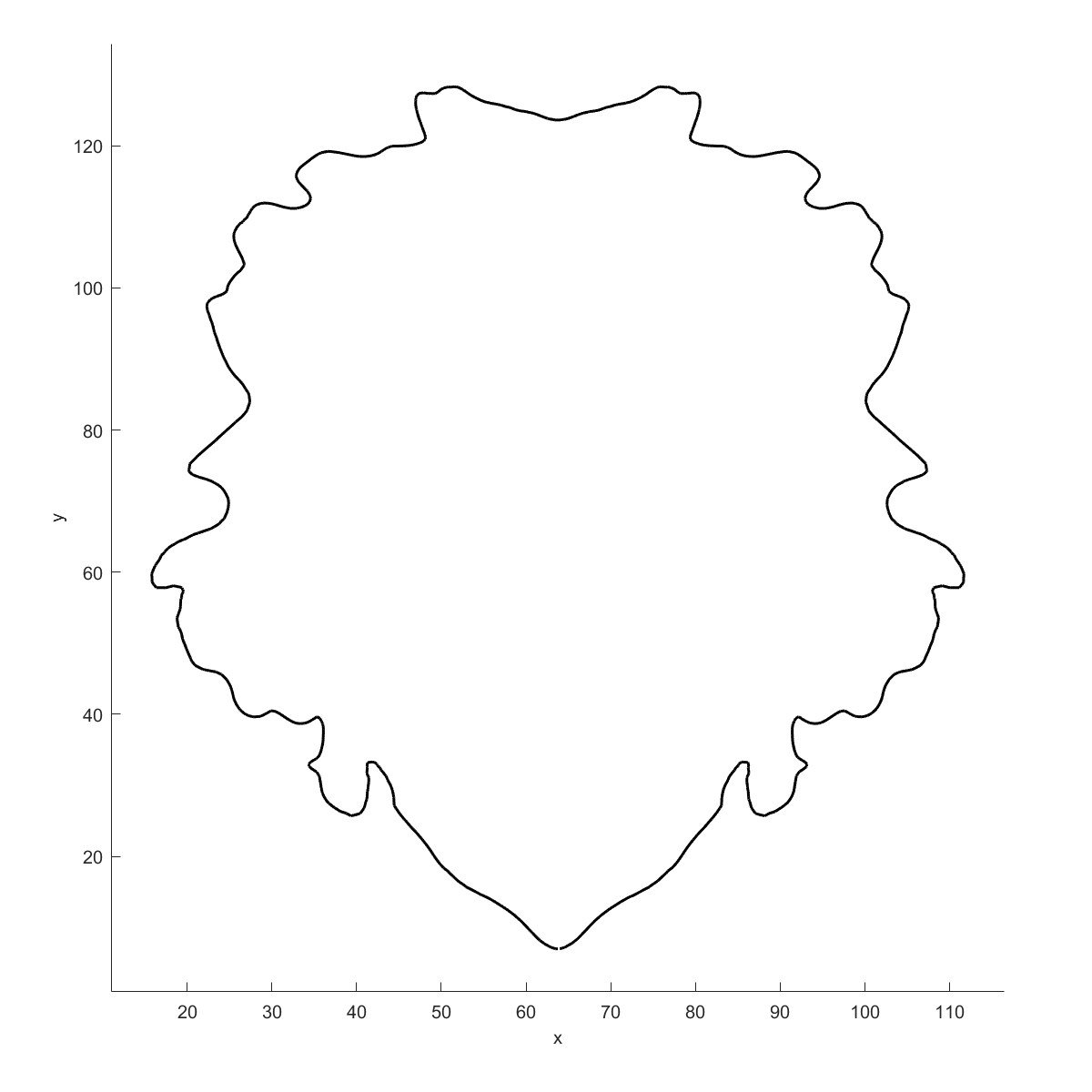
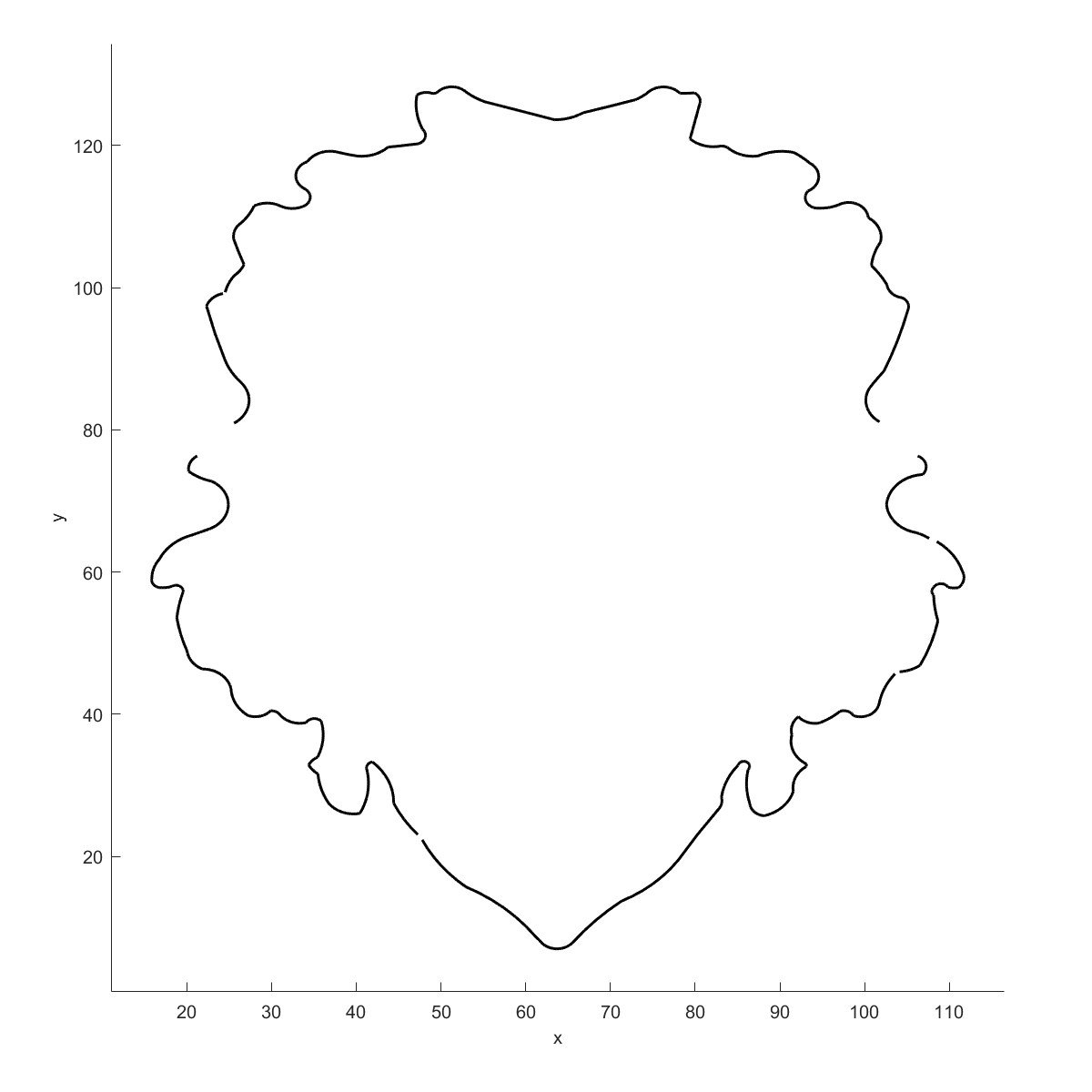
ArchFit (Flag=17)

load N_5 N_5
a=Point2D('Point Ass');
a=AddPoint(a,N_5(:,1),N_5(:,2));
b=Line2D('Line Ass');
b=AddCurve(b,a,1);
Plot(b);
bFit=ArchFit(b,1,0.1,4,1.7);
Plot(bFit)

将曲线用圆弧来拟合$^{[10]}$，在切割加工的场景下会有很多应用。

CheatTable

Name	Varargin	Description
AddBezier(obj,Point2D,P)		AddbBezier curve
AddBspline( obj, c, Point2D, P )		Add bspline curve
AddCellData(obj,Data)		Add cell data to curve
AddCircle(obj,r,Point2D,P)	‘sang’,’ang’,’seg’	Add circle
AddCurve(obj,Point2D,P)		Add curve
AddEllipse( obj, a, b,Point2D,P)	‘rot’,’sang’,’ang’,’seg’	Add ellipse
AddHyperbola( obj, a, b,Point2D,P)	‘rot’,’t1’,’t2’	Add hyperbola
AddLine(obj,Point2D,P)		Add straight line
AddLineThickness(obj,id,Thickness,theta)	‘add’,’close’	Offset curve
AddNurb(obj,coefs,knots)	‘seg’	Add nurb curve
AddParabola(obj,f,Point2D,P)	‘rot’,’t1’,’t2’	Add parabola
AddPolygon(obj,r,seg)	‘sang’,’close’	Add polygon
AddRoundPolygon(obj,r,seg,fillet)	‘sang’	Add round polygon
AddSpline( obj, ctype, Point2D, P )	‘a1’,a2’,’s1’,’s2’	Add spline
AddStar(obj,N,r)	‘sang’,’close’,’anglelimit’	Add star
ArchFit(obj,LineNum,e,min_dots,max_dist)		Curve arch fit
Boundary(obj,PP)	‘scale’,’group’	Calculate boundary of points
BoundingBox(obj,PP)	‘group’	Calculate box boundary of points
CircleFit(obj,PP,P)	‘method’	Circle fit of points
Convert2Nurb( obj,CrvNum)	‘seg’	Convert poly curve to nurb curve
CreateRadius(obj,l1,Radius)		Round corner of curves
CurveIntersection(obj,l1,l2)		Calculate intersection of curves
DeleteCurve(obj,ic)		Delete curve
GetCurve(obj,id)		Get curve points
GetNcrv(obj)		Get total number of curve
GetNNurb(obj)		Get total number of nurb
Help(obj)		Open help file
MaxInscribedCircle(obj,LineNum)		Get the maximum inscribed circle that fits inside
Meshoutput(obj)		Output Line2D mesh
NrbEval(obj,nurbsnum,tt)		Evaluate a NURBS at parameteric points
Plot(obj)	‘grid’,’axe’,’clabel’,’styles’, ‘equal’,’crv’,’map’,’color’, ‘base_size’,’xlim’,’ylim’	Plot line2D object
Plot2(obj)		Plot line2D on paraview
PlotNurbs(obj)	‘grid’,’axe’,’clabel’,’styles’, ‘equal’,’crv’,’map’,’base_size’, ‘xlim’,’ylim’,’coefs’	Plot nurb curves
PolyCurve( obj, id)	‘hmax’,’opt’	Polynomal approx. of the curve
RebuildCurve(obj,num,n)	‘interPar’,’closeLoopOpt’, ‘spacingFlag’	Rebuild curve
Shift(obj,ic,seq)		Change the sequence of the lines
VTKWrite(obj)		Write VTK file of 2D

参考文献

[1] https://www.mathworks.com/matlabcentral/fileexchange/72573-fem19?s_tid=srchtitle
[2] https://www.researchgate.net/publication/335465380_FEM19_Quick_Startpdf
[3] https://www.researchgate.net/publication/335465632_FEM19_Examples_v01pdf
[4] https://www.researchgate.net/publication/335465623_FEM19_Manual_v01
[5] https://ww2.mathworks.cn/matlabcentral/fileexchange/22643-circle-fit-pratt-method?s_tid=srchtitle
[6] https://ww2.mathworks.cn/matlabcentral/fileexchange/22678-circle-fit-taubin-method?s_tid=srchtitle
[7] https://ww2.mathworks.cn/matlabcentral/fileexchange/11837-fast-and-robust-curve-intersections?s_tid=srchtitle
[8] https://ww2.mathworks.cn/matlabcentral/fileexchange/26390-nurbs-toolbox-by-d-m-spink?s_tid=srchtitle
[9] https://ww2.mathworks.cn/matlabcentral/fileexchange/71995-max_inscribed_circle?s_tid=srchtitle
[10] https://ww2.mathworks.cn/matlabcentral/fileexchange/68439-polyline-approximation-with-arcs-and-segments?s_tid=srchtitle

---

本网站基于Hexo 3-Hexz主题生成。如需转载请标注来源,如有错误请批评指正,欢迎邮件至 392176462@qq.com