Component
介绍
Component是一个部件抽象类,他提供了输入输出以及安全系数的接口,现有的机械结构计算都基于概率理论基础上的可靠度设计方法$^{[1][2][3][4]}$。
任何工程结构,不管其用途如何,总应考虑各种荷载在结构中产生的荷载效应S和结构本身的抗力R两个基本变量。当R>S时,结构处于安全状态;R=S时,结构处于极限状态;R<S时,结构处于失效状态。
针对载荷本身,我们可以将结构载荷分为几类:
- 永久荷载
- 可变荷载
- 偶然荷载
根据不同的载荷类型,考虑自身特点,以及空间、时间相关性等构建对应的可靠度参数,构建载荷效应S的方程。
对于材料,应基于不同的尺度予以考虑:
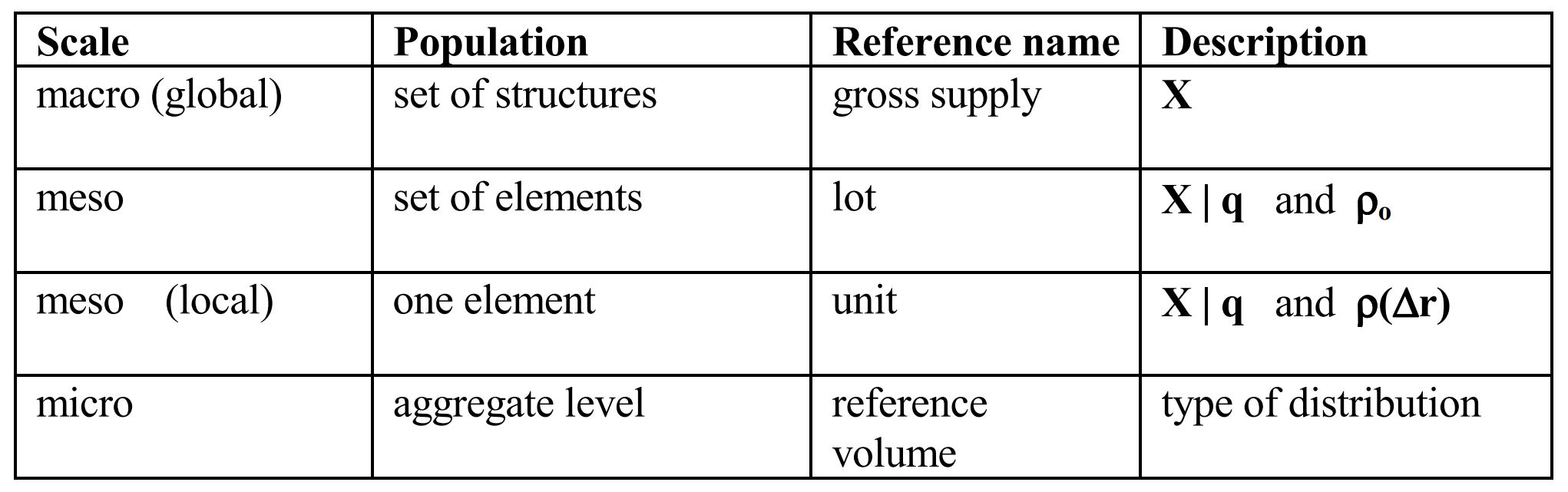
从微观到宏观,观测手段、测试方法不同,同时不同的破坏形式(脆性、延性、疲劳和冲击),对材料抗力的构建方式均不相同。
其他的因素例如结构重要性,心理因素等也应考虑到结构设计中。
为此在Baffalo中设计了抽象的部件类:
- input : 输入,可以是载荷,几何尺寸
- params : 参数, 默认的设置,材料等
- output : 输出,网格模型,关键设计参数
- baseline : 基准,部件须达到的设计基准
- capacity : 能力,部件的安全系数
案例
我们设计一个工程算法,输入a和b,定义比例系数p
输出安全系数S1:
$$
S1=(a+b)×p
$$
输出安全系数S2:
$$
S2=S1/1.2
$$
默认定义S1和S2的基础均为1,也就是说当S1和S2均大于1,我们认为结构安全。
classdef TestComponent < Component
% Class TestComponent
% Author: Xie Yu
properties(Hidden, Constant)
paramsExpectedFields = {
'p'
};
inputExpectedFields = {
'a'
'b'
};
outputExpectedFields = {
'c'
};
baselineExpectedFields = {
'S1'
'S2'
};
statesExpectedFields = {};
default_p=1;
base_S1=1;
base_S2=1;
end
methods
function obj = TestComponent(paramsStruct,inputStruct,varargin)
obj = obj@Component(paramsStruct,inputStruct,varargin);
obj.documentname='Test Component.html';
end
function obj = solve(obj)
a=obj.input.a;
b=obj.input.b;
p=obj.params.p;
c=(a+b)*p;
obj.output.c=c;
obj.capacity.S1=c;
obj.capacity.S2=c/1.2;
end
end
end
输入a=1,b=2,将S1的基准改为2
inputStruct.a=1;
inputStruct.b=2;
paramsStruct=struct();
baselineStruct.S1=2;
T= TestComponent(paramsStruct, inputStruct,baselineStruct);
T = T.solve();
disp(T.capacity.S1)
PlotStruct(T);
Help(T)
PlotCapacity(T);
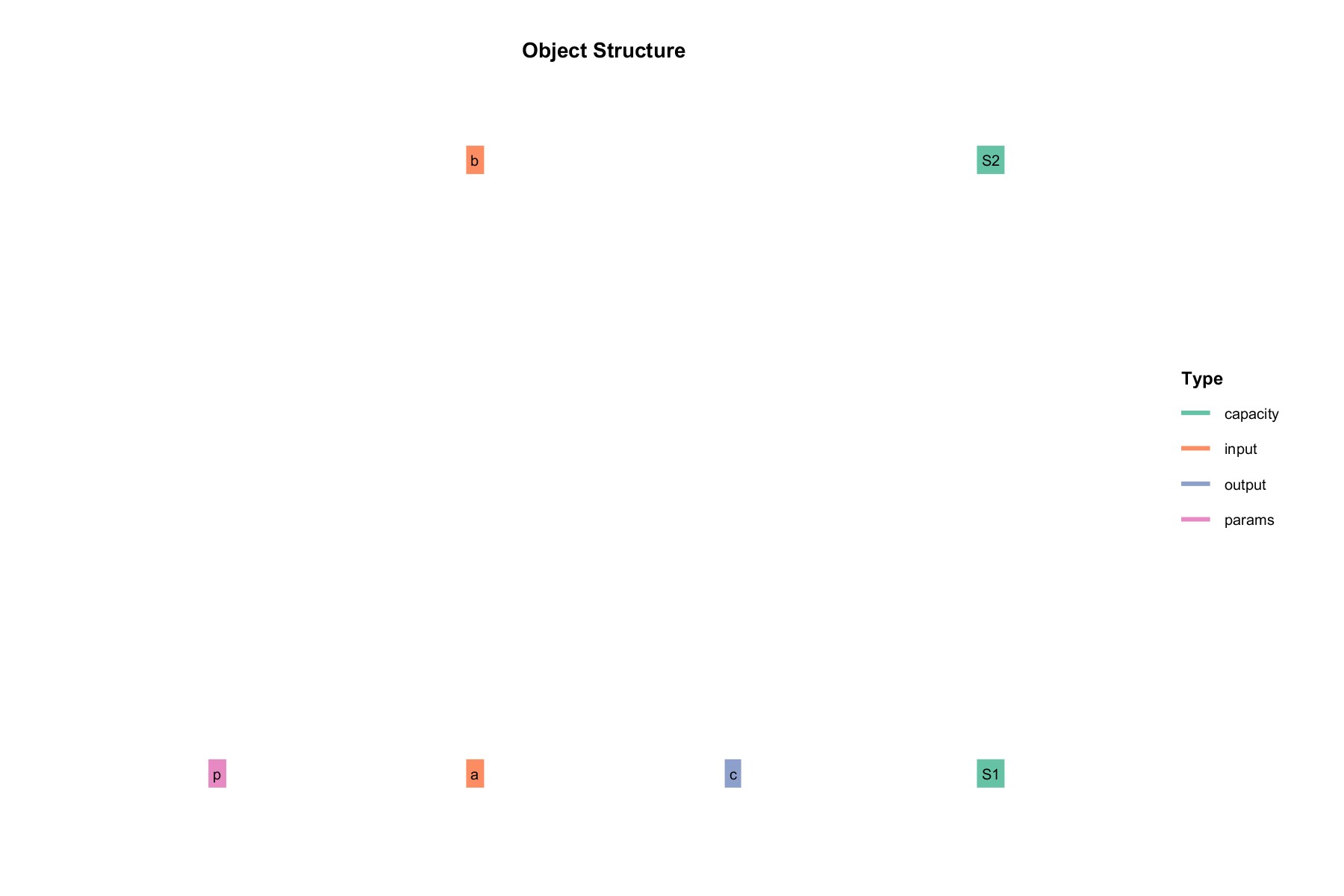
利用PlotStruct()函数查看部件结构:
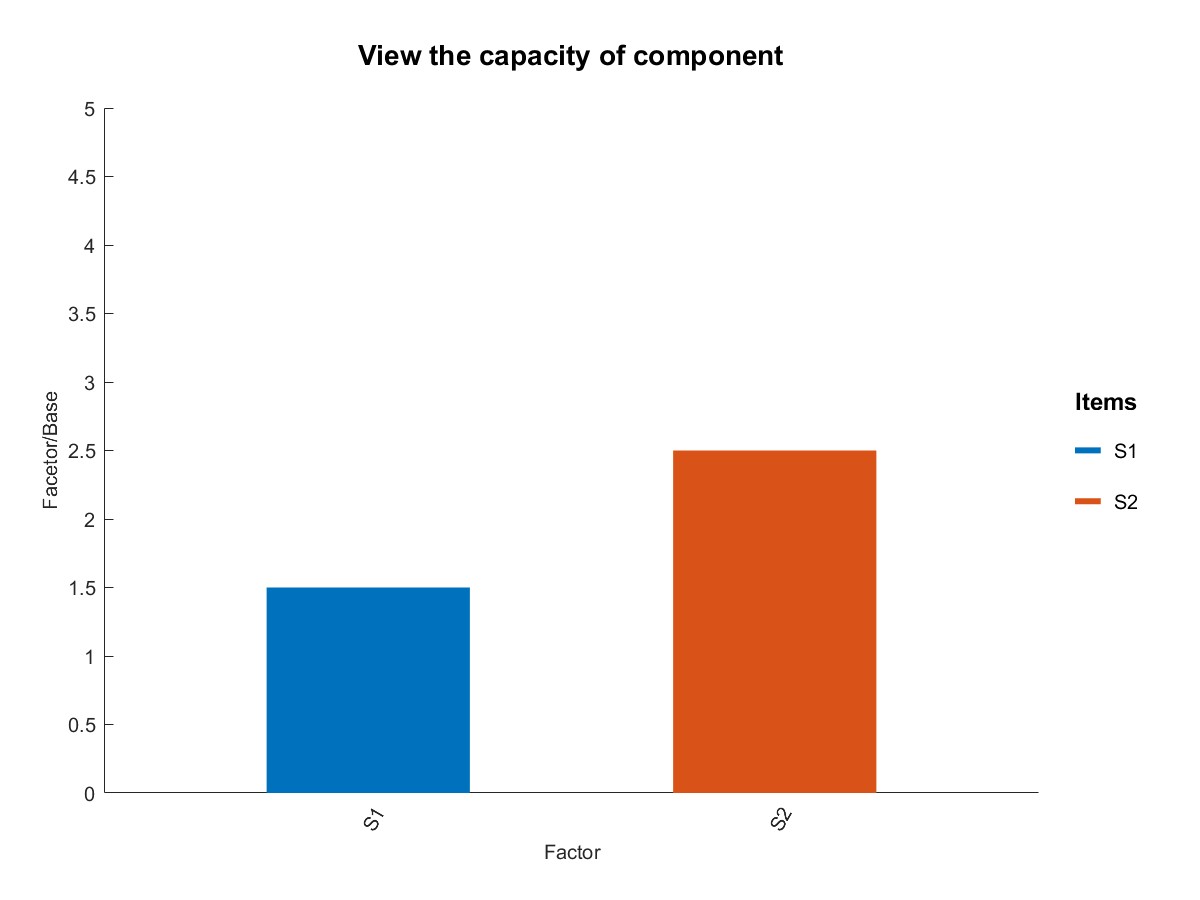
利用PlotCapacity()函数来检查部件的安全余量,此时我们看到S1的余量为1.5,表示该部件安全。
如果将S1的基准调整为4,此时S1的安全余量为0.75,该部件不安全。
baselineStruct.S1=2;
在Component下设置documentname,并将对应的文件放在Baffalo中的Document下,即可用Help函数打开对应的帮助文件。
参考文献
[1] JCSS PMC PART_I
[2] JCSS PMC PART_II
[3] JCSS PMC PART_III
[4] https://www.jcss-lc.org/jcss-probabilistic-model-code/
本网站基于Hexo 3-Hexz主题生成。如需转载请标注来源,如有错误请批评指正,欢迎邮件至 392176462@qq.com